5. Геометрический и аналитический способы сложения сил.

1.1. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ.

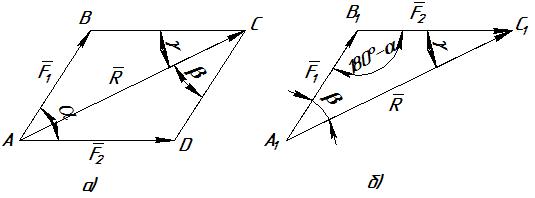
а) Сложение двух сил. Геометрическая сумма R двух сил F₁ и находится по правилу параллелограмма (рис. 1, а) или построением силового треугольника (рис. 1, 6), изображаю­щего одну из половин этого параллелограмма. Если угол между силами равен α, то мо­дуль R и углы β, γ , которые сила R образует со слагаемы­ми силами, определяются по формулам:

R = F₁ + F₂+2F₁F₂cosα,

или

F₁/sinγ =F₂/sinβ =R/sinα. (1)

Рис. 1

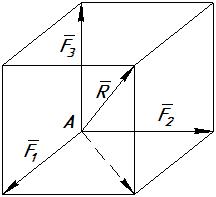
б) Сложение трех сил, не лежащих в одной плоскости.

Геометрическая сумма R трех сил F₁ F₂, F₃,

не лежащих в одной плоскости,

изображается диагональю параллелепипеда,

построенного на этих силах

(правило параллелепипеда).

Рис. 2

в) Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил может

б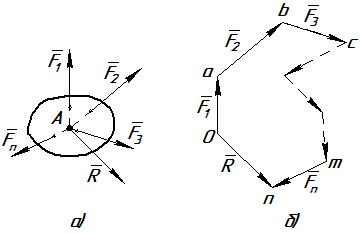 ыть найдена силового многоугольника.

Для нахождения этим способом суммы

сил (рис. 3, а), отклады-

ваем от произвольной точки О (рис. 3, б)

вектор Оа, изображающий в выбранном

масшта­бе силу F₁, от точки a - вектор ,

изображающий силу F₂, от точки b –

вектор , изображающий силу F₃, Рис. 3

и т. д.; от конца m предпоследнего вектора откладываем вектор , изображающий силу F_n.

Соединяя начало первого вектора с концом последнего, получаем

вектор , изображающий геометрическую сумму или главный вектор слагаемых сил:

или (2)

где k = 1, 2, 3, … , n.

1.2. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ

Aналитический метод решения задач статики основывается на понятии о проекции силы на ось. Проекция силы (как и любого дру­гого вектора) на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Если этот угол острый,- проекция положитель­на, если тупой,- отрицательна, а если сила перпендикулярна оси,- ее проекция на ось равна нулю.

Д ля аналитического задания силы необходимо выбрать систему коорди­натных осей Oxyz, по отношению к которой будет определяться направление силы в пространстве. Зная проекции силы F на координатные оси (f_х , F_y, F_z), можно опре­делить модуль силы и углы, которые она с образует координатными Рис. 4

осями,по формулам:

(3) (4)

Аналитический способ сложения сил заключается в том, что равнодействующая системы сил (главный вектор) находится через проекции сил на координатные оси:

(5)

Тогда (6)

(7)