12. Статистическое изучение вариаций. Показатели вариаций и методы их расчета.

Вариация – изминение изучаемого признака при переходе от одной единицы совокупности к др или от одного случая к др. Она необ-ма в качестве дополнения средних величин, средние величины дают обобщающую хар-ку совокупности по одному изучаемому признаку, но они не показывают пределы колебания данного признака. Сис-ма показателей вариации вкл след. эл-ты: Абсол.: 1.размах вариации – разность между наибольшим и наименьшим значении признаком в изучаемой сов-ти R=Xmax – Xmin. Он показ-т амплитуду колебаний изучаемого признака, гл. его достоинство – простота расчета. Но его использование ограничено, т к он не позволяет исследовать изминения признака внутри сов-ти; 2.среднее линейное отклонение – среднее знач. отклонений всех вариант от общей средней величины по данной сов-ти. Вычис-ся в 2-х формах: а) простая для не сгруппированных данных d=∑ (x- /n); б) взвешенная – для группировка d=∑ (x- )*f/∑f; 3.дисперсия – средний квадрат отклонений индивид-х знач. признака от общей средней. а) простая =∑ ( ; б) взвешенная =∑ ( /∑f. Не имеет размерности т.е в коэффициентах. 4.среднее квадратическое отклонение ; . Среднее квадрат-кое отклонение показывает абсолютную меру рассеивание признака у раз-х единиц изучаемой сов-ти. Относит. показатель: 5. Кооф. вариации – показ-т на сколько % в среднем все варианты отклоняются от обшей средней величины, показывает степень колебания признака V= *100. Совок-ть счит. однородной, если Кооф. вариации < 33%. Он широко испол. не только для сравнительной оценки вариации, но и для хар-ки однородности сов-ти.

13. Виды дисперсий и правила сложения дисперсий. Дисперсия-(от лат. рассеивание)- это средний квадрат отклонений индивидуальных значений признака от общей средней: 1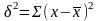 ; 2.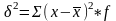 . Дисперсия не имеет размерности- это коэфф-т. Дисп. обл. след. математическими свойствами: 1.дисперсия постоянной величины=0; 2.если все варианты значений признака уменьшить на одно и тоже число, то дисперсия не уменьшится; 3.если все варианты значений признака уменьшить в одно и тоже число раз(k раз), то дисперсия уменьшится в 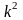раз. Виды дисперсий: *общая, *межгрупповая, *внутригупповая, *дисперсия альтернативного признака. Показатели вариации применяются так же для определения тесноты связи между группировочными и результативными признаками. На вариацию признака влияют случ. и систематические причины. Для определения влияния какого-либо фактора на величину вариации признака исп-ют аналитические группировки. Вариация, которая обусловлена влиянием группировочного признака наз. межгрупповой вариацией- она измеряется при помощи межгрупповой дисперсии(дисперсия групповых средних величин). Межгрупповая дисперсия хар-ет изменение групповых или частных средних по отношению к общей средней величине, она определяется: 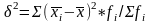, где 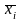- средняя величина групповая,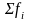 - сумма всех частот. Внутригрупповая дисперсия- для определения влияния всех факторов, кроме группировочного, вычисляют внутригрупповые дисперсии, а затем определяют среднюю из внутригрупповых дисперсий. Средняя из внутригрупповых дисперсий характеризует вариацию результативного признака, которая возникает под влиянием всех остальных факторов кроме группировочного. 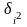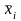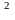Внутригрупповые, или частные, дисперсии определяются по формуле: =∑ (х - ) * f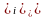 / f , где fi- веса признака x в соответствующей i-й группе. Средняя внутригрупповых, или частных, дисперсий определяется по формуле ср. арифм. взвеш. дисперсий групп: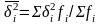 .В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой и ср. арифм. внутригрупповых дисперсий: 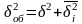.Отношение межгрупповой дисперсии к общей дает коэф-т детерминации 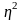, характеризующий долю вариации группировочного признака в общем объеме вариации, или на сколько процентов уровень результативного признака определяется группировочным признаком. Этот показатель обычно выражается в процентах: . 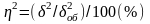Корень квадратный из этого же отношения наз.эмпирическим корреляционным отношением (η). Он характеризует тесноту связи между призн.

14. Понятия о рядах динамики, их виды и правила построения. Динамика- раз-тие яв-й и процессов во времени. Ряд динамики – ряд статис-их показ-лей, кот распол-ны в хронологич последова-ти. Каждый ряд вкл 2 эл-та: 1. моменты или периоды времени; 2.уровни ряда или стат показ-ли, кот хах-ют изуч-ый объект. В зав от способа регистрации данных раз-ют 2 вида рядов динамики. 1.Интервальные- их особенности: - показатели можно суммировать получая при этом новый ряд динамики с более длительным интервалом, - чем больше интервал, тем больше абсол-ый показ-ль интервального ряда. 2.Моментные ряды- его показ-ли суммировать нельзя. Ряды динамики могут состоять из абсол-ых, относ-ых и средних величин.

Аналит. показ. динамич. ряда

Анализ скорости и интенсивности разв. явления во времени осуществляется с помощью аналитических показателей, которые получаются в результате сравнения уровней ряда между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. Аналитические показатели динамики делятся на цепные, базисные или средние за весь рассматриваемый временной интервал.

Абсол.прирост—опр-ся как разность 2х уровней ряда(опр-ся по срав-ию с пост. и переем. базой –скорость роста):Δуб=уб-уо, Δуц=уi-уi-1; 2)темп роста—соот-е 2х уровней ряда (k-ах и %): Трб=уi/уo, Трц=уi/уi-1; 3)темп прироста—показ-т насколько % уровень отчетного периода будет больше или меньше уровня базис или предшед периода, для расчета исп-ся 2 приема: -исчис-ся как отн-е абсол. прироста к уровню базис. периода и умнож-ся на 100%; -исч-ся как разность между темпом прироста в % и 100%; 4)абсол. значение 1%прироста = деление абс. прироста на темп прироста, имеет смысл только с цепной базой - вычис-ся с точностью до 1тысяч; 5)средний абс. прирост—как средняя арифм-ая из пок-ей скорости роста за отдел. промеж-ки времени: Δу¯=∑∆уi/n-1, ∆у¯=уп-у1/п-1; 6)сред. темп роста (сред. геомет. вел-а) - опр-ся по срав-ю с пост и переем базой:Трб=n-1√ yn/yo;Трц=n √k1*k2*…kn; 7)сред. темп прироста—разность между сред. темпом роста в % и 100%.

Ср. абсолютный прирост:

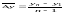
Ср. темп роста.

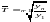
Ср. темп прироста.

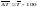
Ср. значение 1% прироста.