13. Вычисление коэффициентов и свободных членов канонических уравнений общим (кинематическим) методом.

Единичные перемещения δ_ik вычисляются пере­множением единичных эпюр M_i и M_k , грузовые ∆_iр - перемноже­нием эпюр Mi и M_p в основной системе метода сил.

Подобным же образом можно найти единичные и грузовые ре­акции в основной системе метода перемещений, однако здесь есть свои особенности.

Единичные реакции можно найти перемножением соответст­вующих единичных эпюр в основной системе:

(9.5)

Из формулы (9.5) следует, что главные коэффициенты rii все­гда положительны, а побочные коэффициенты rik (i 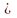k) могут иметь любой знак; в частности, они могут оказаться нулевыми.

Грузовые реакции. На первый взгляд, по аналогии с (9.5) гру­зовую реакцию Rip можно вычислить перемножением эпюр Mi и Mp в основной системе. Но эта аналогия оказывается ложной, так как результат перемножения этих эпюр равен нулю:

Можно доказать, что

(9.6)

где Mр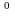 - эпюра изгибающих моментов от внешней нагрузки, построенная в любой системе, не содержащей i-ой дополнительной связи (как правило, в статически определимой, образованной из заданной отбрасыванием лишних связей).

14. Проверка коэффициентов и свободных членов канонических уравнений метода перемещений (единичных и грузовых реакций).

Формулы (9.5), (9.6) позволяют выполнить проверку правильности вычис­ления единичных и грузовых реакций.

Предварительно необходимо построить суммарную единичную эпюру 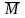Σ, сложив все единичные эпюры в основной системе:

(9.7)

Универсальная проверка. Результат умножения суммарной единичной эпюры (9.7) самой на себя должен быть равен алгеб­раической сумме всех единичных реакций. Докажем это:

(9.8)

Постолбцовая проверка. Правильность определения свобод­ных членов канонических

уравнений - грузовых реакций - про­веряют, умножая эпюру Σ на эпюру Mр от внешней нагрузки, построенную в статически определимой системе:

(9.9)

15. Определение внутренних усилий в рамах методом перемещений и их проверка. Алгоритм расчета.

На основании принципа суперпози­ции достаточно «собрать» результаты отдельных частных расчетов.

Таким образом, значения изгибающих моментов в заданной системе получаются по зависимости:

(9.10)

где k, Mp - изгибающие моменты в основной системе от еди­ничного перемещения k-ой дополнительной связи и от внешней нагрузки соответственно.

Изгибающие моменты в заданной системе, вычисленные по формуле (9.10), часто называют окончательными. В отличие от них, моменты, найденные ранее в основной системе, считаются промежуточными или вспомогательными. Единичные эпюры, ум­ноженные на соответствующие значения Z1; Z2,..., Zn , иногда называют «исправленными» эпюрами.

Определение поперечных и продольных сил. При расче­те рам и балок поперечные силы Q вычисляют по значениям из­гибающих моментов M, а продольные силы N - по значениям по­перечных сил. Для плоских рам удобно использо­вать следующие приемы. Поперечные силы Q могут быть найдены по значениям изги­бающих моментов M. Если эпюра M на участке стержневой сис­темы прямолинейна, удобно пользоваться дифференциальной зависимостью при изгибе

По этой зависимости, поперечная сила равна тангенсу угла на­клона прямолинейной эпюры моментов. Правило знаков следую­щее: сила Q считается положительной, если для совмещения оси стержня с эпюрой М ось необходимо вращать по часовой стрелке (рисунок 7.10).

Если эпюра M на участке непрямолинейна, поперечную силу удобно находить, вырезая участок и составляя для него уравнения равновесия.

Пусть, например, для рамы построена эпюра изгибающих мо­ментов (рисунок 7.11, а). Чтобы найти поперечные силы на уча­стке АВ, вырежем его и приложим к сечениям известные момен­ты и пока неизвестные силы (рисунок 7.11, б).

Моменты направляем так, как следует из эпюры изгибающих моментов М: эпюра построена на растянутых волокнах, значит, в сечениях А и В растянуты верхние волокна. Поперечные силы считаем положительными, т. е. они вращают рассматриваемый участок по часовой стрелке.

Составим уравнения моментов относительно точек А и В

По полученным значениям строим эпюру Q (см. рису­нок 7.11, б). В сечении с абсциссой где Q = 0, изгибающий мо­мент экстремален. Чтобы его найти, вырезаем участок длиной z0 (рисунок 7.11, в), из уравнения проекций на вертикальную ось Qa - qz0 = 0 определяем z0 = QA / q . Экстремальный момент нахо­дим из уравнения

Продольные силы N могут быть найдены по значениям попе­речных сил Q. Для этого необходимо отсечь отдельные стержни или вырезать узлы рамы, составить уравнения проекций на оси координат, из которых выразить искомые усилия.

Проверки правильности определения внутренних уси­лий. В методе сил проверкой правильности определения внутрен­них сил было соблюдение условий совместности деформаций в заданной системе (деформационная, или кинематическая провер­ка). В методе перемещений, напротив, эти условия автоматически выполняются при любых перемещениях узлов Zx, Z2, ..., Zn . Кри­терием правильности решения задачи является, очевидно, то, что внутренние усилия, вычисленные по данным перемещениям, удовлетворяют и всем условиям равновесия системы (статиче­ская проверка).

Фактически надо убедиться, что в условно введенных связях основной системы полные реакции равны нулю, т. е.

Для этого надо вырезать узлы и части конструкции и прове­рить, находятся ли они в равновесии под действием только внут­ренних усилий, приложенных в местах разрезов.

Проверка эпюры изгибающих моментов вычислением реакций связей. В п. 9.4.2 была получена формула (9.6) для определения реакции i-ой дополнительной связи, предполагающая перемноже­ние эпюр i и Mр . Здесь под Mр понимается эпюра от нагрузки в любой системе, не содержащей i-ой дополнительной связи. То есть, можно взять заданную статически неопределимую систему, в которой построена эпюра M от нагрузки. Тогда

Суммируя все грузовые реакции, получим

(9.11)

Условие (9.11) является необходимым и при верно построен­ных исходных единичных и грузовой эпюрах достаточным усло­вием правильности эпюры М.

Порядок расчета рам методом перемещений. Расчет ста­тически неопределимых рам, а также балок, работающих на из­гиб, удобно вести в следующем порядке:

1. вычисление степени кинематической неопределимости nK;

2. формирование основной системы;

3. составление системы канонических уравнений;

4. построение единичных и грузовой эпюр в основной системе;

5. вычисление единичных и грузовых реакций и их проверка;

6. решение системы канонических уравнений;

7. построение эпюры изгибающих моментов М и ее проверки;

8. построение эпюры поперечных сил Q (по готовой эпюре М);

9. построение эпюры продольных сил N (по готовой эпюре Q);

10. статическая проверка равновесия рамы в целом.