21. Основное нерав-во теории двойственности.

Для любых допустимых решений х(х₁,х₂,..х_n) и y(y₁,y₂,..y_n) прямой и двойственной задач ЛП справедливо нерав-во:

Док-во: ( )x_j = *. Эта сумма не изменится, если мы поменяем порядок суммирования: *= ( )y_j ; *

Малая теорема двойственности. Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них.

Теорема о достаточном условии оптимальности решений пары двойственных задач.

Если для некоторых допустимых решений х₀ и у₀ пары двойственных задач выполнено равенство: То данные решения являются оптимальными.

Экон.смысл: план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

22. Первая теорема двойственности.

Если одна из задач двойственной пары имеет оптимальное решение, то и др. имеет опт. решение, причем, экстремальные значения линейных форм в обеих задачах совпадают

Если же какая-то задача не имеет решения, то система ограничений др. задачи противоречива.

Экон.смысл: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения минимальных оценок ресурсов, причем цена продукта, полученного при реализации оптимального плана, совпадает с суммарной оценкой имеющихся ресурсов.

23. Вторая осн.Теорема двойственности

для того, чтобы допустимые решения х(х₁,х₂,..х_n) и y(y₁,y₂,..y_n) были оптимальными, необходимо и достаточно выполнение следующих условий

x⁰_j( ,

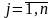
если какое-либо нер-во системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна быть равна 0. если же к.-л. Компонента оптимального решения положительна, то соотв-ее ей ограничение в двойственной задаче должно быть обращено в точное равенство.

Другими словами: 1)если х_j⁰>0,то a_ijy_i⁰=c_j; 2)если a_ijy_i⁰>c_j , то x_j⁰=0; 3)если y_i⁰>0, то a_ijx_j⁰=b_i; 4)если a_ijx_j⁰<b_i,то y_i⁰=0. j= , i=

Если по оптимальному плану расход i-того ресурса < его запасов, то оценка этого ресурса=0. если же оценка>0, то расход этого ресурса равен его запасу. Т.о. дефицитный (полностью используемый по оптимальному плану) ресурс имеет положит.оценку в двойственной задаче, а недефицитный – нулевую оценку.

С точки зрения пр-ва: если оценка ресурсов, расходуемых по j-ой технологии больше цены продукта, то j-ая технология не применяется (x_j=0). Если же по некот. Плану j-ая технология применяется (x_j>0), то оценка ресурсов, расходуемых по данной технологии, равна цене продукта.

24. Третья теорема двойственности.

Пусть имеются две пары двойств. Задач, и пусть в исходной задаче величины c_j и aij не меняются, а первые части системы ограничений меняются (b_i=var), тогда каждому вектору В=(b₁,b₂,..b_m), будет отвечать свое оптимальное решение исходной задачи.

Теорема: Значения переменных y_i⁰ в оптимальном решении двойственной задачи представляют собой оценки влияния правых частей b_i системы ограничений исходной задачи на величину максимума целевой функции: z_max/ b_i =y_i⁰ , при этом увеличение правой части i-го ограничения приводит к увелич. или уменьш. z_max в зависимости от того будет ли y_i⁰ положит. или отрицательным.

Экон.смысл: двойственная оценка ресурса – это приращение прибыли, приходящейся на единицу приращения этого ресурса.