36. Матричная игра типа m*n. Критерий оптимальности стратегий.

37. Теорема о преобразовании матрицы игры, сохраняющем оптимальные стратегии игроков.

38. Основная теорема теории игр, выражение оптимальных стратегий игроков через решения пары двойственных задач лп.

Математической моделью такого конфликта двух участников с противоположными интересами является игра с нулевой суммой. Участники это – игроки. Стратегия игрока – это выбор одного из множества возможных вариантов его действий. Рассмотрим конечные игры, в кот. множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока – от 1 до n. Если первый игрок выбрал свою i-ю стратегию, а второй игрок свою j-ю стратегию, то результатом такого совместного выбора будет платеж a_ij второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется платежной матрицей. Строки - соответствуют стратегиям первого игрока, столбцы -второго игрока. Игра происходит партиями.

а₁₁ а₂₁ а_1n

П= а₂₁ а₂₂ а_2n

а_m1 а_m2 а_mn

Смешанной стратегий первого игрока называется вектор P (p_1, p_2,…p_m ), где все p_{i 0} (i=1,2,…,m), а p =1. при этом p - вероятность, с которой первый игрок выбирает вою i-ю стратегию. Аналогично определяются смешанные стратегии и Q (q₁, q₂,…q_n)второго игрока. Чистая стратегия также попадает под определение смешанной – если все вероятности равны нулю, кроме одной, равной единице.

Если игроки применяют свои смешанные стратегии P (p_1, p_2,…p_m ) и Q (q₁, q₂,…q_n) соответственно, Выигрыш первого: выигрыш a_ij

Вероятность p_i q_j.

То есть первый игрок с вероятностью p_i g_j. выигрывает a_ij.. Математическое ожидание выигрыша первого игрока равно М(P,Q)= p_i q_j a_ij есть средний выигрыш. И это равно математическому ожиданию проигрыша второго игрока. Если игроки озабочены только максимизацией среднего дохода за партию игры то они будут играть со своими оптимальными стратегиями: – Первый игрок и – второй, оптимальны стратегии если М(P,Q*) М(P*,Q*) М(P*,Q)

Математическое ожидание с. в. называется ценой игры, обозначим ее .

Строка k доминирует над строкой i, если все элементы строки k не меньше соответствующих элементов строки i и хотя бы один строго больше. Доминируемую строку можно временно удалить, потому что в оптимальной стратегии ей будет соответствовать вероятность ноль. Столбец l доминирует над столбцом j, если все его элементы не больше соответствующих элементов столбца j, а хотя бы один строго меньше.

Доминируемый столбец j можно временно удалить, т.к. в оптимальной стратегии 2-го игрока ей будет соответствовать вероятность ноль.

Основная теорема теории матричных игр:

В матричной игре с нулевой суммой у игроков есть оптимальные стратегии.

Другими словами: Всякая матричная игра имеет седловую точку в смешанных стратегиях.

39. Игры с природой: основные понятия, матрицы рисков, критерии Вальда, Севиджа, Гурвица.

Предположим, что лицо, принимающее решения может выбрать одну из возможных решений 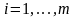. Ситуация является неопределенной, понятно лишь, что наличествует какой-то из вариантов .

Если будет принято 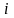-e решение, а состояние внешней среды соответствует -й ситуации, то фирма, возглавляемая ЛПР, получит доход . Матрица называется матрицей последствий (возможных решений).

Неопределенная ситуация похожа на матричную игру, отличие состоит в том, что противником в данном случае является природа, цели которой не всегда противоположны нашим: они могут совпадать с целями ЛПР, а могут и не совпадать. Поэтому ситуация с неопределенностью называют еще играми с природой.

В ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме?

Допустим, мы хотим оценить риск, который несет -e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть -я , то было бы принято решение, дающее доход .

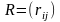Значит, принимая -e решение мы рискуем получить не , а только , значит принятие -го решения несет риск недобрать . Матрица называется матрицей рисков.

Более широкое понятие – неопределенность. Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации.

Правило Вальда (крайнего пессимизма): рекомендует принять такое решение i₀ , что 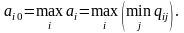Правило Сэвиджа (правило минимального риска): анализируется матрица рисков . Рекомендует принять решение 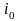, такое что

Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение , на котором достигается максимум где . Значение выбирается из субъективных соображений.