27. Доказать один из признаков подобия треугольников.

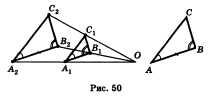Первый признак подобия треугольников: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Второй признак подобия треугольников: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

Третий признак подобия треугольников: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

А] Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны .

28. Значение синуса, косинуса и тангенса некоторых углов (без доказательства).

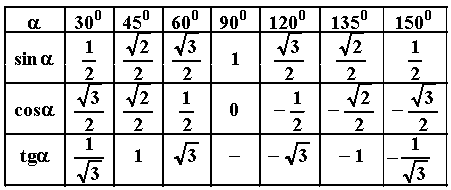
29. Доказать один из признаков подобия прямоугольных треугольников.

Первый признак подобия треугольников.

Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

Доказательство. Начало доказательства одинаково для всех трех признаков. Рассмотрим два треугольника ABC и A1B1C1, для которых выполняется одно из трех сформулированных условий (рис. 1). Причем будем считать, то обозначения выбраны следующим образом.

Первый признак. Равны углы при вершинах A и A1, кроме того,

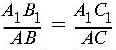
Отложим на луче AB отрезок AB2 = A1B1 и проведем через B2 прямую, параллельную BC. Получившийся треугольник AB2C2 подобен треугольнику ABC по основной теореме о подобных треугольниках.

Нам остается доказать, то треугольник AB2C2 равен треугольнику A1B1C1 .

Первый признак. В треугольниках A1B1C1 и AB2C2 равны углы при вершинах A и A1, A1B1 = AB2 . Кроме того, по условию, а из того, то треугольники AB2C2 и ABC подобны, следует равенство. Из этих двух равенств получаем (так как A1B1 = AB2), то A1C1 = AC2. Значит, треугольники A1B1C1 и AB2C2 равны по первому признаку равенства треугольников.

30. Формулы координат середины отрезка и расстояния между двумя точками на плоскости (без доказательства).

Формула расстояния между двумя точками

Пусть A и B -- две точки плоскости, координаты которых в декартовой системе координат: (x1; y1) и (x2; y2), тогда

Формула

Строгая формулировка

Координаты середины отрезка с концами

и

находятся по формуле:

- координаты точки ;

- координаты точки

в декартовой системе координат на плоскости

31. Доказать теорему Пифагора.

b2 = a2 + c2

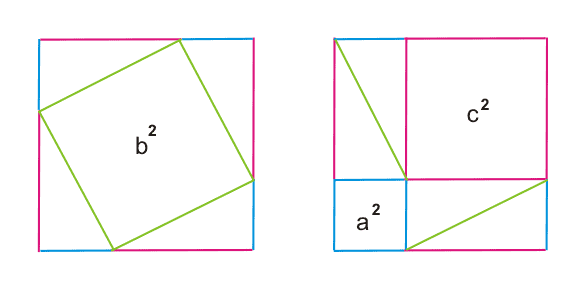
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.

В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.

Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.