Доказать теорему о свойстве касательной к окружности.
Теорема о свойстве касательной к окружности
Теорема. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Дано: окр (О; ОА)
P – Касательная к окружности,
А – точка касания.
Доказать: P перпендикулярна ОА.
Доказательство (методом от противного)
Предположим, что P не перпендикулярна ОА
В этом случае радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведённый из точки О к прямой Р, меньше наклонной ОА, то расстояние от центра О окружности до прямой Р меньше радиуса. Следовательно, прямая Р. и окружность имеют две общие точки, т.е. Р – секущая. Но это противоречит условию теоремы, что Р. - касательная к окружности. Так как получили противоречие, то предположение, что Р не перпендикулярно ОА было неверным, значит, Р. перпендикулярна ОА. Итак, касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Ч.т.д.
Верна и теорема, обратная теореме о свойстве касательной - признак касательной.
Теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Дано: окр (О;ОА), Р, А принадлежит Р, Р перпендикулярна ОА
Доказать: Р. – касательная к окр (О;ОА).
Доказательство
По условию Р принадлежит ОА, ОА – радиус окружности, поэтому расстояние от центра окружности до прямой Р равно радиусу ОА. Следовательно, прямая и окружность имеют только одну общую точку. А это означает, что данная прямая Р является касательной к окружности. Итак, если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. Ч.т.д.
Замечательные точки треугольника (без доказательства).
Замечательными точками треугольника являются
Точки пересечения:
Медиан — центроид, центр масс;
Биссектрис — инцентр, центр вписанной окружности;
Высот — ортоцентр;
Серединных перпендикуляров — центр описанной окружности;
Cимедиан — точка Лемуана;
Биссектрис серединого треугольника (его инцентра) — точка Шпикера;
Точки пересечения отрезков, соединяющих вершины треугольника:
c точками касания противоположных сторон и вписанной окружности — точка Жергонна;
c точками касания противоположных сторон и вневписанной окружности — точка Нагеля;
c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника (наружу) — первая точка Торичелли
с соответствующими свободными вершинами правильных треугольников, построенных внутрь треугольника — вторая точка Торичелли.
c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара;
Центр окружности девяти точек.
Центральный угол. Вписанный угол. Доказать теорему об измерении вписанного угла.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°.
Доказательство
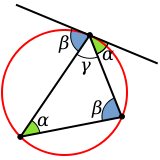
Через вершину треугольника проведена касательная к описанной окружности
Следствия:
Через вершину треугольника проведена касательная к описанной окружности
Вписанные углы, опирающиеся на одну дугу, равны.
Угол, опирающийся на диаметр, — прямой.
Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности.
Угол между касательной и хордой является предельным случаем вписанного угла и также равен половине дуги, на которую опирается.
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.