17. Трапеция. Виды трапеции. Доказать теорему о средней линии трапеции.

Трапеция – четырехугольник, у которого только две противолежащие стороны параллельны.

Виды трапеции: прямоугольная, равнобедренная (равнобокая), разнобокая.

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема о средней линии трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Д-ть:

EF || AB, EF || CD; EF= (AB + CD).

Д-во:

A E = ED (теор. Фалеса)

BF = FC

EF- ср. линия.

EF || AB; EF || DC

EO = AB; OF = DC.

EF = EO + OF = (AB + CD).

18. Параллельный перенос. Свойства параллельного переноса.

Параллельный перенос фигуры Ф называется такое преобразование фигуры Ф, при котором все ее точки смещаются в одном и том же направлении на одно и то же расстояние.

Свойства параллельного переноса в пространстве.

• Параллельный перенос есть движение.

• При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую.

• При параллельном переносе плоскость переходит либо в себя, либо в параллельную ей плоскость.

• Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки   и  , существует единственный параллельный перенос, при котором точка   переходит в точку  .

19. Доказать теорему Фалеса.

Теорема.  Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. 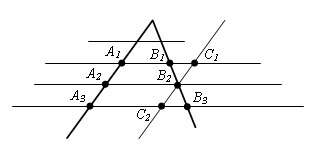   Доказательство.  Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.  Проведем через точку В2 прямую С1С2, параллельную прямой A1A2. Получаем параллелограммы A1C1B2A2 и A2B2C2A3. По свойствам параллелограмма, A1A2 = C1B2 и A2A3 = B2C2. Так как A1A2 = A2A3, то C1B2 = B2C2.  Δ C1B2B1 = Δ C2B2B3 по второму признаку равенства треугольников (C1B2 = B2C2, C1B2B1 = C2B2B3, как вертикальные, B1C1B2 = B3C2B2, как внутренние накрест лежащие при прямых B1C1 и C2B3 и секущей С1С2). Из равенства треугольников следует, что B1B2=B2B3. Теорема доказана.

20. Гомотетия. Свойства гомотетии.

Гомотетия с центром в точке О и коэффициентом k 0 называется такое преобразование, при котором каждая точка М отображается в такую точку М1, что выполняется равенство:

Свойства.

• Если коэффициент гомотетии равен 1, то гомотетия является тождественным преобразованием: образ каждой точки совпадает с ней самой.

• Если коэффициент гомотетии равен -1, то гомотетия является центральной симметрией.

• Как и любое преобразование подобия, гомотетия преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.

• Как и любое преобразование подобия, гомотетия сохраняет величины углов между кривыми.