Общие свойства

• Центральная симметрия является движением (изометрией).

• В n-мерном пространстве центральную симметрию можно представить как композицию n последовательных отражений относительно n взаимно перпендикулярныхгиперплоскостей, проходящих через центр симметрии. В частности

• В чётномерных пространствах центральная симметрия сохраняет ориентацию, а в нечётномерных — не сохраняет.

• Центральную симметрию можно представить также как гомотетию с центром A и коэффициентом −1 ( ).

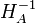• Композиция двух центральных симметрий — параллельный перенос на удвоенный вектор из первого центра во второй:

Изоме́три́я, или движе́ние, или (реже) наложе́ние — биекция (преобразование), которая сохраняет расстояние между соответствующими точками, то есть если   и   — образы точек   и  , то  .

11. Д оказать теорему о сумме внутренних углов многоугольника.

Теорема. Сумма углов выпуклого n-угольника равна 180 (n-2).

Доказательство. Пусть дан выпуклый многоугольник А₁А₂А₃…А_n.

Данный n-угольник диагоналями, выходящими из одной вершины

делится на (n – 2) треугольника так, как показано на рис.

Сумма углов многоугольника состоит из суммы углов всех треугольников.

Сумма углов каждого треугольника равна 180 . Поэтому сумма углов многоугольника равна 180 (n - 2). Ч.т.д.

Следствие. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360 .

Сумма внутреннего и внешнего углов при каждой вершине n-угольника составляет 180 . Следовательно, сумма всех внутренних и внешних углов n-угольника равна 180 n.

Поэтому сумма внешних углов n-угольника будет равна:

180 n - 180 (n – 2) = 360 .

Значит, сумма внешних углов n-угольниками не зависит от числа n.

12. Формулы площади треугольника, прямоугольного треугольника (без доказательства).

Любой :

Где a, b, c – стороны,

, где R – радиус описанной окружности.

, где , где r – радиус вписанной окружности.

Равнобедренный :

Прямоугольный :

Равносторонний :

Прямоугольный равнобедренный :

13. Ромб. Доказать основные свойства ромба.

Ромб – параллелограмм, у которого все стороны равны.

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Теорема. Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.

Доказательство. Пусть дан ромб ABCD, в котором AC и BD являются его диагоналями.

Докажем, что AC BD и 1= 2.

На основании свойства параллелограмма имеем: AO=OC. Треугольник ACD равнобедренный, поэтому отрезок DO является в нем биссектрисой и высотой, т.е. DO AC или AC BD и 1= 2. Аналогично доказывается, что 5= 6. Ч.т.д.