13. Степеневі ряди

Озн. Степеневим рядом називається функціональний ряд виду

(1) або

(2)

Де

Зазначимо що заміною t= степеневий ряд (2) перетворюється у ряд (1), тому подальше твердження будемо формувати для рядків (1). Крім того область збіжності степеневого ряду завжди не пуста. Для ряду (1) вона містить принаймні одну точку х=0

Теорема 1 (Абеля)

Якщо степеневий ряд (1) збігається у точці , то він абсолютно збіжний ∀х таких що | |<| |. Якщо ряд (1) розбіжний у точці , то він розбігається ∀х таких що| |>| |.

Із теореми Абеля випливає, що для степеневих рядів можливі лише 3 випадки області збіжності:

1) область збіжності ряду (1) складається із однієї точки х=0

2) степеневий ряд (1) збігається ∀х∈R

3) ∃ таке число R>0що ряд (1) збіжний ∀х таких що |x|<R і розбіжний ∀х таких що |x|>R

Теорема2

Радіус збіжності степеневого ряду можна знайти за формулою

або

Зауваження: слід звернути особливу увагу на те, що теорема у межових точка інтервалу збіжності в цих точках степеневий ряд (1) може бути як збіжним так і розбіжним і для кожного конкретного ряду необхідні окремі дослідження його поведінки у межових точках

Схема дослідження області збіжності степеневого ряду

1. За формулою знаходимо радіус збіжності

2)Вказуємо інтервал збіжності для: Ряду (1) (- R,R) , Ряду (2) ( )

3) досліджуємо поведінку степеневого ряду у межових точках інтервалу збіжності

4) Точки в яких відповідні числові ряди збігаються приєднуємо до інтегралу збіжності

З теореми Абеля і властивостей рівномірно збіжних функціон. рядів випливають наступні властивості степеневих рядів

1. збігається абсолютно і рівномірно на ∀ відрізку [-ρ, ρ) що міститься в інтервалі збіжності (-R,R)

2. Сума степеневого ряду (1) неперервне в середині його інтервалу збіжності

3. Якщо менші інтеграли α і β знаходяться в середині інтегралу збіжності (-R,R) то степеневий ряд (1) можна почленно інтегрувати на відрізку [α, β).

4. Степеневий ряд (1) можна почленно диференціювати на інтервалі (-R,R) при цьому одержаний ряд має той самий інтервал збіжності що й вихідний ряд (1)

Із властивості 3 і 4 випливає дуже важливий у подальшому наслідок на відрізку [0,Х] де |x|<R степеневий ряд (1) можна скільки завгодно раз інтегрувати і диференціювати.

При цьому одержані ряди будуть мати той самий інтервал збіжності, щол і ряд (1)

14. Ряд Тейлора

Нехай f(x) є сумою степ. ряду (1) на (-R, R). Вираз (1) наз. також розкладанням ф-ції f(x) в околі точки або розкладання ф-ції за степенями _. Числа наз. коефіціентами цього розкладую Задача полягає в тому щоб у дифірінціальному ряді (1) знайти коефіцієнти розкладання. За властивістю степеневих рядів, ряд (1) можна дифірінціювати скільки завгодно раз і одержані в результаті цього ряди будуть мати інтервали збіжності

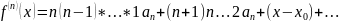
Звідси одержимо … ,

Підставляючи знайдені коефіцієнти в (1) одержимо степеневий ряд (2).

Опр. Ряд (2) наз. рядом Тейлора ф-ції f(x).

Теорема 1: Якщо ф-ція f(x) на подана у вигляді степ. Ряду (1), то це подання єдине і даний степ. ряд є рядом Тейлора ф-ції f(x).

Виявляється, що у випадку коли ф-ція f(x) нескінченно раз дифірінційовна на , її ряд Тейлора (2) зовсім не обов’язково буде збігатися до ф-ції f(x), для якої він формально був не будований. Цей ряд (2) взагалі може збігатися зовсім до іншої ф-ції. Виникає питання: за яких умов ряд Тейлора (2) ф-ції f(x) збігається саме до f(x) існує декілька тверджень в яких розглядаються такі умови. На практиці частіше користуються наступною теоремою.

Теорема 2 Нехай ф-ція f(x) має похідну будь-якого порядку на і таке що n=0,1,2,3.. і виконується нерівність .

Озн. Рядом Маклорена наз. ряд Тейлора (2), якщо :