9.Числові ряди. Найпростіші властивості.

Озн. : Нехай задана посл-ть дійсних чисел {a_n}^∞_n=1={a₁,a₂,…., a_n ….}.

Числовим рядом наз-ся вираз a₁,a₂,…., a_n …= .(1)

Цьому ми не приписуємо ніякого числа, тому що не можна виконати нескінченну суму.a_nназ. загальним членом ряду (1)_.

Частинною сумою ряду (1) наз. вираз S_n a₁+a₂+., +a_n

Сумою ряду (1) наз. S = lim S_n якщо ця границя існує.

^n->∞

Ряд 1 наз. збіжним, якщо сума S –скінченне число, тоді пишуть = S

Якщо ця границя є нескінченна або не існує ряд 1 наз. розбіжним. Це позначають = 

Якщо ряд збігається і має скінченну суму S , то ряд с також збігається і має суму СS

Дов-ня:

Нехай S_n= ,_n= _С=сS_n. частинні суми відповідних рядів. Тоді за озн. суми ряду

lim_n σ_n= lim_{n C} = Clim_n = lim_n S_n =сS.

2)Якщо ряди і збіг-ся і мають суми А і В то збіжн-ми єтакож ряди =А В.

Дов-ня:

Нехай S_n= , _n=

S*_n= , S*_n= S_n _n

Тоді lim_n S_n=А , lim_n _n=В.

3)На збіжність не впливає приєднання до нього або відкидання скінченної кількості членів

Нехай числовий ряд з якого відкинемо m членів суму яких позначимо _m Візьмемо n настільки великим щоб всі відкинуті доданки містились у частинній сумі S_n. Через С_n-m позначемо ті доданки, що містяться в S_n і не містяться в _m тоді

S_n= с_m+_n-m тоді lim_n S_n= с_m+ lim_n _n-n.

Звідси випливає що границі у лівій і правій частині одночасно існують або не існують тобто ряд один збіжний(розб-й) коли збіжн-й(розб-й) ряд без m його членів.

Озн: Вираз r_n = наз. залишком ряду (1).

Із властивості (3) випливає, що ряд 1 збіжний(розбіжний) тоді і тільки тоді, коли збіжним(розбіжним) буде його залишок.

4) якщо ряд 1 збіжний, то lim_n r_{n =} 0

Доведення:

=S < 

за озн. S_n + r_n = Sr_n = S- S_n

тоді lim_n r_n = lim_n (S- S_n)= S- S=0

5)Необхідна умова збіжності .

Якщо ряд 1 збіг-ся то lim_n а_n=0.

Дов-ня:

Нехай = S< тоді a_n = S_n - S_n-1= - ^-1=> lim_n a_n= lim_n( S_n - S_n-1)=S- S=0

Зауваж. Наведена умова є лише необхідною але не достатньою тобто існують розбіжні де lim_n а_n =0

_

10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.

О-я: Числовий ряд - наз-ся знакододатнім або додатнім, якщо а_n, n

Аналогічно модна розглянути означення відємного ряду.

Заув-я:

З властивості 1 числових рядів випливає, що дослідження відємного ряду одразу можна звести до дослідження відповідного додатньного ряду, якщо винести мінус за знак суми.

Тому надалі розглядатимемо лише додатні ряди.

Теорема1(ознаки порівняння)

Нехай і - додатні ряди і для n викон-ся нер-ть 0 а_n b_n (1) то із збіжності ряду (2) випливає збіжність (3) ,а розбіжності 3 випливає розб-ть 2.

Враховуючи властивість (3) теорема 1 працює і у тому випадку, якщо нерівність (3)виконується не для всіх n, а починаючи з деякого . При застосуванні цієї ознаки на практиці частіше частіше всього досліджуваний ряд порівнюють з рядами, збіжність або розбіжність яких вже відома. До них відносяться: геометрична прогресія

Узагальнений гармонічний ряд: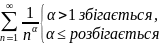 Поведінку цього ряду при α≠1 розглянемо далі.

Т-ма2(гранична ознака порівняння)

Якщо задані 2 додатні числові ряда (1) , (2) існує границя lim_n а_n/b_n=к, де 0<к<+, то ряди (1) і (2) збігаються або розбігаються одночасно, тобто мають однакову поведінку.

Теорема 3 (ознака Д’аламбера):Нехай задано додатній числовий ряд (1). Якщо і q, то ряд (1) збіжний, q - ряд (1) розбіжний.

Теорема 4 (ознака Коши): Нехай для додатного ряду існує границя , тоді якщо 0≤q даний ряд збіжний, q - ряд розбіжний.

Зауваження: Ознаки Д’аламбера і Коши рівносильні у тому розумінні, що коли 1 з цих ознак не дає відповіді на питання про збіжність (q=1), то інша ознака теж дає q=1. Для дослідження питання про збіжність або розбіжність ряду в цьому випадку застосовують інші ознаки.

Теорема5 (Інтегральна ознака): Нехай задано числовий ряд (1), члени якого є значеннями неперервної додатної і монотонноспадної ф-ї f(x) на [1,+), тоді ряд (1) збігається, якщо збігається невласний інтеграл 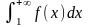, і ряд (1) розбігається, якщо цей інтеграл розбіжний.

Теорема6: (ознака Раабе)

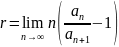Якщо – додатній числовий ряд і , то коли r>1 ряд збігається, а коли r<1 ряд розбігається.