4. Повний диференціал функції багатьох змінних. Диференціали вищих порядків.

Нагадаємо, що ф-я z = f(x,y) диференційована в точці М. Тоді, за означенням, її повний приріст в цій точці можна надати у вигляді z=Ах+Ву+x+y (1), де А,В – сталі (дійсні числа, які не залежать від х,у); х,у), х,у) – нескінченно малі ф-ї, якщо х, у0.

Означення: Повним диференціалом dz, диференційованої в точці М(х,у) ф-ї z = f(М) називають головну, лінійну відносно х,у, частину повного приросту (1) цієї ф-ї в т. М. Тобто, за означенням dz=Ах+Ву (2).

За теоремою про існування частинних похідних диференційованої ф-ї A = dz / dx, B = dz / dy. Крім того будемо вважати, що для незалежних змінних х та у прирости цих змінних dх=х, dу=у. Тоді враховуючи це, формулу (2) можна записати 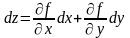(3). Якщо наприклад функція залежить від більшого числа змінних u = f (x,y,z), то її повний диференціал

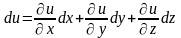
Теорема: Різниця між повним приростом z і повним диференціалом dz є нескінченно мала вищого порядку при х, у0 у порівнянні з  = (х²+у²)^1/2.

Доведення: З формул (1) і (2) маємо

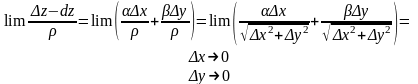
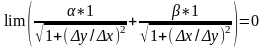, оскільки ф-ї  і  - нескінченно малі ф-ї при х, у0, а ф-ї х/, у/ – обмежені. х/(х²+у²)^1/2)=1/(1+(у²/х²)1, оскільки у²/х²1 х/1; у/1 аналогічно.

Зауваження: наведена теорема дозволяє стверджувати, що при досить малих х, у виконується наближена рівність: zdz, або f(х+х,у+у) - f(x,y)  (z/х)х+ (z/у)у . З останнього виразу одержимо формулу, яка широко використовується в наближених обчисленнях значень ф-й багатьох змінних, оскільки диференціал ф-ї обчислюється простіше ніж повний приріст: f(х+х,у+у)  f(x,y) + (z/х)х+ (z/у)у

Означення: Диференціалом 2 порядку ф-ї z = f(x,y) називається диференціал від диференціала першого порядку цієї функції і визначається як d²z = d(dz).

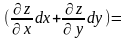
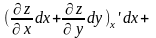
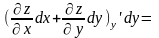
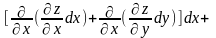
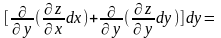
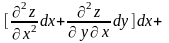
Нехай ф-я z = f(x,y) має неперервні мішані похідні, знайдемо формулу для диференціала 2 порядку цієї ф-ї. d²z = d(dz) = iз (3) =d 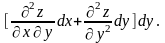(4). Символічно (4) можна записати так: d²z=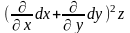 . Аналогічно можна довести d³z=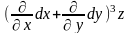 (5). Застосовуючи метод математичної індукції одержимо формулу для диференціала n порядку dⁿz= , де dⁿz=d(d^n-1z) (6).

Зауваження: Формули (4-6) справедливі лише у випадку коли змінні х,у ф-ї z = f(x,y) є незалежними.

5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.

Нехай z=f(x,y) ф-я 2 змінних х, у, кожна з яких, в свою чергу ф-я незалежної змінної t (x=x(t), y=y(t)), тоді z=f(x(t),y(t)) є складна ф-я змінної t.

Теорема 1: Нехай ф-ї x=x(t), y=y(t) диференційовані у т. М₁ (t), а ф-я z=f(x,y) диференційована у відповідній точці М₂ (х,у), тоді складна ф-я z=f(x(t),y(t)) диференційована в т. М₁ (t) і її похідну можна знайти за формулою: 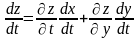(1).

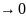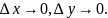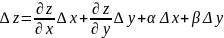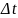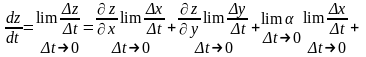
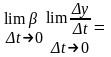
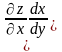
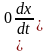
Доведення: За умовою теореми x=x(t), y=y(t) диференційовані ф-ї, а отже і неперервні. Тоді, якщо t , то і За умовою функція z=f(x,y) диференційована. Це означає, що її повний приріст: (2) де ,  – нескінченно малі ф-ї, якщо х, у0. Поділимо обидві частини рівності (2) на і перейдемо в одержаному виразі до границі, при t : 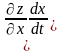. Звідси одразу випливає рівність (1).

Наведену теорему можна узагальнити на випадок більшого числа змінних. Якщо 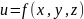, де x=x(t), y=y(t), z = z(t), то похідна ;

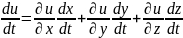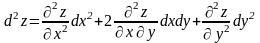
Теорема 2: Якщо ф-ї x=x(u,v), y=y(u,v) диференційовані у т. М₁(u,v), а ф-я z=f(x,y) диференційована у відповідній т. М₂(х,у), тоді складена ф-я z=f(x(u,v),y(u,v)) диференційована у т. М₁(u,v) і її частинні похідні можна знайти за формулами:

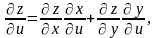
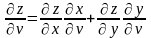(3). Доводиться аналогічно попередній.

Розглянемо диференціал складної ф-ї: dz=(z/u) d u+(z/ v) d v = за (3) = (z/х*х/u+z/у*y/u)du + (z/х*х/ v+z/у*у/v)dv = z/х((х/u)du+(х/ v) d v) + z/у((y/u) d u+(у/v) d v)= (z/х) dx+ (z/у) dy (4). Тобто dz = (z/х) dx+ (z/у) dy.

Порівнюючи (4) з формулою повного диф-а ф-ї z=f(x,y), одержимо що перший диф-л dz ф-ї z=f(x,y) має незмінну і інваріантну форму незалежно від того чи є змінні х,у незалежними зм-ми , чи х,у – ф-ї від змінних u,v. Заув-ня: Диф-ли вищих порядків не мають властивості інваріантності. Приклад: z=f(x,y), х=х(u,v), у=у(u,v)

²z= dz(dz)= d((z/х)dx +(z/у)dy)= (²z/х²)dx² +2(²z/(ху))dxdy+(²z/у²) dy²+(z/х) d²х + (z/у) d²у (5).

Порівнюючи ф-лу (5) із відповідною ф-ю для d²z у випадку незалежних змінних, бачимо, що вони суттєво різні, тобто інваріантності немає.