17.Число ударов молекул газа о стенку.

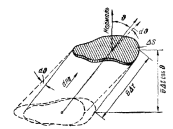
Рассмотрим идеальный одноатомный газ, находящийся в равновесии в сосуде объемом V. Выделим молекулы, имеющие скорость от v до v + dv. Тогда число молекул, движущихся в направлении углов q и f с этими скоростями будет равно: dNv,q,f = dNv·dW/4p. Выделим элементарную поверхность площадью dП., которую примем за часть стенки сосуда. За единицу времени до этой площади дойдут молекулы, заключенные в косом цилиндре с основанием dП и высотой v·cos q ( см. рис. 14.3). Число пересечений выбранными нами молекулами выделенной поверхности (число ударов о стенку) в единицу времени dnv,q,f будет равно произведению концентрации молекул на объем этого косого цилиндра: dn(v,q,f) = dП·v·cos q·dNv,q,f/V, где V - объем сосуда, в котором содержится газ. Проинтегрировав выражение по углам в пределах телесного угла 2p, что соответствует изменению углов q и f в диапазоне от 0 до p/2 и от 0 до 2p соответственно, получим формулу для расчета полного числа ударов молекул, имеющих скорости от v до v + dv о стенку. (2) . Проинтегрировав выражение по всем скоростям получим, что число ударов молекул о стенку площадью dП в единицу времени будет равно(2):. Учитывая определение средней скорости получим, что число ударов молекул о стенку единичной площади в единицу времени будет равно:

n = N/V·<v>/4 = n·<v>/4.

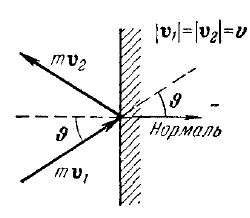
18.Газокинетический вывод выражения для давления газа на стенку.

При абсолютно упругом ударе о стенку сосуда молекулы массы m, движущейся под углом q со скоростью v к ее нормали, импульс молекулы изменится на величину dp, равную dp = - 2m·v cos q. Импульс стенки при этом изменится на противоположную по знаку величину. В соответствии со вторым законом Ньютона скорость изменения импульса стенки равна силе, с которой молекула на нее подействовала. В свою очередь, отношение нормальной составляющей силы к площади- есть давление на стенку. Следовательно, dP = dp·dnv,q,f = dp·v·cos q·dNv,q,f/V. Подставив и проведя интегрирование по углам и скоростям, получим, что давление P оказываемое всеми молекулами на стенку, равно: , где dPv - давление, создаваемое молекулами, имеющими скорость v, равное

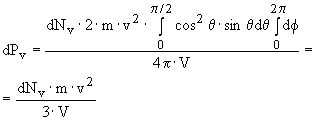
19.Функция распределения вероятностей. Ее свойства.

Функция статистического распределения— плотность вероятности в фазовом пространстве. Знание функции распределения полностью определяет вероятностные свойства рассматриваемой системы. P_i=lim_N®¥N_i/N – вероятность появления результата x_i, при N – кол-во значений х, N_i – кол-во измерений. Возьмем величину а (а – очень мала, скажем а=10^-6), найдем число измерений DN₀, при которых 0<x<a; DN_i при которых a<x<2a…DN_x при которых результат измерений от х до х+а и т.д. DP₀=DN₀/N – вероятность того что результат окажется от 0 до а. DP₁=DN₁/N и т.д. Возьмем ось Х (1) и отложим на ней полоски, шириной а и высотой DP_x/a. Такая диаграмма назыв. гистограммой вероятности. Площадь гистограммы равна 1. Если a®0 то получим (2); f(x), определяющая аналитически гистограмму при а®0 назыв. ф-ей распределения вероятностей. S столбика. шириной dx (2) равна вероятности того что результат измерений окажется в пределах от x до x+dx. Обозначим эту вероятность dP_x: dP_x=f(x)dx. Площадь под f(x)=1 Þ òf(x)dx=òdP_x=1.(*)

1) Свойства:Значения функции распределения принадлежат отрезку [0, 1]. 2) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале. 3) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице. 4) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.