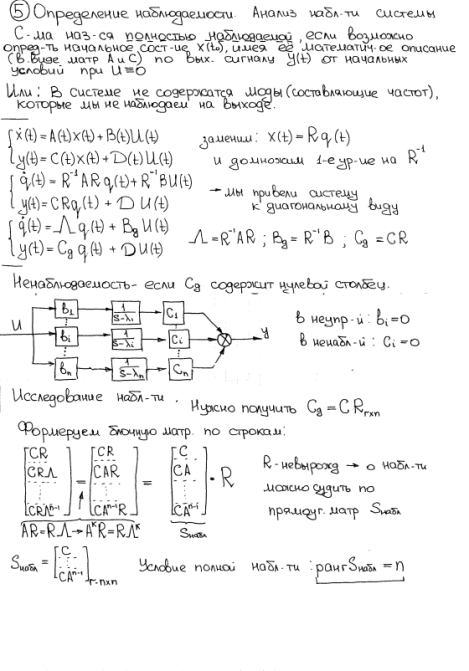
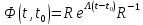1.1) Переходная матрица. Методы ее нахождения и ее свойства.

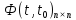– переходная матрица, матрица перехода из одного состояния в другое.

Она должна удовлетворять решению однородной системы:

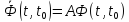
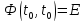
Для нестационарной системы:

t1>t0:x(t1)=Ф(t1,t0)*x(t0)

t2>t1:x(t2)=Ф(t2,t0)*x(t0)

x(t2)= Ф(t2,t1)*x(t1)= Ф(t2,t1)* Ф(t1,t0)*x(t0) => Ф(t2,t0)= Ф(t2,t1)* Ф(t1,t0) =>

=> Ф(t,t0)* Ф(t0,t) = Ф(t0,t)* Ф(t,t0)=E

Для вычисления обратной матрицы, нужно поменять местами аргументы: Ф^-1(t,t0)=Ф(t0,t)

Для стационарной системы:

Ф(t,t0)=+… (*)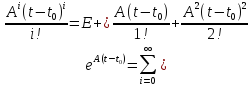

Проверим условия 1) и 2)

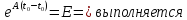
Рассмотрим простейший случай, когда матрица Aявляется диагональной

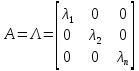
Ф(t,t0) =

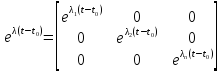
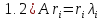, где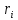- собственный вектор, соответствующий

Составим из векторов блочную матрицу R

R=,– вектор-столбец

AR=RΛ,Λ– диагональная матрица

А=RΛR^-1

Λ=R^-1AR, это справедливо для целых степенейk, т.е. А^k=RΛ^kR^-1,Λ^k=R^-1A^kR,

Подставляем А^k=RΛ^kR^-1в (*), производя преобразования получаем:

Алгоритм.

Отаскание собств. Знач. Матрицы А

Ищем собственные вектора , составляем матрицуRи находимR^-1

Находим Ф(t,t0)

Отыскание перех. матрицы с помощью обратного преобразования Лапласа

t0 = 0

,

Ф(t,0)==

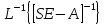
Еще один способ отыскания перех. Матрицы

x(t)=Ф(t,0)*x(0)

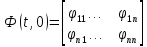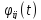,- описание перех. Процесса поi-ой координате вектора состояния, при задании единичного нач. условия наj-ую координату, при остальных равных 0.

Еще один способ – отыскание через ряды.

2.1) Решение линейной нестационарной системы в пространстве состояний.

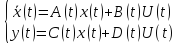
Найти решение x(t) начиная с некоторого момента времениt0 до ∞, представляющее собой траекторию вn- мерном пространстве, при задании входного воздействияU(t).

Решение ищем методом вариации постоянного, варьируя не скаляр, а векторную переменную.

Вектор состояния: ,k(t) –n– мерный вектор варьируемых параметров

Дифференцируем:

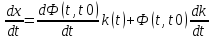
Подставляем x(t) в исходное уравнение:

=>=>

Вопрос существования 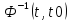закрывается теоремой:

На любом интервале времени, где A(t) интегрируема в смысле Римана, переходная матрица, удовлетворяющая свойству Ф(t,t0)=AФ(t,t0) является невырожденной.

Интегрируем

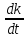
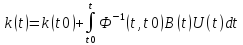, положимt=t0 (граничное условие)

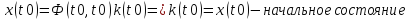
2.2)

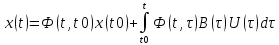
Примеры нестационарных систем: Система наведения, автоматическая система посадки самолета.

3.1) Решение линейной стационарной системы в пространстве состояний.

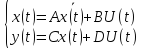
1)проверяем 1-е условие для переходной матрицы:

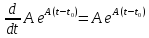
(да, условие выполняется)

2)граничное условие

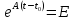
Воспользуемся аппаратом линейной алгебры. Рассмотрим простой случай, когда матрица А является диагональной.

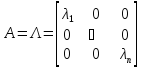
Приведем А к диагональному виду. ; -собственный вектор соответствующего собственного значения.

Из столбцов составим матрицу векторов:

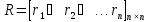
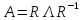
(преобразование подобия)

Справедливо для целых степеней -

3.2)

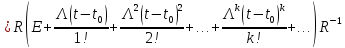
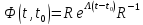
Алгоритм:

1)Отыскиваются собственные значения матрицы 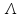(корни хар-го выражения)

2)Отыскиваем собственные вектора по выражению 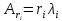. Строим матрицу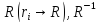

3)Подставляем в