10.Уравнение адиабаты идеального газа.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. δQ=dU+δA. δA=pdV и Cv=dU/dT pV=(m/M)RT=> => ; Сp/Сv=γж . Проинтегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, и потенцируя, придем к выражению или Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона. => - называется показателем адиабаты (или коэффициентом Пуассона).

11.Рaбота газа при адиабатическом процессе.

Cv=dU/dT . Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газ а 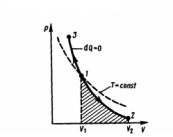Работа, которую совершает газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 2), меньше, чем при изотермическом, по причине, что при адиабатическом расширении осуществляется охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне такого же количества теплоты.

12.Теплоемкость идеального газа при политропическом процессе, ее связь с Ср и Сv.

Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. Теплоемкость при политропических процессах не зависит от температуры. Докажем это, рассмотрев 1 моль идеального газа.Cn=const(T).

13.Уравнение Ван-дер-Ваальса.

Ван-дер-Ваальса уравнение, одно из первых уравнений состояния реального газа, предложенное голландским физиком Я. Д. Ван-дер-Ваальсом. р — давление газа; Т — его температура; - объём одного моля вещества; R — универсальная газовая постоянная; а и b — константы, учитывающие отклонение свойств реального газа от свойств идеального. Член имеющий размерность давления, учитывает притяжение между молекулами газа за счёт ван-дер-ваальсовых сил. Константа b является поправкой на собственный объём молекул газа и учитывает отталкивание молекул на близких расстояниях. Константы а и b обычно определяются из экспериментальных данных. Ван-дер-Ваальса уравнение является приближённым и количественно описывает свойства реальных газов лишь в области высоких температур и низких давлений. Однако качественно оно позволяет описывать поведение газа при высоких давлениях, конденсацию газа в жидкость и критическое состояние(предельное состояние равновесия двухфазных систем, в котором обе сосуществующие фазы становятся тождественными по своим свойствам). 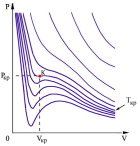-изотермы Ван-дер-Ваальса. При повышении температуры волнообразный участок уменьшается и превращается в точку (точка К). Эта точка называется критической.

14.Изотермы Ван-дер-Ваальса.

Ван-дер-Ваальса уравнение, одно из первых уравнений состояния реального газа, предложенное голландским физиком Я. Д. Ван-дер-Ваальсом. . -изотермы Ван-дер-Ваальса. На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма V при одинаковых значениях параметров p и T. Это соответствует существованию трёх действительных корней уравнения. При повышении температуры волнообразный участок уменьшается и превращается в точку (точка К ). Эта точка называется критической, а значения , и в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения Ван-дер-Ваальса.. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями . Для нахождения критических параметров подставим их значения в уравнение . Поскольку в критической точке все три корня совпадают и равны Vк уравнение приводится к виду: или , тогда => .Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами , и , величина которых зависит от свойств газа.