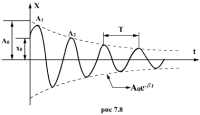
6.Затухающие колебания.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Все реальные колебательные системы являются диссипативными. при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления. где r - коэффициент сопротивления, v - скорость движения. или . Обозначим .β - коэффициент затухания. . , где U - некоторая функция от t. , введм , тогда . Тогд . -собственная циклич частота. -условный период затух колеб. Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания. . Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации. Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

7.Вынужденные колебания. Резонанс.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. , где . Решим уравнение без учета силы сопротивления: Причина такого возрастания амплитуды понятна: вынуждающая сила «во время» подталкивает шарик, при полном совпадении частот установившейся режим отсутствует – амплитуда возрастает до бесконечности.

8.Добротность колебательной системы.

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, называется декрементом затухания, a(t)/a(t+T)=a₀e^-t/a₀e^-(t+T)=e^T, а его логарифм – логарифмическим декрементом затухания : =ln(a(t)/a(t+T))=T=T/=1/N_e, где  – коэффициент затухания,  - время релаксации – время за которое ампл. уменьш. в е раз, N_e – число колеб. которое успевает сделать тело за время релакс. Величина Q=/=N_e называется добротностью колеб. сис-мы. Добротность пропорциональна числу колебаний N_e, совершаемых системой за то время , за которое ампл. колебаний уменьшается в е раз.

9.Различные формы записи уравнения состояния идеального газа.

Идеальный газ - теоретическая модель газа, в которой пренебрегается взаимодействие частиц газа, расстояние между молекулами много больше размеров молекул. Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. p = nkT . Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R = 8,31 Дж/моль·К. - уравнение состояния идеального газа. Изотермический - . Изохорный - или p0 – давление газа при T = T0 = 273,15 К .Коэффициент α, равный (1/273,15) К–1, называют температурным коэффициентом давления. Изобарный - или . Адиабатный процесс - это процесс, протекающий без теплообмена с окружающей средой. dA = -dU. пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок совершать работу F — сила, с которой газ действует на поршень. . Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. . -показатель политропы. const ; const;