38.Вязкость газов. Газокинетический вывод выражения для коэффициента вязкости.

Вязкость газов (явление внутреннего трения) — это появление сил трения между слоями газа некоторой толщины Dz, движущимися друг относительно друга параллельно и с разными по величине скоростями V₁ и V₂. . Взаимодействие двух слоев газа рассматривается как процесс, в ходе которого от одного слоя к другому передается импульс. Пусть в какой-то момент слои обладают импульсами K₁,K₂. Эти импульсы изменяются т.к. вследствие теплового движения происходит непрерывный переход мол. из одного слоя в другой. Число мол., переходящих через площадку S за сек. опред. выражением: N=(1/6)n<V>S (1). Через площадку S, лежащую на границе раздела слоев, переносится в ед. времени в направлении от первого слоя ко второму импульс: K=N(mV₁-mV₂), подставим (1): K=(1/6)n<V>Sm(u₁-u₂) (2). Скорость при переходе через границу раздела меняется по закону V=V(z). В среднем последнее соударение происходит на расстоянии, равном длине своб. пробега l. Поэтому молекулам, летящим в напр. оси z, припишем знач. скор. V₁=V(z-l), а мол. летящим в противоп. напр. V₂=V(z+l), подставим эти знач. в (2): K=(1/6)n<V>Sm[u(z-l)-u(z+l)]=-(1/6)n<V>Sm(dV/dz)2l, nm=r - плотность газа Þ K=-((1/3)<V>lr)(dV/dz)S, сравнив с формулой K=-h(dV/dz)S – импульс передаваемый за секунду от слоя к слою через поверхность S, получим выраж. для коэф. вязкости: h=(1/3)<V>lr.

39. Работа, совершаемая идеальным газом при политропическом процессе. Частные случаи.

Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. . -показатель политропы. const ; const; . ; ; ; ; для : ; ; ; ; для адиабатического и . Для изотермического . При изобарическом .Тот же результат, если n=0. При изохорическом A=0.

40.Диффузия газов. Газокинетический вывод выражения для коэффициента диффузии.

Диффузией  называется самостоятельное перемешивание молекул, обусловленное их тепловым движением. Диффузия имеет место как в газах и жидкостях, так и в твердых телах. В газах диффузия протекает с наиб. скоростью вследствие большой подвижности молекул газа. Скорость диффузии во всех агрегатных сост. в-ва сильно зависит от темпер. Получ. ур-я диффузии: будем считать, что молекулы обоих компонентов мало отлич. 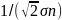по массе (m₁»m₂»m) и имеют практически одинаковые эффективные сечения s₁»s₂»s Þ <V₁>=<V₂>=<V>, <λ>= , где n₁+n₂=n. Допустим, что измен-е концентр. первого компонента вдоль z опис. ф-ей n₁=n₁(z). Обозн. число мол. первого компонента, пролет. за сек. через площ. S в напр. оси z, - через N’₁ и N”₁ в противоположных напр. Разность этих чисел даст поток молекулы первой компоненты N₁ через S: N₁=N’₁-N”₁ (1). Пусть мол. движутся вдоль взаимно перпендик. напр., совпад. с осями x, y, z (x,y||S). В этом случае число мол., пролет. за сек. в одном из напр. через единичн. площадку = (1/6)n<V> Þ N’₁ и N”₁ представимы в виде: N’₁=(1/6)n’₁<V>S, N”1=(1/6)n”₁<V>S (2), где n’₁, n”₁ – эффект. концентр. мол. первого компон. слева и справа от S, соответственно. В среднем последнее соударение происходит на расстоянии от S, равном средн. длине своб. пробега l. Поэтому вместо n’₁ разумно взять значение n₁(z-l), а вместо n”₁ – значение n₁(z+l). Тогда с учетом (1) и (2): N₁=(1/6)<V>S[n₁(z-l)-n₁(z+l)] (3). Т.к. l очень мала то: n₁(z-l)-n₁(z+l)=-(dn₁/dz)2l (4), подставим (4) в (3): N₁=-((1/3)<V>l)(dn₁/dz)S (5). Сравнив (5) с выражением для потока молекул i-го вида, N_i=-D(dn_i/dz)S, где D – коэф. диффузии, получим выраж. для коэф. диффузии: D=(1/3)<V>l. Вывод приведший нас к ф-ле (5), в равной мере применим к обоим компон. смеси. Þ D имеет для обоих компон. одинак. значен.