Дифракция рентгеновских лучей.

Большой интерес представляет дифракция на пространственных периодических структурах. Например, кристаллы, где можно наблюдать дифракцию рентгеновских волн, у которых λ соизмерима с межатомным расстоянием.

Впервые такой опыт поставлен по предложению Лауэ в 1912г. Причем оказалось, что за кристаллом на фотопластинке получилось центральное неотклонённое пятно и ряд закономерно расположенных пятен, распределенных в плоскости перпендикулярно от неотклоненного пучка рентгеновских лучей. Таким образом, случай дифракции на 3-х мерной решетке. Здесь открывается возможность определения λ ренгентовских лучей, если известна структура решетки кристалла, кроме того наблюдая дифракцию лучей с известной λ возможно найти структуру кристалла(рентгеноструктурный анализ). Но всё это представляет сложную стереометрическую задачу.

Ограничимся простейшим видом дифракции в отраженных лучах, рассчитанным Вульфом и Брэггом в 1913 г. Пусть расстояние между атомными слоями есть d. Падающие рентгеновские лучи рассеиваются на нескольких атомных плоскостях в различных направлениях. При интерференции рассеянных волн можно найти направления, где интенсивность будет наибольшей. Для этого надо, чтобы разность хода между лучами, отраженными от соседних атомных плоскостей = целому числу λ, т.е. где угол скольжения, дополняющей угол падения до .

Дифракция на ультразвуковых стоячих волнах.

Пространственную решетку, на которой можно наблюдать дифракцию видимых световых волн можно осуществить на ультразвуковых волнах. Например, в пластинке кварца или турмалина можно возбудить колебания Гц.

Поместив такую пластинку в жидкость (ксилол) получим ультраакустические волны в жидкости. Упругая волна в жидкости - это волна сжатая и разрежения, т.е. и различного показателя преломления. Поэтому для света получается фазовая решетка. Если заставить ультраакустическую волну отражаться от дна сосуда, то образуется стоячая ультраакустическая волна, которая представляет собой периодическую структуру переменной плотности с периодом = длине ультраакустической волны.

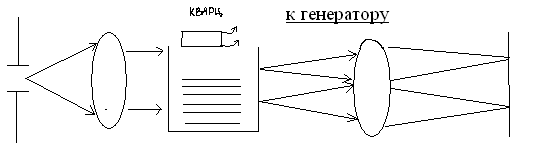
Например, в ксилоле скорость акустической волны 1000 и при из т.е. получается фазовая решетка периодом 10 мкм.

Если пустить ультраакустические волны по 3-м направлением, то получим пространственную решетку.

В таких решетках показатель преломления меняется еще и с периодом волны, т.е. раз в секунду. Это приводит к модуляции интенсивности дифрагировавшего света. Т.е если на ультраакустическую волну попадает свет с , то дифрагировавший свет будет иметь частоту , где N частота ультраакустической волны ~ .

Излучение дифракции света на ультраакустических волнах - важный метод исследования законов распространения этих волн в веществе.

Понятие о голографии – метод восстановления изображений без линз предложил и осуществил в 1948 году английский физик (венгр) Денис Габор.

Фиксируется полная информация о распределения амплитуды и фаз, волновых полей в отличие от фотографического метода, где фиксируется только распределение в пространстве интенсивности! Но именно фазы волн содержат в себе информацию о взаимном расположении частей источника света, о его удалении от приемника и т.д.

На голограмме регистрируется не само изображение предмета, а структура световой волны отраженной предметом.

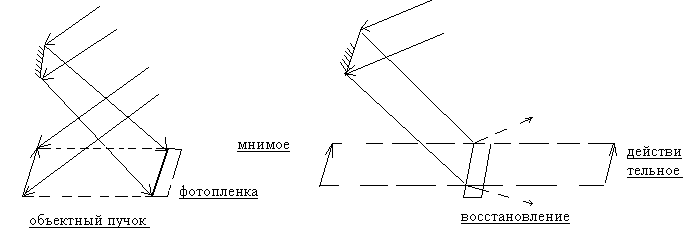
В 1962 году Ю.Н.Денисюк предложил метод регистрации голограмм в толстых Эмульсиях, толще, чем расстояние между полосами интерференции регистрируемого поля. Это позволяет получать объемную дифракционную решетку, при освещении которой можно восстановить даже спектр излучения. Это позволяет при считывании изображения использовать обычный свет.

Геометрическая оптика.

Геометрическая оптика как предельный случай волновой оптики.

Наблюдения показывают, что в свободном пространстве свет от точечного источника Р в точку А распространяется по прямой линии.

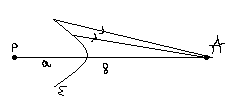
С точки зрения волновой оптики это можно объяснить:

Согласно принципу Гюгенса-Френеля амплитуда электромагнитного поля в точке А равна сумме амплитуд волн от вторичных сферических источников расположенных на вспомогательной поверхности Е, разбитой на зоны Френеля. Из диаграммы Френеля следует, что результирующая амплитуда в А в два раза меньше амплитуды поля создаваемого лишь первой зоной Френеля с радиусом . Таким образом, поля в А в основном определяется первой зоной. Так как выбор вспомогательной поверхности произволен, то можно представить себе на пути от Р к А множества таких поверхностей в каждой из которых определена своя первая зона Френеля.

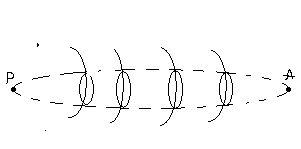
Мысленно соединим центры первых зон линией, а края отдельных зон соединим поверхностью. Форма такой поверхности похожа на сильно вытянутый эллипсоид с осью РА. Приняв а+b=с=соnst получим и при будет max.

Ясно, что внутри объема, ограниченного эллипсоидом (объем Френеля) в основном и распространяется свет. Радиусы поперечных сечений объема Френеля ~ и предельном случае λ→0 объем Френеля стягивается в линию, которую и называют лугом света. С физической точки зрения луч света- это жгут с поперечным размером равным размеру первой зоны Френеля. В пределах этой области поля световой волны, амплитуда которой равна амплитуде поля в пределах первой зоны Френеля, а фаза равна фазе поля в этой же области. Ясно, что при этом реальные изменения амплитуды и фазы поля в направлении перпендикулярно направлению распространения света очень малы const. Таким образом, амплитуда поля распространяющегося вдоль луча может быть выражена . Величину Ф(xyz) называют эйконал(от греческого - изображение).

Из волнового уравнения при λ→0 можно получить уравнение для определения и Ф. Из этих уравнений следует, что лучи распространяются по нормам к поверхности равного эйконала или равной фазы, называемых волновыми поверхностями. Для изохронных сред форма волновой поверхности совпадает с фронтами волны.