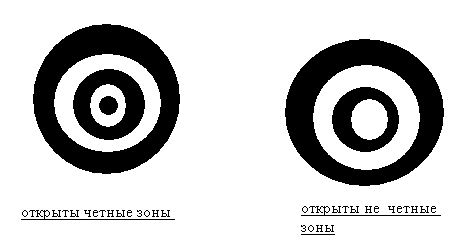
Зонная пластинка.

Очевидно, что если создать экран, перекрывающий излучений от всех честных или нечетных зон Френеля, он обеспечит значительное усиление интенсивность в точке наблюдения. Экран, функция пропускания которого обеспечивает перекрытия всех честных или нечестных зон Френеля, называется зоной пластинкой Френеля.

Если пластинку поставить на пути волны, то в точке В

и освещенность возрастает по сравнению со случаем свободного распространения света.

Векторная диаграмма содержит только ε витков спирали.

так как при изменении точки наблюдения условия оптимальной освещенности для данной зонной пластинки не выполняются, она создает значительную интенсивность света лишь в окрестности точки В для которой рассчитана. Поэтому зонная пластинка подобна собирающей линзе. Можно достичь еще большей яркости, если не зачернять зоны, а заставить их изменять фазу света на π (фазовая зонная пластинка).

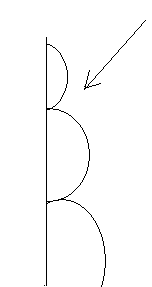
Простейшее дифракционные проблемы.

Будем пользоваться гипотезой положенной Френели в основу его рассуждений, пологая, что часть фронта волны прикрытия экраном не действует совсем, а неприкрытые участки действуют так, как если бы экрана порядка λ . Но при достаточно больших отверстиях влияния этой краевой зоны незначительно,

а) дифракция на кругом отверстии

Разбивка на зоны Френеля покажет, что в зависимость от размера отверстия в нем уложится большее или меньшее число зон. Если открыто нечетное число зон, то действия в точке В больше чем в отсутствие экрана. Для точек плоскости АВ вследствие симметрии всего расположения вокруг линии АВ распределение света должно симметрично, т.е. области одинаковой освещенности должны располагаться кольцеобразно около точки В.

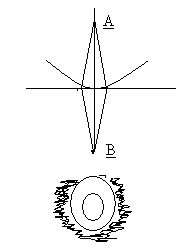
Если отверстие открывает нечетное число зон, то в центре светлое пятно. Если четное, то в центре экрана темнота.

б) Дифракция на круглом экране

Если размер экрана мал то действие 1-ой открытой зоны почти не отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в В будет ≈ такой же как и в отсутствии экрана. Вследствие симметрии относительно АВ светлая точка в В окружена кольцевыми зонами тени и света (вне границ геометрической тени).

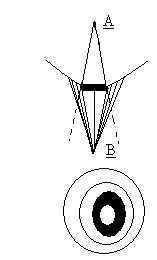
в) Дифракция на краю полубесконечного экрана.

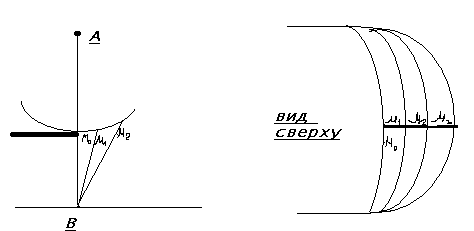
Решаем задачу путем разбиения поверхности волны на зоны так, что , отличаются на и затем из A проведем плоскости параллельные ребру экрана через

Площади таких лупок относятся как 1:0,41:0,32:0,27:0,22…..

Векторная диаграмма для точки В на линии перпендикулярна краю экрана.

По мере того как точка В будет смещаться параллельно экрану в сторону освещенной части пространства. Будет открываться новые зоны. Если удалиться от края экрана так, что его действие можно не учитывать, то векторная диаграмма будет спиралью Корню.

Дифракция Фраунгофера.

До сих пор мы рассматривали дифракцию сферическую (или плоских) волн и изучали дифракционную картину на конечном расстоянии от препятствия (дифракция Френеля). При больших удалениях от экранам с неоднородного (например, со щелью), на поверхности щели уложиться лишь часть первой зоны Френеля. Тип дифракции, при котором рассматривается дифракционная картина образованная параллельными лучами называется дифракцией Фраунгофера. Например

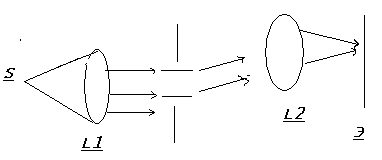
Такой тип дифракции можно рассматривать математически до конца.

Помещая между линзами разные экраны, мы меняем характер дифракционной картины, являющейся изображение источника.