Дифракция света.

Наблюдения за прохождением света через непрозрачный экран с отверстием выявляет следующее: Если размер отверстия >> λ волны, то свет распространяется за экраном по прямой и дает изображение отверстия на втором экране. При уменьшении отверстия изображение отверстие так же будет уменьшаться, однако, до определенного предела.

Как только размер отверстие становиться сравнимым с λ света, наблюдается огибание светом препятствия - размер изображения отверстия начинает увеличиваться при его сужении.

Явление отклонение света от закона прямолинейного распространение при прохождении через экраны называется дифракцией.

Отклонение света от прямолинейного направления распространения происходит и в тех случаях, когда на его пути находится небольшая преграда или среда, показатель преломления который завит от координат. Таким образом, дифракция наблюдается всегда, когда свет проходит через среду или экран с оптическими неоднородностями.

С точки зрения эл/м теории явлении дифракции объясняется тем, что распространение света подчиняется волновому уравнению, при существовании каких-либо препятствий в пространстве однородность условий распространения эл/м волн нарушается, следствием его и является дифракцией.

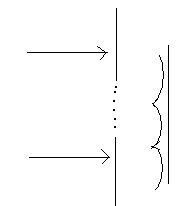
Впервые дифракцию с волновой точки зрения рассмотрел голландский физик Х.Гюгенс. Сформулированный им принцип: Пусть возмущения (волна) распространяется в некотором направлении и известно положение волнового фронта в некоторый момент t, а также скорость распространения волны c.

Примем каждую точку фронта за источник вторичных волн. Посмотрим элементарные волны радиуса и проведем огибающею их поверхностей. Она и определит положение фронта в момент

Этот принцип нечего не говорит о распространении амплитуд по фронту волну.

Французский физик Френель (1788-1827) дополнил принцип Гюйгенса, предложив, учитывать интерференцию вторичных волн и разработал, для этого метод расчета. Френель не только рассчитывал дифракционные задачи, но объяснить прямолинейность распространения света в свободном пространстве, что было триумфом нового метода и способствовало всеобщему признанию волновой теории света.

Последующие исследования Максвелла, Киргофа, Грина позволили обосновать представления Гюйгенса – Френеля и показали, что по существу он является одним из методов решения волнового уравнения с заданными граничными условиями.

Зоны Френеля.

Рассмотрим действия световой волны, испущенной из А в какой-нибудь точке наблюдения В. Согласно принципу Гюйгенса – Френеля заменим действия источника А действием воображаемых источников, расположенных на вспомогательной поверхности S(поверхность фронта волны идущей из А)

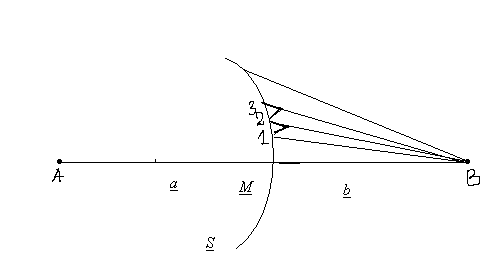
Вычисления результата интерференции вторичных волн очень упрощается, если для вычисления действия в точке В разбить поверхность S на зоны такого размера , чтобы расстояние от краев зоны отличались на .

Для первой зоны:

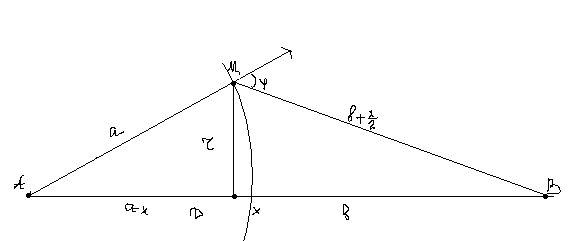
Или 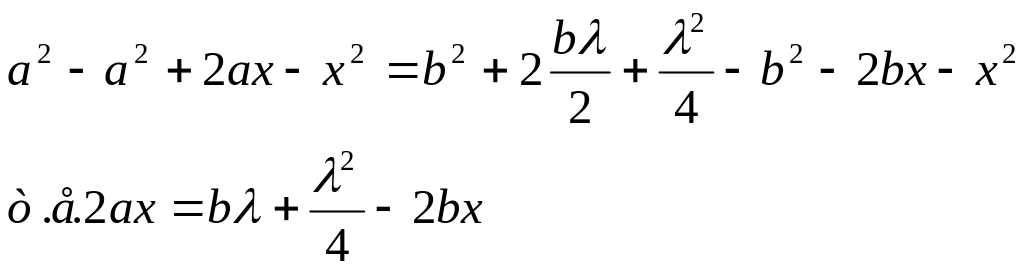; так как λ>> а;в то пренебрежение числом с :

или

Площадь сегмента 1- ой зоны , так как r мало или:

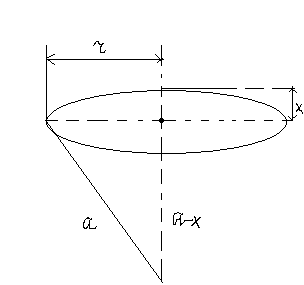
Площадь 2-ой зоны:

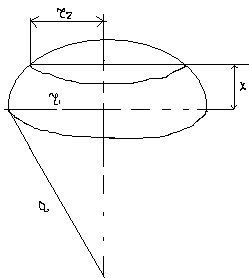
Следующие зоны тоже имеют такую же площадь. Таким образом, площадь(поверхность)сферической волны разбирается на одинаковые по площади зоны в В есть , соседний и т.д.

так как угол φ разный. Благодаря выбранному способу разбиения действия соседних зон ослабляют друг друга, так как (противофазе).

Окончательное значение амплитуды в В будет

в скобках выражение>0. поэтому таким образом, действия всей волны в В сводиться к действию её малого участка (<центральной зоны с площадью ).

Так как мм, то даже для а и b ~1мм площадь действующей части волны . Таким образом, распространение света от А и В происходит так, как если бы световой поток шел внутри очень узкого канала (прямолинейно).

Но это не означает , что если на линии АВ поместить небольшой экран, то до В свет не дойдет. Например, если закрыть 1-ую зону, то выпадет 1- ый член ряда и окажется и т.д., , где m номер первой открытой у экрана зоны.

Если размер отверстия в непрозрачном круглом экране такой, что открытым остается четное число зон, то S→0 и в В будет «темнота». Изменение диаметра к периодическому усилению и ослаблению света при проходе от четного к несчетному числу открытых зон.

Более того, если перемещать точку наблюдения вдоль прямой АВ начав с расстояния на котором, например отверстие оставляют открытой одну зону и приближаться к экрану, то число открытых зон будет расти, а потому снова должны наблюдаться по переменные переходы от света к темноте.

Так как наибольшее значение суммы ряда получается если открыта одна зона, то это можно истолковать как получение изображения точечного источника (камер-обскуры).

Полученные результаты можно сделать наглядными при помощи векторной диаграммы. Разобьем первую зону на большое число равновеликих кольцевых зон. Пусть колебания создаваемые частью зоны прилегающей к оси ОА изображаются вектором . Каждая следующая часть зоны создает колебания, изображаемые таким же по модулю вектором, повернутым на малый угол, учитывающий сдвиг фазы. Так как фазы колебания от центра и края 1-ой зоны сдвинуты на , получим половину правильного многоугольника (полуокружность) . Действия 2-ой зоны тоже полуокружность меньшего радиуса, так как амплитуда колебания уменьшается. Продолжая построение, получим спираль. Тогда амплитуда колебания в точке наблюдения изобразится отрезком КТ. Если же на пути световой волны экран с отверстием, на котором укладывается, например, одна или три зоны, то амплитуда колебаний будет или . Напротив, при четном числе зон амплитуды и оказываются малыми.