18. Шифры совершенные по Шенону.

Первая Условная вероятность и вторая условная вероятность 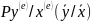где .

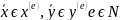Имеет смысл рассматривать x и y одинаковой длины. пусть , , 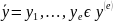для шифра с ограниченным ключом условная вероятность появления шифротекста (1) . выполняется следующее условие

при 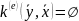. , при этом распределение вероятностей определяется через оприорное распределение на множестве ключей шифра Pk. Условную вероятность можно вычислить по стандартной формуле 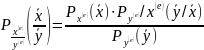.(2)

Шифр называется совершенным по Шенону если для любых и для любого натурального числа l, выполняется неравенство .Часто бывает удобно пользоваться альтернативным вариантом определения шифра . Покажем что совершенным может быть шифр с неограниченным ключом, и критерием совершенности такого шифра является свойство совершенности его опорных шифров.

Шифр с ограниченным ключом .

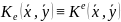Шифр с неограниченным ключом .

Если шифр является совершенным то для любых , и любого натурального числа e выполняется следующее неравенство

Доказательство: 1.от противного: пусть тогда мы бы имели согласно первому следующее равенство 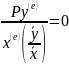. А согласно второму

А из третьего следует .

Шифр с ограниченным ключом не является совершеннм.

Если взять и зафиксировать символ , то согласно второму найдется ключ , поэтому для совершенного шифра мощность ключевого потока должна быть , где K это константа. В соответствии с этим получаем что .С ростом l величина Y(l) неограниченно растет.

Совершенными могут быть лишь только шифры с неограниченным ключом.

Шифр с неограниченным ключом является совершенным, тогда и только тогда, когда его l- опорный шифр является совершенным при любом l принадлежащим N. Такой подход позволяет нам при изучении свойств шифром, рассматривать лишь их опорные шифры. Под шифром будем понимать совокупность ( , , , , состоящей из случайных величин, заданных на конечных множествах x-открытых текстов и y-шифрованных текстов. В соответствии с априорным распределением вероятностей

. При этом |x|>1, |1|>1, |k|>1, а также правил зашифрования таких что . Полагаем что случайные величины и 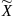независимы.

Вероятность появления 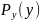вычисляется обычно по формуле . Из общих соображение следует следующее равенство .

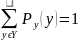Если шифр совершенен то справедливы следующие неравенства |X|≤|Y|≤|K|, первое неравенство очевидно, если шифр совершенен то согласно доказательству утверждения 2, | |≥1 по этому для любого x X. { }=Y и по этому в большинстве случаев применяемые на практике шифр обладают следующим…

Шенону удалось описать эндоморфные шифры с минимально возможным числом ключей. Это число не меньше чем |Y|.

19.Теоретическая стойкость шифра с позиции теории информации.

Сложность вскрытия поточного шифра простой замены зависит от характера открытого текста. Все достаточно просто, если шифрованию подвергается литер-ный текст. Однако задача усложняется, если перед шифрованием тот же текст сжать при помощи архиватора. И наложенный критерий на отрр текст становится аморфным для 2го случая. Это объясняется избыточностью текста как инреграль. хар-ки данного языка. Речь идет о том, что в норматив текстах каждая буква или знак препинания передает небольшое кол-во инф-,и от некот. из них можно отказаться без ущерба для передаваемой инф-и.

Избыточность текса дает возможность сжимать его при архивации. В связи с этим возникает вопрос об избыточности текста и ср кол-вом инф-и, передаваемой отдельной буквой. Рассмотрим некот. модель отк. текста. В основу возьмем к-граммную модель. В этом случае имеем дело со случайной величиной, распределение кот опред-ся ЧХ языка. В этом случае откр текст можно представить как последовательность испытаний случайной величины:

при k=1. Р(а), р(в), …, р(я) – вероят-ти появления букв в открытом тексте. Кол-во инф-и, извлекаемое из эксперимента по угадыванию исх. случайной величины:

,

Если для любого i, то .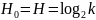

Причем Н=0 только в том случае, когда .

Для биграммной модели текста, учитывающего зависимость появления знака текста от предыдущего знака кол-во инф-и на знак отк. текст опр-ся след ф-лой:

n – мощность алфавита

- вероятность появления j символа вслед за i символом. - вероятность появления I символа.

Единицу измерения энтропии дает теорема кодирования, кот утверждает, что любой исход случайной величины ξ можно закодировать символами 0 или 1. Так, что получ. длина кодового слова будет близка сверху к Н. На основании этого энтропия измеряется в битах.

Под кодированием случайной величины ξ понимается ф-я f отображения, кот. отображает случайную величину ξ в один из эл-ов множ-ва 0, 1.

Если требуется однозначность кодирования, то отображение должно быть инъективным. Отображение f естественно продолжается до кодирования строк исходов:

( ):f( )=f( , f( ,…, f( .

При этом слова приписываются друг за другом. Мерой эффективности кодирования яв-ся средняя длина кодового слова, кот опред-ся след образом:

L(f)=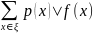

Кодирование которое минимизирует l(f) наз-ся оптимальным. Оптимальные коды: Хэмминга, Фано, Хаффмана.

Величину среднего кол-ва инф-и приходящейся на одну букву откр. текста языка Λ обозначают 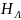и называют энтропией одного знака. Энтропию языка вычисляют последовательными приближениями, определяемыми ростом r в r-граммной модели откр. текста.

Первым приближением открытого текста яв-ся энтропия случайного текста. Вторым приближением служит позначной модели, в кот. совпадает с вероятностью появления буквы 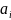в открытом тексте.

В качестве следующего более точного приближения применяется энтропия вероятностного распределения биграмм деленная на 2. В общем случае, берется энтропия вероятностной схемы на r- граммах деленная на r.

Исследования показывает, что для естественных языков сремится к конечному пределу r.

А формула 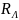= 1 - – определяет избыточность языка .

Термин «избыточность языка» возникает в связи с тем, что макс. инф-я, кот. могла нести каждая буква сообщения равна .

.

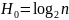Средняя энтропия буквы в открытом тексте значительно меньше, и след-но, каждая буква несет больше инф-и, чем .

Величина характеризует неиспользованные возможности букв в передаче информации, а соотношение:

– «неинформативная» доля букв.

В пересчете на весь текст это сообщение характеризует долю лишних букв. Исключение этих букв из текста не приведет к потере инф-и, потому что она будет восстановлена исходя из знаний остальных букв.

Колмогоров предложи комбинированный подход к определению . Суть его подхода состоит в том, что кол-во инф-и, кот приходится на одну букву текста определяется тем условием, что число открытых текстов длины l удовлетворяющих закономерностям языка при достаточно больших l равно не 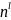= . Как это было бы, если бы мы имели право брать любые наборы букв из l букв, и будет равна: М(l)= .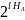

По сути это и есть асимптоматика осмысленных текстов длины l для данного языка Λ. Исходя из этого можно определить:

Величину М(l) можно оценить с помощью подсчета возможных продолжений литературного текста. Такая работа была проведена с использованием русского языка.

Попытаемся использовать энтропия и избыточность языка для анализа стойкости шифра.

Попытки определения ключа шифра по данной криптограмме путем ее расшифрования на всевозможных ключах могут привести к тому, что критерий на открытый текст примет несколько претендентов на открытый текст.

Для нахождения оценки числа ложных ключей для шифра требуется условная энтропия: 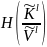ξ, n – случайные величины, заданные вероятностными распределениями. Для них можно вычислить совместное распределение и условное: р(ξ,η), р(ξ/η), р(η/ξ).

Тогда условная энтропия 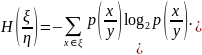Усредненная по величина условной энтропии наз-ся условной энтропией ξ и η и будет равна:

Эта величина измеряет среднее количество информации о ξ, обнаруживаемую с помощью η. Из курса теории информации известно, что имеет место след нер-во: , причем равенство будет только тогда, когда ξ и η – независимые величины. Шеннон назвал условную энтропию ненадежностью шифра по ключу. Она измеряет среднее количество информации о ключе, который дает текст длины l.

Лучшей при заданном распределении P( ) яв-ся ситуация, когда случайная энтропия принимает максимальное значение: . Именно в этом случае шифр можно считать совершенно стойким.

Связь между энтропиями компонент шифра дает доказанная Шенноном формула для ненадежности шифра по ключу: )+ )- )

Эта формула позволяет получить оценку среднего числа ключей шифра с ограниченным ключом. Рассмотрим эндоморфные шифры с ограниченным ключом и мн-во открытых текстов с известной избыточностью. Зафиксируем l b , отвечающих данной криптограмме: . В таком случае естественно определить :

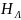= H( )/l.

Введем обозначения: .

Число ложных ключей отвечающих данной криптограмме будет равно:

Так как лишь один из допустимых ключей является истинным, определяется среднее число ложных ключей относительно всех возможных шифротекстов длины l следующей формулой: ,

Теорема: Для эндоморфного шифра с ограниченным ключом выполняется условие:

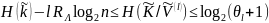, где n- число шифровеличин, – избыточность языка пересчитанная на шифровеличину.

Следствие: Для эндоморфного шифра с ограниченным ключом число ложных ключей удовлетворяет следующему неравенству:

В частном случае, когда все ключи шифра равновероятные, число ложных ключей удовлетворяет следующему неравенству: -1

Минимальное l удовлетворяющее этому неравенству называется расстоянием единственности шифра.

эта величина является приближением минимальной длины шифротекста, По которой однозначно можно восстановить ключ. существенно зависит от избыточности текста.