
- •Основные этапы становления криптографии как науки
- •Простейшие шифры, их свойства. Шифры замены и перестановки.
- •3. Открытые сообщения и их характеристики.
- •4. Частотные характеристики открытых сообщений.
- •5. Критерии на открытые сообщения.
- •6. Основные понятия криптографии
- •7. Криптосистема, ключевая система шифра, основные требования к криптосистемам.
- •8. Шифр перестановки. Разновидности.
- •9. Криптоанализ шифров перестановки.
- •10. Шифр замены, одноалфавитные и многоалфавитные замены.
- •11. Вопросы криптоанализа простейших шифров замены.
- •12. Поточные шифры замены.
- •13. Табличное и модульное гаммирование. Случайные и псевдослучайные гаммы.
- •14. Криптограммы, полученные при повторном использовании ключа.
- •Вопрос 15. Математическая модель шифра. Опорный шифр.
- •Вопрос 16. Шифр с неограниченным ключом
- •Вопрос 17. Модель шифра с ограниченным ключом.
- •18. Шифры совершенные по Шенону.
- •19.Теоретическая стойкость шифра с позиции теории информации.
- •20. Безусловно и вычислительно стойкие шифры. Избыточность языка и расстояние единственности.
- •21. Имитостойкость шифра. Имитация и подмена сообщений.
- •22. Характеристики имитостойкости. Методы обеспечения имитостойкости.
- •23. Совершенная имитостойкость.
- •24. Линейные регистры сдвига
- •25. Помехоустойчивость шифров. Характеристики помехоустойчивых шифров.
- •26. Основные способы реализации криптографических алгоритмов и требования к ним.
- •27. Методы получения случайных и псевдослучайных последовательностей.
- •28. Методы анализа криптоалгоритмов. Понятие криптоатаки.
- •29. Методы анализа криптоалгоритмов. Перебор ключей
- •30. Методы анализа криптоалгоритмов. Метод встречи посередине.
- •31. Методы анализа криптоалгоритмов. Бесключевые методы.
- •32. Система шифрования с открытым ключом. Понятие односторонней функции с секретом.
- •33. Криптосистемы rsa.
- •34. Криптосистема Эль-Гамаля.
- •35. Проблема факторизации целых чисел и логарифмирование в конечных полях.
- •36. Американский стандарт шифрования des
- •37. Российский стандарт шифрования гост 28147-89
- •38. Шифр rc4
- •39. Шифр Rijndael. Математические основы работы.
- •40. Шифр Rijndael. Работа с байтами состояния.
- •41. Шифр Rijndael. Алгоритм выработки ключей.
- •43. Криптографические протоколы. Модели криптографических протоколов.
- •Классификация
- •44. Электронная цифровая подпись. Стандарты эцп.
- •45. Математические основы шифрсистем на эллиптических кривых.
- •46. Свойства множества точек эллиптической кривой.
- •47. Выбор параметров на эллиптической кривой. Шифр Эль-Гамаля на эллиптической кривой.
- •48.Эцп на базе эллиптической кривой.
- •49. Протоколы установления подлинности. Парольные системы разграничения доступа.Протокол рукопожатия.
- •50. Криптосистема на алгоритме а5
- •51. Протоколы сертификации ключей. Протоколы распределения ключей.
- •52. Протоколы выработки сеансовых ключей. Открытое распределение ключей Диффи-Хеллмана.
14. Криптограммы, полученные при повторном использовании ключа.
Предполагаем,
что алфавитАоткрытых
текстов, гаммы и шифротекстов представляет
собой множество чисел Zn
= {0,1,...,и-
1} . Пусть в распоряжении криптоаналитика
оказались две криптограммы, полученные
наложением одной и той же гаммы на два
разных открытых текста:
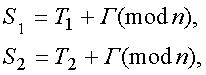
где
![]()
Рассмотрим
возможности криптоаналитика по
восстановлению исходных открытых
текстов. Прежде всего, можно найти
позначную разность
![]()
Пусть S = {si}i=1,2,… Тогда поставленная задача сводится к попытке подобрать пару открытых текстов, разность которых совпадает с известной последовательностью S. Будем в связи с этим говорить о разложении Sна два составляющих открытых текста. В случае, когда данные тексты являются нормативными текстами, например, на русском, английском или другом языке, для решения последней задачи используется ряд подходов. Интуитивно понятно, что при достаточной длине текстов маловероятна возможность множественного представления данной последовательности Sв виде разности Т1-Т2. Как правило, такое разложение бывает единственным. Здесь имеет место приблизительно такая же ситуация, как и при рассмотрении вопроса о расстоянии единственности.
Один из таких подходов (хорошо известных из истории криптографии) связан с использованием некоторого запаса слов или словоформ, часто встречающихся в открытых текстах. Это могут быть, например, стандарты переписки, частые k-граммы и т.п.
Предположим
сначала, что одно из вероятных слов
встретилось в начале первого сообщения:
![]()
В
таком случае можно вычислить начало
второго сообщения:
![]()
Если l> 4, легко определить, является ли начало Т2"читаемым" или нет. В первом случае нужно попытаться продлить начало Т2по смыслу. Во втором случае нужно сдвинуть начало вероятного слова в Т1и проделать то же самое.
Если
удалось развить Т2до
т
знаков
(т>l):
Т2
=
 ,
то можно вычислить и соответствующие
т-1
знаков
,
то можно вычислить и соответствующие
т-1
знаков
![]() и попытаться, в свою очередь, развить
по смыслу Т1.
и попытаться, в свою очередь, развить
по смыслу Т1.
Продолжая этот процесс далее, мы частично или полностью восстановим оба текста или убедимся в том, что опробуемого вероятного слова данные тексты не содержат. В последнем случае следует попытаться ту же процедуру проделать для следующего вероятного слова. Может оказаться так, что при опробовании некоторого слова удается восстановить лишь часть каждого из текстов, а дальнейшее развитие их по смыслу бесперспективно. В таком случае следует продолжить работу с другим вероятным словом.
Вопрос 15. Математическая модель шифра. Опорный шифр.
Под шифром понимается любой симметричный шифр, однозначной замены алфавитом которого служит множество шифр-величин. Это множество адаптировано к способу шифрования. Выбор той или иной простой замены осуществляется с помощью ключевого потока(распределителя), который представляет собой последовательность номеров простых замен. Ключевой поток может получаться случайным образом, на пример с помощью «рандолизатора» типа игровой рулетки. Такой шифр мы будем называть шифр с неограниченным ключом. Ключами шифра служат всевозможные ключевые потоки. Шифр с неограниченным ключом полностью определяется своим действием на множестве шифр-велечин и рандомезаторе, ключевой поток может также функционально зависеть от ключа шифра и вычисляться детерминировано(по некоторому алгоритму или программе). Число возможных ключевых потоков фиксированной длины, не превосходит числа ключей шифра. Такой шифр будет называться шифром с ограниченным ключом. На практике чаще всего используются шифры с ограниченным ключом. Ключевым потоком для таких ключей служит последовательность некоторого автономного автомата, множество состояния которого совпадает с множеством ключей шифра.
Пусть
Х и Y
кончное множество шифровелечин и
шифрообозначений, с которыми оперирует
некоторый шифр замены. |X|>1
|Y|>1
|Y|>=|X|
это означает что открытые и шифрованный
тексты представ в алфавите X
и Y,
процесс шифрования открытого текста
Заключается в замене каждой шифровелечины
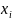 на некоторой шифрообозначение.
на некоторой шифрообозначение.
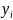 В соответствии и с одним из n>1
иньективных отображений
В соответствии и с одним из n>1
иньективных отображений
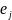 .
Индексированных числами j
принадлежит К.
.
Индексированных числами j
принадлежит К.
Будем
называть отображение
простыми заменами. Заметим что максимальное
число n
(простых замен составляющих шифр замены)
не превосходит числа размещений
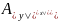 .
Пусть
.
Пусть
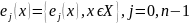 .
.
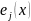 ->
X
->
X
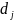 (
( )=x,
все x
)=x,
все x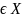
Известно
что Y=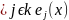
Определение №1. Опорным шифром шифрозамены назовем совокупность ∑=(X,Y,K,E,D) в которой X и Y- множество шифровелечин, K-множество ключей, Е-множество иньективных отображений и D- множество правил расшифрования.
K=(0,1,…,(n-1))
E=(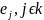 )
D={di,j
ϵ k}
)
D={di,j
ϵ k}
Определение
2. l-ой
степенью назовем совокупность объектов
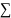 =(
=(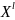 ,
,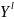 ,
,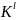 ,
, ,
,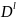 ),
l
ϵ N,
в которой
,
,
декартовы степени множеств X,Y,K
соответственно.
),
l
ϵ N,
в которой
,
,
декартовы степени множеств X,Y,K
соответственно.
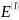 -
множество правил шифрования.
-
множество правил шифрования.
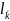 :
: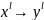 ,
,
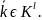 Таких
что для
Таких
что для
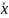 =
=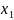 ,
…,
,
…,
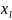 ϵ
и
ϵ
и
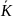 =
=
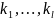 ϵ
ϵ
Правило
зашифрования
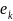 (
)=
(
)=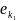 (
)
…
(
)
…
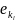 (
)
ϵ
,
(
)
ϵ
,
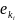 ϵ E,
i=1,l
ϵ E,
i=1,l
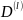 -множество
состоящее из отображений
-множество
состоящее из отображений
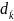 :
: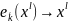 ,
,
 ,
таких что для
,
таких что для
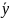 =
=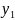 ,
…,
,
…,
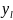 ϵ
(
ϵ
(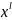 )
и
)
и
 =
=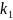 ,
…,
,
…,
 ϵ
ϵ
(
)=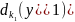 …
…
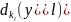 ϵ
,
ϵ
,
 ϵ D,
, i=1,l
ϵ D,
, i=1,l
При
l=1
l-опорный
шифр
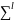 будет
равен ∑ (
будет
равен ∑ (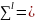 ∑)
∑)
Введя понятие степени опорного шифра мы определили действие шифра замены на последовательность шифро-велечин, т.е элементарных единиц открытого текста.
Ключевой
поток строится следующим образом:
последовательность
,…, ϵ K
номеров простых замен
ϵ K
номеров простых замен
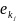 ,
используемых для зашифрования открытого
текста
,
используемых для зашифрования открытого
текста
 =
,
…,
ϵ X,
i=1,
l.
=
,
…,
ϵ X,
i=1,
l.
Имеются два принципиальных способа построения такой ключевой последовательности. Если нужно выбрать один из двух вариантов, достаточно подбросить монету. Аналогично можно поступить для случайного выбора одного из 2^m вариантов, достаточно подбросить монету m раз подряд. Заметим что исходы бросания образуют последовательность испытаний случайной велечины кси,которая будет принимать значения 0 и 1 с вероятностями p и q. 0 будет орел, 1 решка.
В
место монеты можно использовать любой
рандомизатор. Используя приведенную
аналогию, будем в первом случае строить
ключевой поток с помощью некоторого
рандомизатора, который выбирает тот
или иной ключевой поток длины l,
в соответствии с некоторым априорным
распределение вероятностей заданным
на множестве
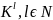 .
.
Этот
выбор производится в соответствии с
частотными характеристиками открытых
текстов. Характеристики для обычных
открытых текстов далеко не равномерное.
Пусть p(
)={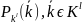 }
(3)
}
(3)
p(
)={ }
(4)
}
(4)
Это
априорно выбранные распределения
вероятностей. Обозначим через… случайные
велечины которые принадлежат значениям
из
,
в соответствии с распределениями в
законах (3)и(4). По определению эти случайные
величины полагаем независимыми.
Используем понятие l-опорного
шифра, в данном случае под ним будем
понимать пятёрку (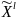 ,
,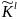 ,
,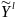 ,
,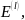
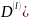 где
,
-случайные
величины,
-случайная
величина с множеством исходов
где
,
-случайные
величины,
-случайная
величина с множеством исходов
P(
)={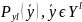 }
}
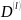 -правила
шифрования и расшифрования соответственно.
-правила
шифрования и расшифрования соответственно.
Распределение
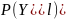 индуцируется распределением
индуцируется распределением
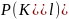 она зависит от
она зависит от
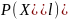 .
И её можно оценить
.
И её можно оценить
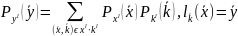
В
ряде случаев не всякое слово длины l
в алфавите x
может появится в открытом тексте.
Например для l=2
слово из «ъъ» вероятность появления
равна 0. А с точки зрения шифрования
совершенно безразлично, встретится
такая биграмма в тексте или нет. По этому
исключим из открытых текстов
исключим l-грамм
и будем рассматривать
>0.
Это условие мы используем при изучении
совершенных шифров. Запрещенных l-грамм
не слишком много, точнее что для всех
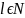 выполняется следующее неравенство
|
выполняется следующее неравенство
|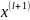 |>|
|>| |,
любой открытый текст можно удлинить
некоторой шифровелечиной до открытого
текста большей величины. При этом
полагаем что
|,
любой открытый текст можно удлинить
некоторой шифровелечиной до открытого
текста большей величины. При этом
полагаем что
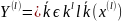 .
.
Определение
3. Пусть
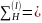 (
,
,
,
где совокупность случайных чисел
,
,
, множество правил шифрования и
расшифрования
для которых выполняется следующее
условие P{
(
,
,
,
где совокупность случайных чисел
,
,
, множество правил шифрования и
расшифрования
для которых выполняется следующее
условие P{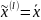 }>0,
P{
}>0,
P{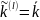 }>0,
все
}>0,
все
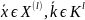 . Тогда шифром замены с неограниченным
ключом назовем семейство
. Тогда шифром замены с неограниченным
ключом назовем семейство
 =(
=(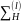 ,l
,l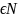 )
сумма всех шифров длинны l.
При этом совокупность
будем называть l-опорным
шифром.
)
сумма всех шифров длинны l.
При этом совокупность
будем называть l-опорным
шифром.
