35. Проблема факторизации целых чисел и логарифмирование в конечных полях.
Факторизацией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики
В зависимости от сложности алгоритмы факторизации можно разбить на две группы: экспоненциальные алгоритмы, субэкспоненциальные алгоритмы.
Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере.
Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA.
Логарифмирование в конечных полях иными словами Дискретное логарифмирование (DLOG) – задача обращения функции gx в некоторой конечной мультипликативной группе G.
Задача дискретного логарифмирования является одной из основных задач, на которых базируется криптография с открытым ключом. Идея, лежащая в основе подобных систем, опирается на высокую вычислительную сложность обращения некоторых числовых функций. В данном случае, операция дискретного логарифмирования является обратной к показательной функции. Последняя вычисляется достаточно просто, в то время как даже самые современные алгоритмы вычисления дискретного логарифма имеют очень высокую сложность, которая сравнима со сложностью наиболее быстрых алгоритмов разложения чисел на множители.
Другая возможность эффективного решения задачи вычисления дискретного логарифма связана с квантовыми вычислениями. Теоретически доказано, что, используя их, дискретный логарифм может быть вычислен за полиномиальное время[2]. В любом случае, если полиномиальный алгоритм вычисления дискретного логарифма будет реализован, это будет означать практическую непригодность криптосистем на его основе.
Классическими криптографическими схемами, базирующимися на сложности задачи дискретного логарифмирования, являются схема выработки общего ключа Диффи-Хеллмана, схема электронной подписи Эль-Гамаля, криптосистема Мэсси-Омуры для передачи сообщений.
36. Американский стандарт шифрования des
Был опубликован в 1977 году, национальным бюро стандартов США. Клод Шенон высказал такое мнение что в практических шифрах необходимо использовать 2 общих принципа: рассеивание и перемешивание.
Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифротекста. Это позволяет скрыть статистические характеристики в шифротексте.
Перемешивание предполагает использование таких шифрующих преобразований которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текста.
Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, т.е шифра который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.
В составных шифрах чаще всего используются простые перестановки и подстановки. В современном блочном шифровании блоки открытого текста и шифротекста представляют собой двоичные последовательности обычно длинной 64 бита. В принципе каждый блок может принимать 2 в 64 степени значений. По этому подстановки выполняются в очень большом алфавите содержащим 2 в 64 степени символов. И при многократном чередовании простых подстановок и перестановок управляемых достаточно длинным ключом, можно получить достаточно стойкий шифр с хорошим рассеиванием и перемешиванием.
Стандарт DES предназначен для защиты от несанкционированного доступа к важной но не секретной информации в государственный и коммерческих учреждений США. В 1980 стандарт был одобрен национальным институтом технологий.
Основные достоинства алгоритма DES:
1. Используется только один ключ длинной 56 бит.
2. зашифровав сообщение с помощью одного пакета программ, для расшифрования можно использовать любой другой пакет , одобренный DES.
3. относительная простота алгоритма обеспечивает высокую скорость обработки.
4. достаточно высокая стойкость алгоритма.
Первоначально этот метод был разработан фирмой IBM для своих целей и реализован в системе «люцифер». В ней использовался ключ длинной 128 бит который управлял состоянием блоков подстановки и перестановки. Алгоритм был очень сложен в практической реализации из-за относительно малой скорости шифрования, программная реализация 2 кбайта, аппаратная реализация 9кбайт.
Структура DES:
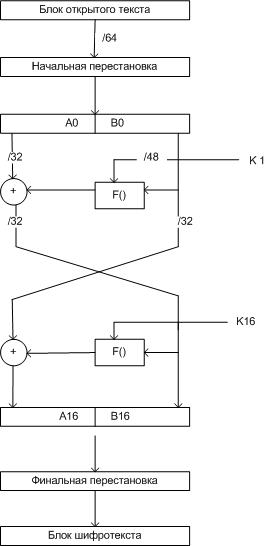
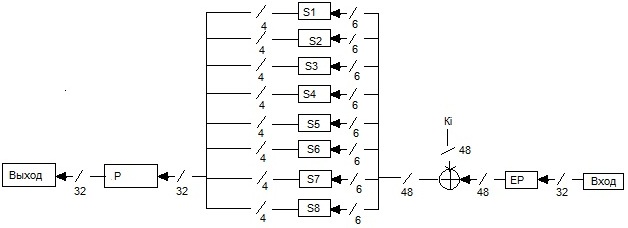
Функция раунда DES: рис
Расширение ключа DES
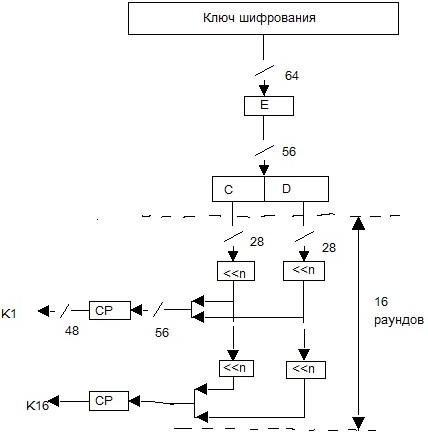
Биты входного блока Т (64 бит), переставляется в матрице,58 бит станов 1, 50 бит станов 2 и т.д
По окончанию шифрования получается матрицы обратной перестановки.
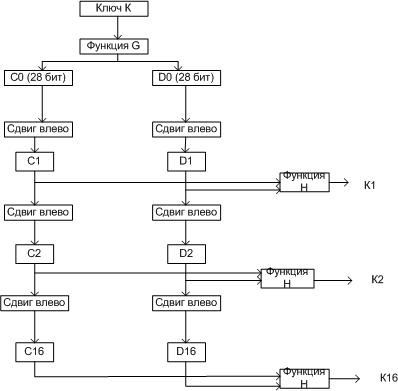
Схема алгоритма вычисления ключей Ki:
…..
После определения С0, D0 рекурсивно определяется до 16. Выполняется циклическая операция сдвига в лево на 1 или 2 бита в зависимости от шага итерации.
Таблица.
Номер итерации |
Количество si сдвигов влево бит |
Номер итерации |
Количество si сдвигов влево бит |
1 |
1 |
9 |
1 |
2 |
1 |
10 |
2 |
3 |
2 |
11 |
2 |
4 |
2 |
12 |
2 |
5 |
2 |
13 |
2 |
6 |
2 |
14 |
2 |
7 |
2 |
15 |
2 |
8 |
2 |
16 |
1 |
Общий ключ формируется функцией H, Ki=H(Ci Di), где функция Н определяется матрицей, завершающей обработку ключа.
Основные режимы работы алгоритма DES.
Алгоритм DES подходит как для шифрования так и для аутентификации данных. Он позволяет непосредственно преобразовывать 64-битовый входной открытый текст в 64 битовый выходной шифротекст. Однако данные редко ограничиваются 64 разрядами, для решения различных криптографических задач разработано 4 рабочих режима:
Электронная кодовая книга(ECB)
Сцепление блоком шифра (CBC)
Обратная связь по шифротексту (CFB)
Обратная связь по выходу (OFB)