
- •Основные этапы становления криптографии как науки
- •Простейшие шифры, их свойства. Шифры замены и перестановки.
- •3. Открытые сообщения и их характеристики.
- •4. Частотные характеристики открытых сообщений.
- •5. Критерии на открытые сообщения.
- •6. Основные понятия криптографии
- •7. Криптосистема, ключевая система шифра, основные требования к криптосистемам.
- •8. Шифр перестановки. Разновидности.
- •9. Криптоанализ шифров перестановки.
- •10. Шифр замены, одноалфавитные и многоалфавитные замены.
- •11. Вопросы криптоанализа простейших шифров замены.
- •12. Поточные шифры замены.
- •13. Табличное и модульное гаммирование. Случайные и псевдослучайные гаммы.
- •14. Криптограммы, полученные при повторном использовании ключа.
- •Вопрос 15. Математическая модель шифра. Опорный шифр.
- •Вопрос 16. Шифр с неограниченным ключом
- •Вопрос 17. Модель шифра с ограниченным ключом.
- •18. Шифры совершенные по Шенону.
- •19.Теоретическая стойкость шифра с позиции теории информации.
- •20. Безусловно и вычислительно стойкие шифры. Избыточность языка и расстояние единственности.
- •21. Имитостойкость шифра. Имитация и подмена сообщений.
- •22. Характеристики имитостойкости. Методы обеспечения имитостойкости.
- •23. Совершенная имитостойкость.
- •24. Линейные регистры сдвига
- •25. Помехоустойчивость шифров. Характеристики помехоустойчивых шифров.
- •26. Основные способы реализации криптографических алгоритмов и требования к ним.
- •27. Методы получения случайных и псевдослучайных последовательностей.
- •28. Методы анализа криптоалгоритмов. Понятие криптоатаки.
- •29. Методы анализа криптоалгоритмов. Перебор ключей
- •30. Методы анализа криптоалгоритмов. Метод встречи посередине.
- •31. Методы анализа криптоалгоритмов. Бесключевые методы.
- •32. Система шифрования с открытым ключом. Понятие односторонней функции с секретом.
- •33. Криптосистемы rsa.
- •34. Криптосистема Эль-Гамаля.
- •35. Проблема факторизации целых чисел и логарифмирование в конечных полях.
- •36. Американский стандарт шифрования des
- •37. Российский стандарт шифрования гост 28147-89
- •38. Шифр rc4
- •39. Шифр Rijndael. Математические основы работы.
- •40. Шифр Rijndael. Работа с байтами состояния.
- •41. Шифр Rijndael. Алгоритм выработки ключей.
- •43. Криптографические протоколы. Модели криптографических протоколов.
- •Классификация
- •44. Электронная цифровая подпись. Стандарты эцп.
- •45. Математические основы шифрсистем на эллиптических кривых.
- •46. Свойства множества точек эллиптической кривой.
- •47. Выбор параметров на эллиптической кривой. Шифр Эль-Гамаля на эллиптической кривой.
- •48.Эцп на базе эллиптической кривой.
- •49. Протоколы установления подлинности. Парольные системы разграничения доступа.Протокол рукопожатия.
- •50. Криптосистема на алгоритме а5
- •51. Протоколы сертификации ключей. Протоколы распределения ключей.
- •52. Протоколы выработки сеансовых ключей. Открытое распределение ключей Диффи-Хеллмана.
45. Математические основы шифрсистем на эллиптических кривых.
Нил Коблиц и В.Миллер в 1985г. Предложили использовать эллиптические кривые для ериптограф. Целей. В1998г. Исп-ие эллиптических кривых было закреплено в стандартах США ANSI Х.9.62, FIPS 186-2. В РФ ГОСТ З.34.10-2001.
Основное достоинство криптосистем на эллиптических кривых состоит в том, что по сравнению с обычными криптосистемами они обеспечивают существенно высокую стойкость при равной трудоемкости или меньшую трудоемкость при равной стойкости.
Это объясняется тем, что для вычисления обратных функций на эллиптических кривых известны только алгоритмы с экспоненциальным ростом трудоемкости. В то время как для обычных криптосистем предложены субъекспоненциальные методы.
Математические основы
Кривая 3го порядка Е, которая задается след.уравнением: y^2=x^3+ax+b (1) На самом деле, это уравнение получено путем замены более общего уравнения. Чтобы найти пересечение с осью н, необходимо решить уравнение: x^3+ax+b=0 (2) с помощью формул Кардана. Если ДЮ0,то имеется 3 действительных корня. Если Д=0, то (2)имеет 3 действительных корня и по крайней мере 2 из них равны. Если ДЮ0, то (2) имеет один действительный и 2 комплексносопряженных.
1.
Д<0![]() 2. Д=0
2. Д=0
![]()
3.
Д>0
![]()
Композиция точек P и Q
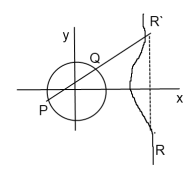
Прямая ч/з т. P и Q пересечет кривую в т. R`. Нарисуем т.R путем изменения знака ординаты т.R`.Эта операция называется композицией точек. Д=4а^3+27b^2.
Решение уравнения (1) совместно с бесконечно удаленной точкой задают множество точек кривой. Будем рассматривать эллиптическую кривую над простым полем р>3. Для числа точек N справедлива оценка, задаваемая теорией Хосе: |N-p|< 2√p. На кривой (1) определен инвариант : j=12^3*((4a^3)/(4a^3+27b^2)).
Для получения кривой с заданными инвариантами отличными от 0и 12:33 можно использовать следующее уравнение : y^2=x^3+3kr^2*x+2kr^3 (1a). На множестве точек воодиться структура абелевой группы с помощью закона сложения. Для сложения точек P(x1,y1) и Q(x2,y2) проводиться секущая , которая пересекает кривую в т.R`(x3,-y3). Тогда точка т.(x3,y3) по определению является суммой точек P и Q: R=P+Q.
46. Свойства множества точек эллиптической кривой.
Сложение точек.
P+(-P)= (точка на бесконечности)
(точка на бесконечности)
P=P+ , т.е. – нейтральный элемент.

Группа точек на кривой.
Точки на кривой вместе с (точка на бесконечности) и операцией сложения образуют коммутативную группу, т.е. для любых точек P и Q и Т на кривой выполняются свойства:
1.Сумма P и Q лежит на кривой или равна (замкнутость)
2.(А+В)+Т=А+(В+Т) – ассоциативность
3.P+Q=Q+P – коммутативность
4.P+Q=P – наличие нуля
5.Существует такая точка P, что Р+(-Р)= – наличие противоположного элемента.
Закон
сложения описывается следующими
формулами:
 ,
,
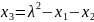 ,
,
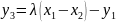 ,
где
,
где
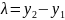 =
= ,
если P=Q.
,
если P=Q.
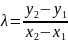 ,
если
,
если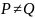 .
Если P=Q,
то R=P+P=[2]P.
R=[m]P.
.
Если P=Q,
то R=P+P=[2]P.
R=[m]P.
47. Выбор параметров на эллиптической кривой. Шифр Эль-Гамаля на эллиптической кривой.
В
криптографии неприменима вещественная
арифметика. Для перехода к условным
числам кривую рассматривают не на
обычной вещественной плоскости, где х,
у – вещественные числа, а на некотором
конечном поле, где х, у могут принимать
фиксированный конечный набор значений.
Для эллиптич. кривой Е используют поля (р – простое число) и
(р – простое число) и
 .
.
Поле Fp:
- Эл-ты поля – числа 0,1,2,…,n-1
- Все операции выполняются по модулю р
- Сумма х и у есть (х+у) mod p
- Произведение х и у есть х*у mod p
- Обратное к х есть такое число х-1 из Fp, что xx-1mod p=1
- Частное х и у есть xy-1 mod p
Кривая Fp
Уравнение рассматривают по модулю р.
yx3+ax+b (mod p)
Геометрическая интерпретация операции над точками такой кривой не удается.ю однако алгебраические формулы остаются верны, если выполнять вычисления по модулю р. Операции над точками сводятся к целочисленной модулярной арифметике.
Применение эллиптических кривых
1.Стороны должны договариваться об общем наборе параметров (domain parameters)
2.Для Fp: (p, a, b, G, n, h), где p-простое число, размер поля; a, b – коэф-ты уравнения кривой, G – точка на кривой (генератор, основание логарифма); n – такое число, что nG=0 (порядок кривой); h=E(Fp)/n – сомножитель, где E(Fp) – число точек на кривой
Для F2m: (m, f(x), a, b, G, n, h), где m – простое число (при составном – эллиптическая кривая уязвима к определенному типу атак), f(x) – несократимый (не раскладываемы на многочлены) многочлен степени m, играет роль модуля при операциях. Остальные параметры аналогичны Fp.
Шифр Эль-Гамаля на эллиптической кривой.
Для шифрования и дешифрования текстов, с помощью эллиптических кривых использовались несколько методов. Один из них состоит в том, чтобы моделировать криптосистему Эль-Гамаля, используя эллиптическую кривую в GF(p) или GF(2n), как это показано на рисунке
Генерация общедоступных и частных ключей
Боб выбирает E (a,b) с эллиптической кривой в GF(p) или GF(2n).
Боб выбирает точку на кривой, e1 (x 1, y1 ).
Боб выбирает целое число d.
Боб вычисляет
 .
Обратите внимание: умножение здесь
означает, что многократное сложение и
определяется как раньше.
.
Обратите внимание: умножение здесь
означает, что многократное сложение и
определяется как раньше.
Боб объявляет E (a,b), e1 (x1, y1 ) и e2 (x2, y2) как свой открытый ключ доступа; он сохраняет d как секретный ключ.
Шифрование
Алиса выбирает P, точку на кривой, как ее исходный текст, P. Затем она вычисляет пару точек, направляет как зашифрованный текст:
Читатель может задаться вопросом, как произвольным исходным
C1 = r × e1 C2 = P + r × e2
Текстом может быть точка на эллиптической кривой. Это одна из основных проблем в применении эллиптической кривой для моделирования. Алиса должна использовать алгоритм, чтобы найти непосредственное соответствие между символами (или блоками текста) и точками на кривой.
Дешифрование
Боб, после получения C1 и C2, вычисляет P, исходный текст, используя следующую формулу:
P = C2 – (d × C1) Знак "минус" здесь означает сложение с инверсией.
Мы можем доказать, что P, вычисленный Бобом, — тот же, что передан Алисой, как это показано ниже:
![]()
P, C 1, C2 и e2 — это точки на кривой. Обратите внимание, что результат сложения двух обратных точек на кривой — нулевая точка.
