69. Признаки Куммера и Раабе.

Т.(Пр-к Куммера).Пусть ∑an- знакаположительный ряд и 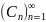-некотор посл-ть положит чисел, пусть далее K_n=C_n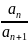 -C_n+1,n=1,2,… перемен Куммера для ряда ∑an постр по данной посл-ти (C_n), тогда: 1)Если такое δ>0, что начиная с некоторого номера K_n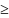 δ, то ряд ∑an сх-ся; 2)если начиная с некоторого номера 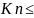0 и при этом ∑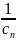 расх-ся, то ряд ∑an также расх-ся.

Т.(Пр-к Раабе).Пусть сущ-ет конечный или 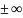предел R=lim n( -1), тогда: 1)при R>1 ряд сх-ся; 2)при R<1 ряд расх-ся; 3)при R=1 необх дополн исслед ряда.

70. Признаки Бертрана и Гаусса.

Т.(Пр-к Бертрана).Пусть для знакоположительного ряда ∑an сущ-ет конечный или предел B=lim B_n, B_n=(R_n-1)ln n, где R_n –переменная Раабе, тогда: 1)при B>1 ряд сх-ся; 2)при B<1 ряд расх-ся; 3)при B=1 необх дополн исслед ряда.

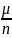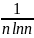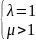Т.(Пр-к Гаусса). Пусть ∑an- знакаположительный ряд, пусть сущ-ют λ и μ такие, что отношение можно представить в виде: =λ+ +O( ) при n→+∞, тогда ряд ∑an: 1)сх-ся, λ>1 или ; 2)расх-ся, λ<1 или 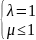; 3)сомнительных случаев нет.

71. Абсолютная сходимость числового ряда.

О. ∑an наз абсолютно сход-ся, если сх-ся ряд ∑|an| сост из модулей членов данного ряда(т.к |an |=an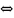 an 0, то для рядов понятие сх-ти совпадает с абсолютной сх-тью).

Т.Абсолютно сх-ся ряд ∑an сх-ся.

Т.Абсолютная сх-ть знакоперемен ряда равносильна сх-ти рядов, сост из его положительных и отрицательных членов.

72. Условная сходимость числового ряда.

О.Знакоперемен ряд ∑an наз условно сх-ся, если он сх-ся, но ряд из ∑|an| расх-ся.

Т.Если знакоперем ряд сх-ся условно, то ряды, сост из его положит и отриц чденов, расх-ся.

73. Знакочередующиеся ряды. Признак Лейбница.

Знакочеред ряд можно представить в виде:∑(-1)^n-1b_n=b1-b2+b3-…

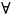Т.(Пр-к Лейбница)Пусть (b_n)-посл-ть положит чисел, монотонно →0, тогда: 1)знакочеред ряд сх-ся; 2)модуль любого остатка не превосходится модуля 1ого члена остатка: |∑(-1)^n-1b_n | b_n, nєN.

74. Преобразование Абеля. Неравенство Абеля. Следствие.

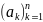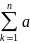Т.(Преобраз Абеля) Для любых конечных посл-тей и справедливы рав-ва: kbk=Anbn+ 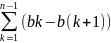Ak, где Ак=a1+…+ak.

Т.(Нер-во Абеля)Пусть -конечн убыв посл-ть полож чисел, или возраст посл отриц чисел, а для конечного числа посл-ти , постоян А такова, что |Ak|=|a1+…+ak|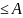 , k=1,…,n, тогда справедливо нер-во: |∑akbk| A*|b1|

75. Признаки Дирихле и Абеля для числовых рядов.

Т.(Пр-к Дирахле) Ряд ∑akbk сх-ся, если вып усл:1)Частичные суммы ряда ∑ak ограничены в совокупности; 2)посл-ть монотонно →0.

Т.(Пр-к Абеля) Ряд ∑akbk сх-ся, если вып усл: 1)ряд ∑ak сх-ся; 2) монтон и огранич.

76. Перестановки членов абсолютно и условно сходящихся рядов. Теорема Римана.

О.Принято говорить, ∑bn получ из исход ряда ∑an перестановками членов, если сущ-ет биективное отображение φ:N→N, такое что для любого kєN:bk=an, где k=φ(n).

Т.Если ∑an сх абсолютно, то ряд ∑bk, получ из исход перестановкой членов также сх-ся абсолютно к той же самой сумме.

Т.(Римана об усл сх-ти). Сущ-ет такая перестановка членов усл сх-ся ряда, что либо он окажется расх-ся, либо сумма получ ряда равна любому наперёд заданному числу, или .