13.Интегрирование дифференциальных биномов

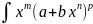
1)p€Z Привести m и n к общ знаменателю λ(m=m’/ λ, n=n’/ λ)

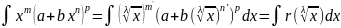Это инт-л от др-лин иррац => далее t=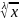

2)(m +1)/n € Z

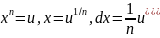
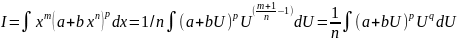, λ – знаменатель p.

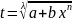
3)p+(m+1)/n € Z 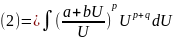. λ – знаменатель p.

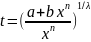
14. Понятие определённого интеграла Римана. Необходимое условие интегрируемости.

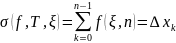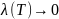Опр Ф-ия f:[a;b]->R наз-ся инт-ой в смысле Римана на отрезке [a;b], если сущ конечный предел I интегральных сумм при , т.е. 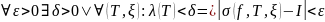. Этот предел наз-ся инт-лом Римана для f на [a;b] и обозн

Условие: Если функция интегрируется в смысле Римана на отрезке, то она ограничена на этом отрезке. НО не всякая ф-ия, ограниченная на отрезке, интегрируема на нем в смысле Римана.

15.Суммы Дарбу и их св-ва

Опр Нижней и верхней суммами Дарбу ф-ии f[a;b]->R, построенные для разбиения Т называются соответственно суммы

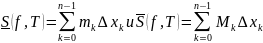
Св-ва:

1. 

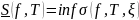
2. При измельчении разбиения Т нижняя сумма только увеличивается, верхняя – только уменьшается

3. Нижняя сумма не превосходит верхней, даже если они построены для разных разбиений

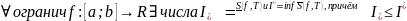4. (эти числа – верхн и нижн инт-лы от f[a;b]->R)

16.Критерий Дарбу.

Для интегрируемости ограниченной f[a;b]->R в смысле Римана на отрезке [a;b]  чтобы выполнялось условие 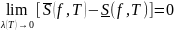или что тоже само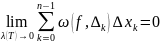е где 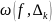- колебание функции на отрезке

17.Интегрируемость непрерывной функции.

Если функция непрерывна на отрезке, то она интегрируема на этом отрезке

18.Интегрируемость монотонной на отрезке функции

Если функция монотонна на отрезке, то она интегрируема на этом отрезке

19.Понятие о критерии Лебега.

Опр.Покрытие мн-ва Е – семейство мн-ва 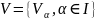, что EcV, т.е.

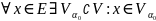
Опр.Мн-во счётное, если можно установить взаимооднознач соотношение между его элементами

Опр. Мн-во ЕcR имеет лебегову меру ноль, если 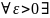такое покрытие мн-ва Е с конечным или счётным семейством интервалов, что сумма длин любого кол-ва интервалов

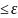
Т.Для того, чтобы огр ф-ия f:[a;b]->R была инт-ма в смысле Римана  чтобы мн-во всех её точек имело лебегову меру ноль.

Сл-вие Ф-ия, имеющая на отрезке конечное мн-во точек разрыва инт-ма в смысле Римана на это отрезке

Сл-вие Изменение значений ф-ии f:[a;b]->R на конечном мн-ве точек не влияет ни на инт-ость ф-ии, ни на величину

20.Линейность и монотонность интеграла Римана

Т(линейность) Если ф-ии 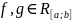то при 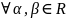их лин комбинация 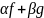также инт-на на [a;b]:

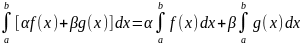
Т(монотонность) Если ф-ии , a<b и 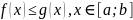, то вместе с тем и

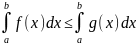
21.Аддитивность инт-ла Римама

Т(аддитивность) Если f by-на на [a;b], то 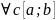она инт-на на [a;c] и [c;b]:

22.Интегрируемость модуля функции. Оценка интеграла.

Т(об инт-сти модуля) Есл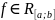и то и , причём модуль инт-ла не превосходит инт-ла модуля.

Сл-вие(оценка инт-ла) Если , то 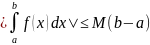, где

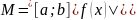
Замеч Если f непрер на [a;b], то

23.Интегрируемость произведения функций

Т(инт -ость произв ф-ий) Если , то и

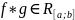
Т(оценка инт-ла от произв) Пусть выполнены усл:

1. , a<b

2. 

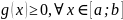
3. Для некот const m и M, ф-ия удовл нер-вам 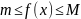, , 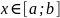тогда справедливы оценки: m .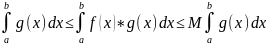

24.Первая теорема о среднем для интегралов

T. Пусть выполняется условие:

1)

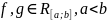
2) хотя бы одна функция (пусть g(x)) меняет знак на [a;b]

3)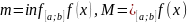 , тогда , то

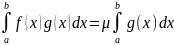
Причём кроме того, если f непрерывна на [a;b], то

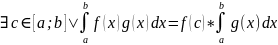
25.Формула Ньютона-Лейбница

Т. Если f:[a,b]->R интегрирована на [a,b] и на этом отрезке сущ первообразная F ф-ии f, то справедливо равенство:

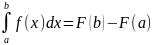
26.Существование первообразных

Т.Непрерывн на отр-ке ф-ия имеет первообразную на этом отр-ке.

Т.Пусть ф-ия f(x) инт-ма на [a;b], тогда инт-л с перемен верх пределом F(x)= явл ф-ей непрер на [a;b]

27.Замена переменной в определённом интеграле

Т. Пусть выполнены условия:

1) f – непрер на [a;b]

2) ф-ия непр, диф-ма на

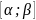
3)

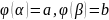
Тогда справедлива ф-ия замены переменной в опр инт-ле

Т. (усил вариант замены)Пусть выполняются условия:

1)

2) ф-ия непр, диф-ма и строго монотонна на

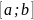
3) , тогда ф-ия 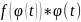также инт на

Тогда справедлива формула

28.Интегралы от чётных, нечётных и периодических функций. Интегрирование по частям.

T. Интеграл от чётной интегрируемой функции по симметричному относительно 0 прямоугольнику равен удвоенному интегралу по половине прямоугольника. А интеграл от нечетной функции равен 0:

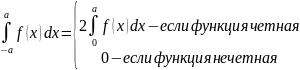
Т. Пусть f:R->R имеет период Т и интегрируема на каждом отрезке [a;b]cR, тогда интеграл от f по любому отрезку длины T сохраняет const значение:

Т. Пусть ф-ии U=U(x) и V=V(x) имеют на отрезке [a;b] инт-мые производные, тогда