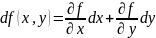- •1.Первообразная, неопределённый интеграл и их свойства.
- •13.Интегрирование дифференциальных биномов
- •14. Понятие определённого интеграла Римана. Необходимое условие интегрируемости.
- •29.Открытые и замкнутые множества в r2
- •36. Основные классы кривых
- •53.Достаточное условие дифференцируемости отображения в точке.
- •54. Производная по направлению.
- •55.Теорема Лагранжа оконечных приращениях
- •57.Локальный экстремум функций векторного аргумента. Необходимое условие.
- •58. Достаточное условие локального экстремума ф-ции вект. Аргумента (общий случай)
- •59. Теорема о существовании локального экстремума для функций двух переменных.
- •62.Условный экстремум. Необходимый и достаточный признаки существования.
- •63.Основные понятия числовых рядов.
- •64.Простейшие операции над рядами.
- •65. Критерий Коши и другие критерии сходимости для числовых рядов
- •66. Признаки сравнения для знакоположительных рядов.
- •69. Признаки Куммера и Раабе.
- •70. Признаки Бертрана и Гаусса.
29.Открытые и замкнутые множества в r2
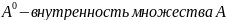
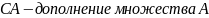
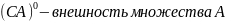
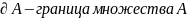 (граница – замкнутое
мн-во)
(граница – замкнутое
мн-во)
Опр Мн-во XcR2 наз-ся открытым в R2, если все точки внутренние, т.е. X=X0
Опр Т.М называется предельной для множества А, если в V ей окрестности U(M) есть беск мн-во точек из А. Предельная точка может принадл или не принадл мн-ву.
Опр
Мн-во YcR2
называется замкнутым в R2,
если его дополнение CY=
R2\Y
открыто в R2
или если содержит все свои предельные
точки
 – замыкание мн-ва А (мн-во А + все его
предельные точки)
– замыкание мн-ва А (мн-во А + все его
предельные точки)
Замкнутое мн-во совпадает со своим замыканием.
30.Квадрируемые фигуры
Опр
Нижняя площадь фигуры А -
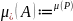 по всем P0
содержащ в A:P0
c
A
по всем P0
содержащ в A:P0
c
A
Опр
Верхняя площадь фигуры А -
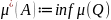 по всем
по всем
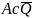

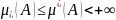
Опр
Фигура AcR2
наз-ся квадрируемой
, если её
нижняя и верхняя площади совпадают. В
этом случае
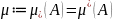
31. О критериях квадрируемости плоской фигуры
(1ый
кр. квадр)
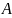 – квадрируема
– квадрируема

(2ой кр. квадр)
(3ий кр. квадр) Необх и дост, чтобы ее граница была фигура площади 0
32. Площадь криволинейной трапеции
Пусть f:[a;b]→R-неотриц ф-ия.Криволиненой трапецией наз мн-во A={(x,y)єR2:a x b; y=f(x)}
Т.Если f:[a;b]→R-неотриц инт-ма ф-ия, то криволинейная трапеция квадрируема и её площадь равна: μ(A)=
33.Площадь криволинейного сектора
Пусть
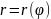 .
Криволинейным сектором наз. плоская
фигура
.
Криволинейным сектором наз. плоская
фигура
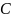 ,
которая в полярн. системе координат
может быть задана
,
которая в полярн. системе координат
может быть задана
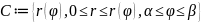 Если
,
то
Если
,
то
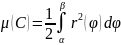
34. Вычисление объемов некоторых тел
Пусть
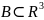 – тело, распол. между касающимися его
плоскостями
– тело, распол. между касающимися его
плоскостями
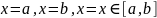 ,
- квадрир. Если
,
- квадрир. Если
 интегрируемо на
интегрируемо на
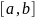 ,
то тело
,
то тело
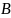 - кубируемо и его объем равен интегралу
- кубируемо и его объем равен интегралу
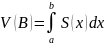
35. Основные понятия связанные с плоскими кривыми
Опр.
Плоской кривой в
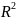 назы-ся любое непрерывное отображение
назы-ся любое непрерывное отображение
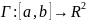 отрезка
или
отрезка
или
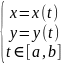 (1)
(1)
Опр. Две кривые
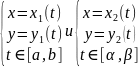
наз-ся
совпадающими, если
 непрер.
строго возраст ф-ция
непрер.
строго возраст ф-ция
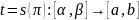
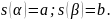
 ;
;
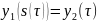
Опр.
Носителем (графиком) кривой (1) наз-ся
геом. образ этой кривой, т.е. мн-во точек
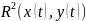 по всем
по всем
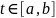
Опр.
Точки плоскости
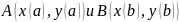 наз-ся началом и концом (1), если
наз-ся началом и концом (1), если
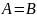 ,
то кривая наз-ся замкнутой, иначе
разомкнутой.
,
то кривая наз-ся замкнутой, иначе
разомкнутой.
Опр.
Точки
 , которым соотв.
, которым соотв.
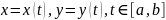 несколько точек
,
называются точками самопересечения
кривой, искл. случай
несколько точек
,
называются точками самопересечения
кривой, искл. случай
 – для замкнуто кривой.
– для замкнуто кривой.
36. Основные классы кривых
|Г| - носитель кривой Г
Опр
Кривая
называется простой или жордановой,
если
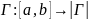 – взаимнооднозначн. (для замкн. кривой
–
– взаимнооднозначн. (для замкн. кривой
–
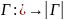
Опр Кривая наз-ся гладкой, если на непр. диф-ема на [a,b] и их произв. одновременно не обращ. в 0
Опр Кривая наз-ся кусочно гладкой, если [a,b] можно разбить на кон. число отрезков, каждая кривая на которых будет гладкой
Опр
Пусть
– нек. кривая,
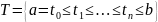 – разбиение отрезка [a,b], тогда ломаная
с паследоват. вершинами
– разбиение отрезка [a,b], тогда ломаная
с паследоват. вершинами
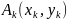 называется вписанной в кривую Г
называется вписанной в кривую Г
Опр
Кривая
называется спрямляемой, если множество
длин
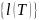 всевозможных ломанных вписанных в
кривую ограничено сверху. В этом случае
конечн. верхняя граница
всевозможных ломанных вписанных в
кривую ограничено сверху. В этом случае
конечн. верхняя граница
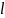 называется длиной кривой:
называется длиной кривой:
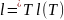 ,
где sup берется по всем разбиениям Т
[a,b]
,
где sup берется по всем разбиениям Т
[a,b]
37. Длина гладкой кривой. Спрямляемость кусочно-гладкой кривой
Т Гладкая кривая спрямляема, и для ее длины справедл. формула:
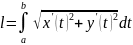
T Кусочно гладкая кривая спрямляема, и ее длину можно вычислить
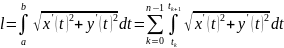
где
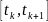 – отрезки, на которых кривая гладкая.
– отрезки, на которых кривая гладкая.
38. Площадь поверхности вращения
Опр
Поверхность
вращения графика ф-ции
 вокруг Ох наз-ся квадрируемой, если
мн-во
вокруг Ох наз-ся квадрируемой, если
мн-во
 площадей всех поверхносей ломаных
линий, вписанных в это графикограничено
сверху. Площадь фигуры вращения –
площадей всех поверхносей ломаных
линий, вписанных в это графикограничено
сверху. Площадь фигуры вращения –
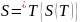
Если
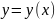 на [a,b]
имеет непрерывн произв, то
на [a,b]
имеет непрерывн произв, то
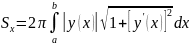
39.
Евклидово пространство в
 (основные
понятия)
(основные
понятия)
Опр
Пр-во
наз-ся декарт произв
 -штук),
т.е. мн-во всех упорядоченных наборов
-штук),
т.е. мн-во всех упорядоченных наборов
Опр Евклидово расстояние ( метрика ) в - функция
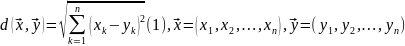
Теор ф-ла (1) удовлетв всем условиям метрики
Опр
Длиной
(евклидовой мерой) в-ра
 наз-ся число
наз-ся число
 где
где
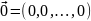 – начало координат в
– начало координат в
Опр
Скалярное
произведение векторов
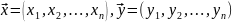 наз-ся число (
наз-ся число (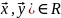
(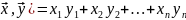
41. Основные топологические понятия в
Опр
Окрестностью
т.
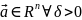 наз-ся мн-во
наз-ся мн-во
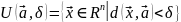 ,
,
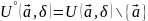
Опр
Мн-во
 наз-ся открытым, если оно содержит
каждую свою точку вместе с некоторой
окрестностью.
наз-ся открытым, если оно содержит
каждую свою точку вместе с некоторой
окрестностью.
Опр
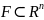 – замкн. если
– замкн. если
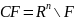 – открыто в
– открыто в
Опр
Мн-во
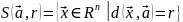 наз-ся сферой с центром в т.
наз-ся сферой с центром в т.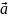 и радиусом
и радиусом
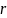 .
Замкнутое.
.
Замкнутое.
Опр
т.
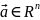 по отношению к мн-ву
наз-ся:
по отношению к мн-ву
наз-ся:
внутренней, если содерж в Е с некот своей окр-тью
внешней, если явл-ся внутренней для СЕ
граничной, если ни внутр, ни внешняя
предельной,
если
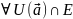 – бесконечн множество
– бесконечн множество
изолированной,
если
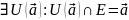
Опр
мн-во
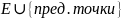 наз-ся замыканием мн-ва
наз-ся замыканием мн-ва
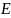 и обозначается
и обозначается
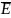
Теор
мн-во
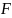 – замкнуто в
– замкнуто в
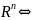
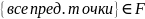
40. Сходимость в и его полнота
Опр
Посл-ть в-ров
из
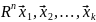 наз-ся сходящейся к вектору
,
если
наз-ся сходящейся к вектору
,
если
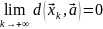

Теор Сходимость посл-ти векторов равносильно их покоординатной сх-ти:
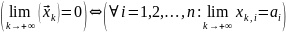
Теор(крит
Коши) Посл-ть
в-ров
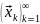 сх-ся в
тогда и только тогда, когда она
фундаментальна:
сх-ся в
тогда и только тогда, когда она
фундаментальна:

Следств Евклидово пр-во явл-ся полным.
42. Кратные пределы отображений. Теорема о покоординатной сходимости
Опр
Пусть
- предельная точка
.
Принято говорить, что
 ,
явл-ся пределом
,
явл-ся пределом
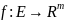 в т.
по мн-ву
,
если вып-ся одно из условий:
в т.
по мн-ву
,
если вып-ся одно из условий:
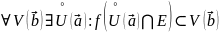

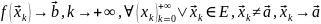
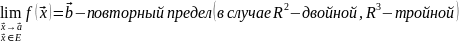
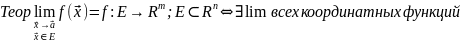
43. Повторный предел. Теорема о существовании повторного предела.
Повторными
пределами для
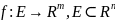 в точке
в точке
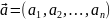 ,
предельной для Е, наз-ся пределы по
мн-ву Е вида:
,
предельной для Е, наз-ся пределы по
мн-ву Е вида:
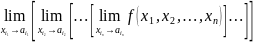
Теор
(о сущ-ии повтор предела) Пусть
для скалярной ф-ий 2-х перемен в некоторой
точке
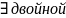 интеграл, а также предел по одной из
переменных, тогда в этой точке сущ-ет
и соотв двойной предел.
интеграл, а также предел по одной из
переменных, тогда в этой точке сущ-ет
и соотв двойной предел.
44.Непрерывность
отображений из
в
 .
Локальные свойства.
.
Локальные свойства.
Опр
Ф-ция
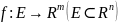 – непрерывна в точке
– непрерывна в точке
 ,
если
,
если
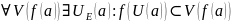
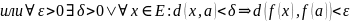
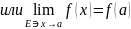
Локальные свойства:
- непрер
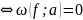
, непрерывное в т. , ограничено в некоторой
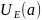
Если g
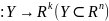 – непрерывно в
– непрерывно в
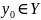 ,
a
,
a
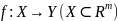 - непрерывно в
- непрерывно в
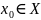 ,
причем
,
причем
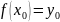 ,
то определено отображение
,
то определено отображение
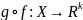 и оно непрерывно в точке
.
и оно непрерывно в точке
.
45.Глобальные свойства непрерывных отображений
1)
Если отображение
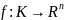 - непрерывно на компакте
- непрерывно на компакте
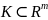 ,
то оно равномерно непрерывно на
,
то оно равномерно непрерывно на
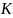 .
.
2) Если отображение - непрерывно на компакте , то оно ограничено на
3) Если ф-ция - непрерывна на компакте , то она принимает в некоторых точках мин. и макс. из своих значений на .
4)
Если ф-ция
- непрерывна на связном мн-ве Е,
принимает в точках
 значения
значения
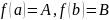 ,
то
,
то
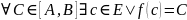 .
.
46.Линейные отображения из Rn в Rm.
Линейное отображение векторного пр-ва Х в Y наз-ся линейным над полем R, если:
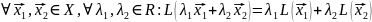
Т.
Отображение
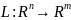 линейно т. и т. т., когда линейными явл-ся
все его коорд ф-ии.
линейно т. и т. т., когда линейными явл-ся
все его коорд ф-ии.
Т.
Для любого линейного
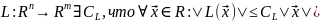
Линейное
отобр
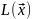 непрер в любой точке
непрер в любой точке
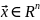
47 Дифференцируемые отображения из Rn в Rm. Простейшие свойства
Опр
Отобр
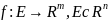 ,
называется дифф-мым в точке
,
называется дифф-мым в точке
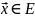 ,
если для него сущ-ет такое отображение
,
если для него сущ-ет такое отображение
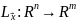 ,
что
,
что
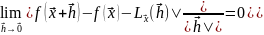
Св-ва:
1) Если отобр диф-мо в т. , то его производная опр-ся однозначно
2) Если отобр диф-мо, то оно непрерывно в этой точке
48.Дифференцируемость композиции отображений.
Пусть
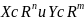 – откр мн-ва. Пусть далее f:X->Y
диф в точке
– откр мн-ва. Пусть далее f:X->Y
диф в точке
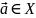 ,
а отобр g:Y->Rp
диф-мо в т.
,
а отобр g:Y->Rp
диф-мо в т.
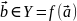 .
Тогда композиция g
o
а диф-ма в т.
и справедл рав- во:
.
Тогда композиция g
o
а диф-ма в т.
и справедл рав- во: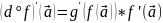
49.Теорема о покоординатной дифференцируемости отображения
Диф-ость
отобр
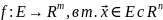 равнос диф-сти всех его покоорд ф-ий
fk,
причём справ-во покоординатное
представление диф-ла отобр:
равнос диф-сти всех его покоорд ф-ий
fk,
причём справ-во покоординатное
представление диф-ла отобр:
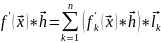 ,
где
,
где
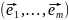 – стандартный базис в
.
– стандартный базис в
.
50.Частные производные. Теорема о смешанных производных.
ОПР
Частной произв 1го порядка скал ф-ии
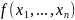 по переменной
по переменной
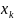 в т.
в т.
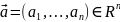 наз-ся обыкновен произв ф-ии
наз-ся обыкновен произв ф-ии
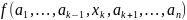 в т.
в т.
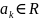 ,
т.е. предел:
,
т.е. предел:
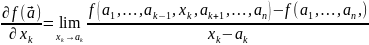
Т.
(о смешанных
произв) Если смешанные частные производные
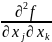 и
и
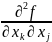 сущ в некот окр-сти в т.
и
непр-ны в самой т.
,
то они совпадают в этой точке, т.е.
сущ в некот окр-сти в т.
и
непр-ны в самой т.
,
то они совпадают в этой точке, т.е.
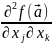 =
=
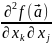
51.Матрица Якоби. Необходимое условие дифференцируемости отображения в точке.
 Если m =n,
то опред этой м-цы – якобиан.
Если m =n,
то опред этой м-цы – якобиан.
Если m=1, то м-ца Якоби – это в-ор. Этот вектор – градиент скал ф-ии вект аргумента.
T.
(необх усл диф-сти отобр в т.) Если
отображение
диф-мо в т.
 ,
то существует его матрица Якоби и она
совпадает с м-цей
,
то существует его матрица Якоби и она
совпадает с м-цей
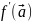 лин оператора
лин оператора
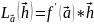 по опр диф-сти f
в т.
.
по опр диф-сти f
в т.
.
52. Диф-ал скалярной ф-ции
Если
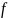 – скалярн. ф-ция, то диф-ал записывается
в виде
– скалярн. ф-ция, то диф-ал записывается
в виде
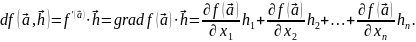
 обозначают
обозначают
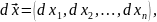 поэтому
поэтому
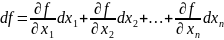 .
Для 2-х переменных
.
Для 2-х переменных