Проективная прямая и ее уравнение.

Пусть на проективной прямой дан репер R и взяты 2 точки: А (a₁, a₂, a₃) и В (b₁, b₂, b₃) принадлежащие прямой. Запишем уравнение этой прямой при условии, что М (х₁, х₂, х₃) –текущая точка, лежащая на прямой.

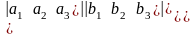– уравнение прямой линии.

Теорема: Фигура на проективной плоскости, заданная в проективном репере однородным уравнением первой степени u₁x₁ + u₂x₂ + u₃x₃= 0 есть прямая, где

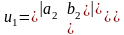
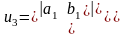
Доказательство:

Пусть γ - линия, заданная уравнением u₁x₁ + u₂x₂ + u₃x₃ = 0 u₁≠0

Уравнению удовлетворяют координаты двух точек: P (-u₂, u₁, 0)

Q (-u₃, 0, u₁)

Запишем условие принадлежности трех точек одной прямой:

где М (х₁, х₂, х₃) –текущая точка, лежащая на прямой.

Раскрыв определитель, получаем уравнение:

u₁²x₁ + u₁u₃x₃ + u₁u₂x₂ = 0, или

u₁x₁ + u₃x₃ + u₂x₂ = 0

Уравнение фигуры совпадает с уравнением прямой, отсюда следует, что фигура есть прямая линия.

Числа d (u₁, u₂, u₃)_R –называются координатами прямой d. ■

Взаимное расположение проективных прямых.

1. прямые u₁x₁ + u₂x₂ + u₃x₃ = 0 и v₁x₁ + v₁x₂ + v₃x₃ = 0 совпадают, если .

2. прямые u₁x₁ + u₂x₂ + u₃x₃ = 0 и v₁x₁ + v₁x₂ + v₃x₃ = 0 пересекаются, если ..

В проективной геометрии понятие координат точек и координат прямой обладает аналогичными свойствами: это объясняется принципом двойственности: «если справедливо утверждение Δ, в котором говорится о точках и прямых на плоскости и об их взаимном расположении, то справедливо и двойственное предложение Δ* которое получается из Δ заменой слова «точка» словом «прямая», а слова «прямая» словом «точка».

Пример: Δ= «Каждой прямой принадлежит бесконечное множество точек», Δ*= «Каждой точке принадлежит бесконечное множество прямых» (Через каждую точку проходит бесконечное множество прямых). Если справедливо исходное утверждение, то справедливо и ему двойственное.

Аналогичный принцип двойственности существует и в пространстве, причем слово «точка» заменяется словом «плоскость», а «плоскость» - «точка», а прямая остается прямой.

. Сложное отношение четырёх точек

Пусть на проективной прямой заданы точки: А, В, С, D, так, что точки А, В и С различные, а точка D не совпадает с точкой А.

Рассмотрим репер R₀=(А, В, С) и обозначим координаты точки D (х₁,х₂)_R , т.к. D не совпадает с т. А, то х₂≠0.

Число обозначаемое (АВ, СD)=х₁/х₂ называется сложным отношением четырёх точек.

Теорема: Координатное представление сложного соотношения четырёх точек.

Пусть в проективном репере т. А, В, С, D имеют координаты А(а₁, а₂), В(b₁, b₂), С(c₁, c₂), D(d₁, d₂), тогда

Свойства сложного отношения четырёх точек.

1. (АВ, СD)=1/ (AB, DC), (АВ, СD)=1/(ВА, DС)

2. (АВ, CD)=(BA,DC)

3. (АВ, СD)=(СD, АВ)

4. (АВ, СС)=1, (АВ, СВ)=0

5. (АВ, СD) + (АС, ВD)=1

Доказательство проводится на основе определения сложного отношения при учете, что рассматривается репер (А, В, С), где А(1, 0), В(0, 1), С(1, 1).

Зная сложное отношение четырёх точек А, В, С, D, можно найти сложное отношение всевозможных комбинаций этих точек.

Говорят, что точки А, В гармонически разделяют точки С, D, если (АВ, СD)=-1.