
- •Вопрос 8. Линии второго порядка, их канонические уравнения, фокусы, директрисы., асимптоты.
- •Вопрос 9. Прямая и плоскость в пространсте., их уравнения. Взаимное расположение прямых и плоскостей.
- •Взаимное расположение прямой и плоскости
- •Вопрос 10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •Проективная прямая и ее уравнение.
- •Линии второго порядка на проективной плоскости
- •Вопрос 11. Операции над векторами
- •2) C перпендикулярен к плоскости векторов а и b, если они приведены к общему началу.
- •Обозначается ab или a, b .
- •Вопрос 25. Задача потребительского выбора.
- •Вопрос 26. Понятие эластичности, геометрический смысл. Свойства эластичности.
- •Вопрос 27. Производственная функция. Закон убывающей эффективности.
- •Вопрос 29. Задача линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •Алгоритм решения задач
- •Вопрос 30. Нелинейное программирование
- •Вторая часть. Информатика.
- •Вопрос 25. Теория вычислительных погрешностей.
- •2) Если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности:
- •Вопрос 26. Нечеткие вычисления.
- •Примеры нечетких множеств
- •Нечеткие отношения
- •3. Правила записи приближенных чисел
- •Погрешность метода определяется третьей причиной, причем появление этой погрешности практически неизбежно при любых вычислениях.
- •2) Если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности:
- •3. Правила записи приближенных чисел
- •Примеры решения задач
- •Основные характеристики нечетких множеств
- •Примеры нечетких множеств
- •О методах построения функций принадлежности нечетких множеств
- •Свойства операций и .
- •Нечеткие отношения
- •Нечеткая и лингвистическая переменные
Примеры решения задач
Задача
1. Даны координаты вершин
 .
.
 ,
,
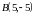 ,
,
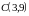 .
.
Найти:
1)
длину стороны
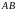 ;
;
уравнения прямых и
 и их угловые коэффициенты;
и их угловые коэффициенты;
угол
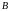 ;
;уравнение прямой, содержащей высоты
 и ее длину;
и ее длину;уравнение прямой, содержащей медианы
 и координаты точки
и координаты точки
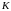 пересечения этой медианы с высотой
;
пересечения этой медианы с высотой
;уравнение прямой, проходящей через точку параллельно стороне ;
координаты точки
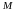 ,
расположенной симметрично точке
,
расположенной симметрично точке
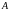 относительно прямой
.
относительно прямой
.
Решение:
Расстояние между точками
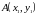 и
и
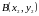 определяется по формуле:
определяется по формуле:
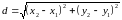 .
Значит, длина стороны
.
Значит, длина стороны
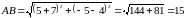 .
.
Уравнение прямой, проходящей через две точки и имеет вид:
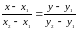 .
Подставляя в равенство координаты
данных точек, получим уравнения прямых
и
.
Подставляя в равенство координаты
данных точек, получим уравнения прямых
и
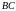
:
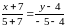 :
:
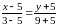
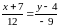

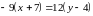
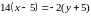
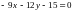
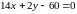
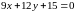
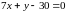
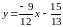
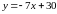
Получили
уравнения прямых линий с угловым
коэффициентом, из которых имеем:
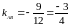 ;
;
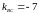 .
.
Тангенс угла
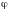 между двумя прямыми, угловые коэффициенты
которых соответственно равны
между двумя прямыми, угловые коэффициенты
которых соответственно равны
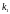 и
и
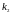 ,
вычисляется по формуле:
,
вычисляется по формуле:
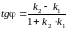 .
.
Угол располагается при пересечении прямых и , значит,
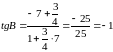 ;
=135
;
=135
4.
Высота
проходит через точку
и перпендикулярна прямой
.
Значит, нормальный вектор

прямой
является
направляющим вектором
 для прямой
.
для прямой
.
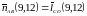
Уравнение
прямой, проходящей через точку
и имеющей направляющий вектор
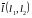 :
:
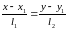
Значит, уравнение прямой :
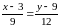
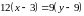

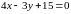
Для
того, чтобы найти длину высоты
,
необходимо определить координаты точки
 – точки пересечения прямых
и
.
Для этого надо решить систему уравнений:
– точки пересечения прямых
и
.
Для этого надо решить систему уравнений:
:
:
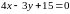
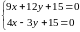
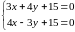
В
результате вычислений получены координаты
точки
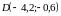 .
.
Чтобы найти уравнение прямой, содержащей медианы , определим сначала координаты точки
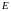 как середину стороны
,
применяя формулы, характеризующие
деление отрезка пополам:
как середину стороны
,
применяя формулы, характеризующие
деление отрезка пополам:
 ;
; 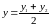
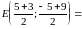
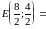

Тогда уравнение прямой :
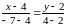


И, наконец, координаты точки находятся при решении системы уравнений:
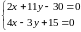
 ;
;
 .
.
Если две прямые параллельны, то можно сказать, что их уравнения отличаются только свободным членом. Значит, уравнение прямой, параллельной стороне , будет:
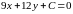
Известно,
что эта
прямая проходит через точку
эта
прямая проходит через точку
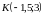 ,
значит, координаты точки должны
удовлетворять уравнению искомой прямой:
,
значит, координаты точки должны
удовлетворять уравнению искомой прямой:
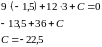
И тогда уравнение прямой будет иметь вид:
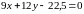 или
после деления на 3:
или
после деления на 3:
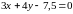
По условию точка симметрична точке относительно высоты , то есть точка является серединой отрезка
 .
Воспользуемся уже известными формулами
для определения координат середины
отрезка:
.
Воспользуемся уже известными формулами
для определения координат середины
отрезка:
;
;
 .
.
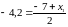 и
и 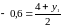
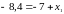
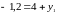
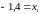

Значит,
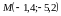 .
.
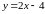 и
и
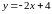 .
.
Задача 2.
Даны
вершины пирамиды:
 ,
,
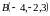 ,
,
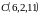 ,
,
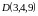 .
Необходимо найти:
.
Необходимо найти:
длину стороны
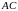 ;
;площадь грани
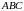 ;
;угол
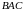 ;
;уравнение прямой ;
уравнение плоскости грани ;
уравнение высоты, опущенной из точки на грань , и ее длину;
точку, симметричную точке относительно грани ;
объем пирамиды.
Решение:
Длина стороны вычисляется по известной формуле:
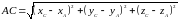
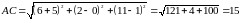 .
.
Для нахождения площади грани следует воспользоваться формулой, выражающей геометрический смысл векторного произведения:
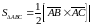
В нашей задаче
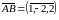

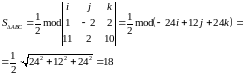
Угол
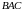 равен
равен

В пространстве уравнение прямой, проходящей через две точки
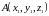 и
и
 ,
имеет следующий вид:
,
имеет следующий вид:
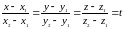 ,
где t
– некоторый параметр.
,
где t
– некоторый параметр.
Тогда уравнения прямой можно записать так:
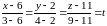
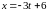 ,
,
 ,
,
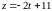 .
.
Плоскость грани можно описать как плоскость, проходящую через три точки ,
 ,
,
 и имеющую уравнение
и имеющую уравнение

Подставляя координаты точек и вычисляя определитель, получим уравнение грани :
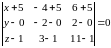
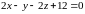
Каноническое уравнение прямой в пространстве, заданной точкой
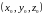 и направляющим вектором
и направляющим вектором
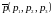 имеет вид:
имеет вид:

По
условию, прямая (высота), проходит через
точку
и перпендикулярна грани
.
Значит, вектор нормали к плоскости
будет являться направляющим вектором
искомой прямой.
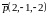
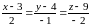
Чтобы
найти длину высоты, можно воспользоваться
формулой для нахождения расстояния от
точки
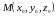 до плоскости
до плоскости
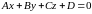 :
:
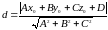
В
нашей задаче точка имеет координаты
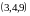 ,
а уравнение плоскости:
,
а уравнение плоскости:
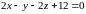
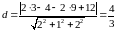 .
.
Найдем координаты точки пересечения высоты, опущенной из точки на грань , с самой гранью. Для этого запишем уравнения высоты в параметрическом виде и, подставив выражения
 ,
,
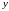 ,
,
 через параметр в уравнение плоскости
,
найдем значение параметра
через параметр в уравнение плоскости
,
найдем значение параметра
 :
:
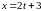 ,
,
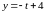 ,
,
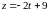

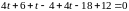 .
.
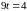
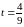
Подставив в параметрическое уравнение высоты, найдем координаты точки :
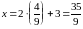
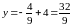
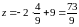 ;
; 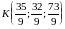
Пусть
 – точка, симметричная точке
относительно грани
,
тогда точка
– середина отрезка
– точка, симметричная точке
относительно грани
,
тогда точка
– середина отрезка
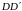 .
Подставляя координаты точек в известные
формулы для определения координат
середины отрезка, получим координаты
точки
:
.
Подставляя координаты точек в известные
формулы для определения координат
середины отрезка, получим координаты
точки
:
 ,
,
 ,
,
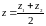
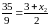 ,
,
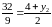 ,
,

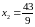 ,
,
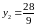 ,
,
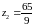
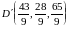 .
.
Объем пирамиды следует рассчитать по формуле, выражающей геометрический смысл смешанного произведения векторов:

Задача
3.
Даны координаты точек:
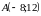 и
и
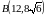 .
Требуется:
.
Требуется:
составить уравнение гиперболы, проходящей через эти точки, если ее фокусы расположены на оси
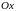 ;
;найти полуоси, эксцентриситет, фокусы;
написать уравнение гиперболы в полярной системе координат;
найти уравнения директрис и асимптот;
написать уравнения касательных к гиперболе в точке
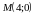 ,
в точке
,
в точке
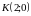 .
.
Решение:
Каноническое уравнение гиперболы имеет вид
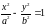 .
По условию, точки
и
лежат на гиперболе, следовательно, их
координаты удовлетворяют уравнению
гиперболы. Подставляя в уравнение
координаты данных точек, получим систему
двух уравнений относительно неизвестных
.
По условию, точки
и
лежат на гиперболе, следовательно, их
координаты удовлетворяют уравнению
гиперболы. Подставляя в уравнение
координаты данных точек, получим систему
двух уравнений относительно неизвестных
 и
и
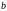 .
.

Решая
систему, например, способом сложения,
получим: и
и
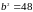 .
И тогда искомое уравнение имеет вид:
.
И тогда искомое уравнение имеет вид:
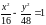 .
.
Полуоси гиперболы – это числовые значения a и b:
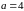 и
и
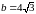 .
Координаты фокусов гиперболы,
расположенных на оси
,
определяются таким образом:
.
Координаты фокусов гиперболы,
расположенных на оси
,
определяются таким образом:
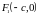 и
и
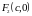 ,
где
,
где
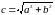 :
:
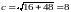 .
Значит, координаты фокусов данной
гиперболы:
.
Значит, координаты фокусов данной
гиперболы:
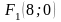 ,
,
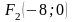 .
.
Эксцентриситет
гиперболы – это число
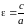 .
Определяем его:
.
Определяем его:
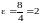 .
.
В полярной системе координат уравнение гиперболы имеет вид:
 .
.
Подставляем известные значения:
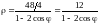 .
.
Директрисы гиперболы имеют уравнения
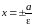 ,
в данном случае это будут прямые
,
в данном случае это будут прямые
 и
и
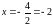 .
.
Прямые,
заданные уравнениями
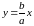 и
и
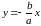 ,
называются асимптотами гиперболы; в
данной задаче уравнения имеют вид:
,
называются асимптотами гиперболы; в
данной задаче уравнения имеют вид:
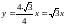 и
и
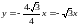 .
.
Уравнение касательной к гиперболе, заданной уравнением
 ,
в точке
,
в точке
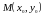 ,
лежащей на гиперболе, имеет вид:
,
лежащей на гиперболе, имеет вид:
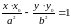 .
Для
.
Для
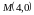 оно таково:
оно таково:
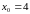 .
.
Точка
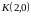 не принадлежит гиперболе. Уравнение
касательной можно записать в виде
не принадлежит гиперболе. Уравнение
касательной можно записать в виде
 (так как касательная – это прямая линия).
Точка
лежит на касательной, значит, ее координаты
удовлетворяют уравнению этой прямой:
(так как касательная – это прямая линия).
Точка
лежит на касательной, значит, ее координаты
удовлетворяют уравнению этой прямой:
 ;
;
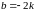 .
.
И
тогда уравнение касательной будет
следующим:
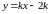 .
Касательная и гипербола имеют единственную
общую точку. Попробуем решить систему
уравнений:
.
Касательная и гипербола имеют единственную
общую точку. Попробуем решить систему
уравнений:
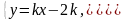

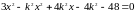 ,
,
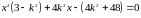 .
.
Вычисляем дискриминант квадратного уравнения:
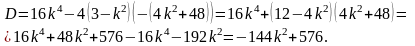
Так
как прямая и гипербола имеют одну общую
точку, то это уравнение имеет единственное
решение и
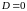 :
:

Значит, касательные задаются уравнением и .
Задача 4. Определить вид заданной линии второго порядка, найти ее центр, векторы оси асимптотического направления, главные направления и главные диаметры.
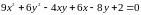 .
.
Решение:
Для определения вида заданной линии второго порядка упростим общее уравнение линии, чтобы свести к каноническому. Такое упрощение достигается при переходе к канонической системе координат посредством поворота осей системы на определенный угол и переноса начала в нужную точку.
Поворот
осей исходной системы
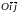 необходим лишь при присутствии в
уравнении линии слагаемого, содержащего
произведение
необходим лишь при присутствии в
уравнении линии слагаемого, содержащего
произведение
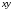 ,
и он реализуется на такой угол, чтобы
уравнение линии в новой системе координат
,
и он реализуется на такой угол, чтобы
уравнение линии в новой системе координат
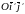 не содержало произведения. Такая система
координат всегда присутствует, а
направления осей этой системы называются
главными направляющими линии II
порядка.
не содержало произведения. Такая система
координат всегда присутствует, а
направления осей этой системы называются
главными направляющими линии II
порядка.
В полученном после соответствующих преобразований уравнении необходимо выделить полные квадраты и реализовать перенос начала полученной системы координат.
Таким образом, реализуется двойной переход:
1) от системы к системе ;
2)
от системы
к системе
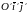 .
.
Единичные векторы главных направлений линии имеют координаты
 ,
,
 .
.
Для их нахождения, а, следовательно, для упрощения уравнения заданной линии используем общую схему приведения уравнения линии II порядка к каноническому виду.
Решаем характеристическое уравнение данной линии:
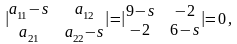
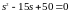 .
.
Его
корни
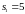 и
и
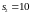 .
.
Находим угловые коэффициенты главных направлений:
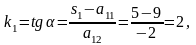
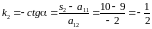 .
.
Из курса тригонометрии известны формулы
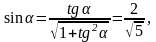
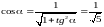 .
.
Найдем координаты векторов и :
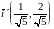 и
и
 .
.
Очевидно,
что наша линия второго порядка
поворачивается на угол
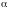 .
Преобразования координат при повороте
на угол
будут следующими:
.
Преобразования координат при повороте
на угол
будут следующими:
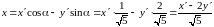 ,
,
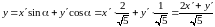 .
.
В новой системе координат уравнение принимает вид:
 ,
,
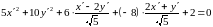 ,
,
 ,
,
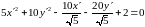 .
.
Выделяя полные квадраты и преобразовывая, получаем уравнение эллипса в системе координат :
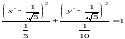 .
.
Координаты
нового начала координат
 – центра линии II
порядка – в системе
следующие:
– центра линии II
порядка – в системе
следующие:
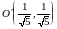 .
Для нахождения координат центра линии
в исходной системе координат
необходимо решить систему уравнений:
.
Для нахождения координат центра линии
в исходной системе координат
необходимо решить систему уравнений:

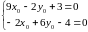 .
Центр имеет координаты
.
Центр имеет координаты
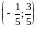 .
.
Вектор
асимптотического направления должен
иметь координаты
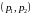 ,
удовлетворяющие условию:
,
удовлетворяющие условию:
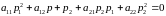 ,
,
 .
.
Для
удобства выберем угловой коэффициент
прямой асимптотического направления
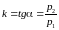 ,
получим уравнение
,
получим уравнение
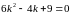 ,
которое не имеет корней, значит, у данной
линии асимптотических направлений нет,
что и должно быть: эллипс не имеет
асимптотических направлений. Необходимым
и достаточным условием главного
направления
,
которое не имеет корней, значит, у данной
линии асимптотических направлений нет,
что и должно быть: эллипс не имеет
асимптотических направлений. Необходимым
и достаточным условием главного
направления
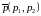 является условие
является условие
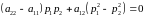 ,
,
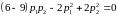 ,
,
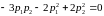 .
.
Пусть
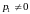 и
и
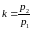 – угловой коэффициент главного
направления,
– угловой коэффициент главного
направления,
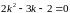
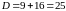
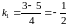 ,
,
 .
.
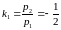 ,
значит, первый вектор главного направления
имеет координаты
,
значит, первый вектор главного направления
имеет координаты
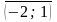 ,
аналогично
,
аналогично
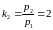 вторым вектором будет вектор
вторым вектором будет вектор
 .
.
Главные диаметры описываются уравнениями:
 ,
,
 :
–
:
–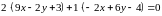 ,
,
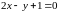 ,
,
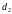 :
:
 ,
,
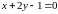 .
.
З адача 5. Привести к каноническому виду уравнение поверхности второго порядка, определить координаты ее центра и уравнения прямолинейных образующих
 .
.
Решение:
Характеристическое уравнение поверхности второго порядка можно задать с помощью определителя следующего вида:
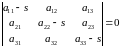 ,
,
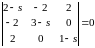 .
.
Разложим
определитель по элементам первой строки
и, после приведения подобных, получим
кубическое уравнение
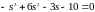 .
.
Его
корни
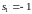 ,
,
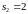 ,
,
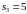
Найдем
главные направления, решая для каждого
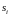
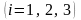 систему вида:
систему вида:
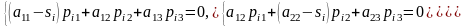
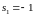 ;
;
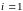 :
:
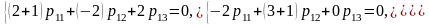
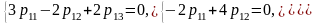

Из
третьего уравнения системы видно, что
первая координата вектора
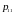 может принимать любое значение. Возьмем
для простоты
может принимать любое значение. Возьмем
для простоты
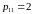 ,
тогда вектор главного направления при
будет иметь координаты
,
тогда вектор главного направления при
будет иметь координаты
 .
.
Аналогичные
вычисления производятся при
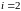
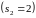 и
и
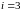
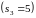 .
.
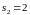 ,
:
,
:
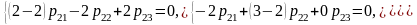
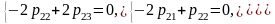

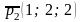 – второй
вектор.
– второй
вектор.
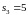 ,
:
,
:
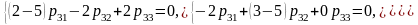
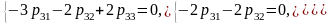

 – третий
вектор.
– третий
вектор.
Базис
 должен быть ортонормированным, поэтому
координатные единичные векторы новой
системы координат имеют координаты
должен быть ортонормированным, поэтому
координатные единичные векторы новой
системы координат имеют координаты
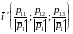 ;
;
 ;
;
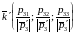 .
.
В нашей задаче:
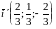 ;
;
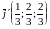 ;
;
 .
.
В новой системе координат данная поверхность имеет уравнение:
 ,
,
где
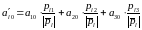 (
(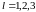 ).
).
Имеем:
1)
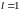 :
:
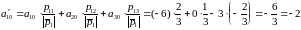 .
.
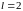 :
:
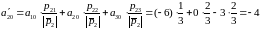 .
.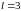 :
:
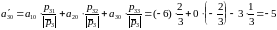 .
.
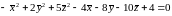 .
.
Выделяя полные квадраты и преобразовывая, получаем уравнение поверхности в новой системе координат:

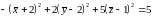
 .
.
В
результате вычислений получили уравнение
однополостного гиперболоида в системе
координат
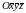 .
.
Составим уравнения семейства прямолинейных образующих этой поверхности:
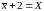 ,
,
 ,
,
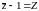 ,
,
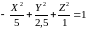 ,
,
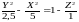 ,
,
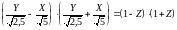 .
.
У однополостного гиперболоида есть 2 семейства прямолинейных образующих, они имеют вид:
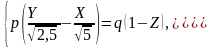 и
и

И,
наконец, найдем центр поверхности: в
системе координат
это будет точка
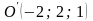 .
Центр поверхности в системе координат
.
Центр поверхности в системе координат
 определяется как решение системы
уравнений:
определяется как решение системы
уравнений:
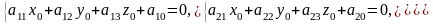
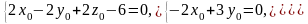
Искомая
точка имеет координаты
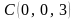 .
.
Задача 6. Привести к нормальному виду методом Лагранжа и найти соответствующий канонический базис квадратичной формы
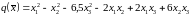 ,
,
заданной
в базисе
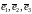 пространства
пространства
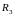 .
.
Решение:
В
векторном пространстве
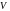 всегда существует такой базис, в котором
данная квадратичная форма имеет
нормальный вид:
всегда существует такой базис, в котором
данная квадратичная форма имеет
нормальный вид:
 .
.
Для решения задачи приведения формы к нормальному виду воспользуемся, согласно требованию задачи, методом Лагранжа. Идея этого метода заключается в том, что, выполняя алгебраические преобразования, квадратичную форму приводят к виду:
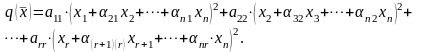
Далее,
вводя новые переменные
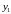 ,
,
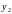 ,
...
,
...
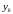 ,
,
 ,
... ,
,
... ,
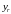 эту форму записывают в более компактном
виде.
эту форму записывают в более компактном
виде.
Решение
этой задачи начнем с того, что сгруппируем
все члены, содержащие
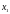 ,
и дополним их до полного квадрата.
,
и дополним их до полного квадрата.
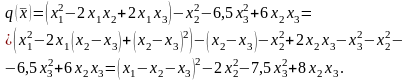
Аналогично
поступаем с членами, содержащими
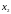 и
и
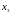 :
:
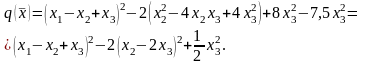
Далее рассмотрим следующее преобразование переменных соответственно базисных векторов:
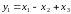 ,
, 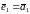 ,
,
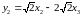 ,
, 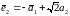 ,
,
 ,
, 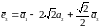 .
.
В
новом базисе
 ,
,
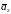 ,
,
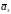 форма
форма
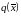 имеет нормальный вид
имеет нормальный вид
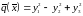 .
.
Векторы
соответствующего канонического базиса
в старом базисе
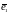 ,
,
 ,
,
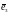 имеют координаты
имеют координаты
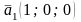 ,
,
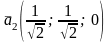 ,
,
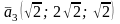 .
.
Задача
7. Плоскость
поворачивается вокруг точки
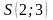 на угол
:
на угол
:
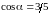 ,
,
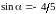 .
В какую прямую при этом преобразовании
перейдет прямая
.
В какую прямую при этом преобразовании
перейдет прямая
 :
:
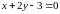 ?
?
Решение:
Поворот
плоскости на угол
вокруг некоторой точки
 аналитически описывается следующими
формулами:
аналитически описывается следующими
формулами:
 (1),
(1),
где
точка с координатами
 (старые координаты) переходит в точку
с координатами
(старые координаты) переходит в точку
с координатами
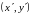 (новые координаты).
(новые координаты).
Подставив данные значения в уравнения, получим:
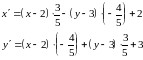
После
упрощений
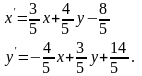 (2)
(2)
Решив
совместно систему уравнений (2) относительно
 и
и
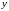 ,
полученные выражения можем подставить
в уравнение прямой
:
,
полученные выражения можем подставить
в уравнение прямой
:

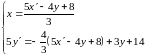
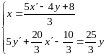
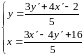
:
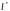 :
:
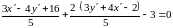
:
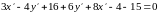
:
 .
.
Ответ: образ прямой – прямая : .
Задача
8. Написать
формулы скользящей симметрии, заданной
осью
 и вектором
и вектором
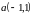 .
.
Решение:
Ось
симметрии в системе координат
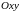 ,
проходящая через точку с координатами
,
проходящая через точку с координатами
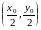 и наклоненная под углом
и наклоненная под углом
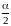 к оси
к оси
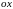 ,
имеет уравнение
,
имеет уравнение
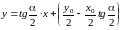 .
.
В
условии задана ось
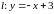 ,
значит,
,
значит,
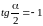 и
и
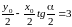 .
.
Ось
симметрии – вертикальная линия, так
как
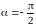 .
.
Координаты
вектора
 связаны с углом наклона оси симметрии
соотношениями:
связаны с углом наклона оси симметрии
соотношениями:
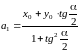 ,
,
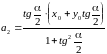 .
.
Обобщив все данные, получим следующую систему:

или, упростив,
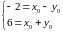
Значит,
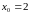 ,
,
 .
.
Скользящая симметрия, определяемая как движение II рода, аналитически описывается формулами:
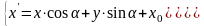
Подставляя
полученные значения (
,
,
),
находим описание скользящей симметрии
с осью
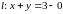 и вектором
и вектором
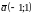 :
:
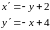
Задача
9. В
системе координат
заданы точки
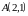 ,
,
 ,
,
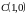 ,
,
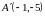 ,
,
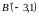 ,
,
 .
Показать, что треугольники
.
Показать, что треугольники
 и
и
 гомотетичны и написать формулы гомотетии.
гомотетичны и написать формулы гомотетии.
Решение:
Гомотетией
называется геометрическое преобразование,
отображающее каждую точку
 в такую точку
в такую точку
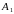 ,
что
,
что
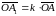 ,
где число
,
где число
 называется коэффициентом гомотетии.
При гомотетии для точек
,
называется коэффициентом гомотетии.
При гомотетии для точек
,
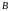 и их образов
и их образов
 ,
,
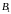 выполняется:
выполняется:
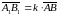 .
.
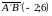 ;
; 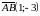
 ;
; 
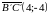 ;
; 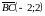 .
.
Видно,
что 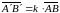

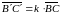 ,
где
,
где
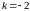 ,
значит треугольники гомотетичны.
,
значит треугольники гомотетичны.
Аналитическое
описание гомотетии с коэффициентом
и центром гомотетии
 :
:
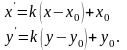
Согласно
условию, точка
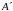 – образ точки
при указанной гомотетии, значит:
– образ точки
при указанной гомотетии, значит:

Решив
систему, находим координаты центра
гомотетии :
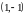 .
.
Тогда формулы гомотетии имеют вид:
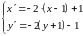 ,
или
,
или

Задача
10. Написать
формулы преобразования подобия второго
рода, при котором точки
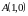 ;
;
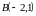 переходят соответственно в точки
переходят соответственно в точки
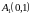 ,
,
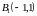 в репере
в репере
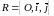 ,
определить инвариантную точку подобия.
,
определить инвариантную точку подобия.
Решение:
Длины
отрезков
 и
и
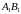 соответственно равны
соответственно равны
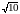 и
и
 .
.
Аналитическое описание подобия 2 рода :
 (3).
(3).
Найдем коэффициенты подобия. Если отрезок переходит в отрезок , то их длины связаны соотношением:
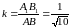
Точка
переходит в точку
,
а
– в точку
.
Подставляя данные координаты в уравнения
(3), получим систему четырех уравнений
с четырьмя неизвестными:
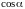 ,
,
 ,
,
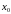 ,
,
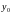 :
:

Решив систему, получим следующие значения:
 ,
,
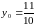 ,
,
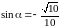 ,
,
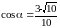 .
.
Значит,
аналитическое описание данного
преобразования будет таким:
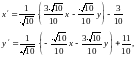
или, после упрощений,
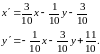
Неподвижная (инвариантная) точка – это точка, которая при каком-либо преобразовании переходит в себя. Пусть ее координаты , тогда

Решением
системы является пара
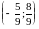 ,
,
поэтому неподвижная точка имеет координаты .
Ответ: 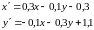
.
Задача
11. Найти
уравнения и координаты проективной
прямой, проходящей через точки
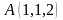 и
и
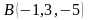 .
.
Решение:
Уравнение
проективной прямой, проходящей через
точки
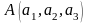 и
и
 ,
имеет вид:
,
имеет вид:

Так как прямая проходит через точки и , то уравнение прямой примет вид:
 .
.
Теперь запишем координаты данной прямой в общем виде:
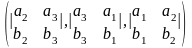 ,
таким образом
,
таким образом
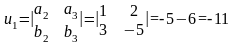
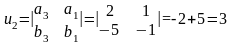

С
учетом полученных значений координат
получим общее уравнение прямой
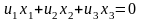 ;
;
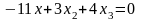 .
.
Из
равенства нулю определителя в исходном
уравнении прямой с учетом его свойств
получим соотношение
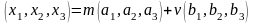 и параметрические уравнения прямой
и параметрические уравнения прямой
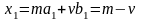
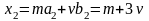
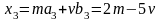 .
.
Ответ:
уравнение прямой
 ;
;
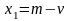 ,
,
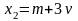 ,
,
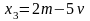 ,
,
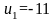 ,
,
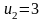 ,
,
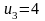 .
.
Задача
12. Выяснить,
имеют ли данные прямые
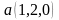 ,
,
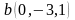 ,
,
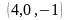 общую точку.
общую точку.
Решение:
Необходимым
и достаточным условием того, что три
прямые
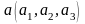 ,
,
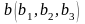 ,
,
 имеют общую точку, является равенство
имеют общую точку, является равенство
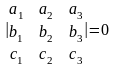 ,
таким образом
,
таким образом
 ,
,
значит,
прямые
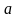 ,
,
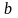 и
и
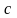 не имеют общей точки.
не имеют общей точки.
Наличие общей точки и ее координаты можно обнаружить, решив систему
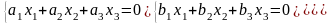
В
этом случае тройка чисел
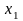 ,
,
 ,
,
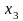 ,
удовлетворяющая уравнениям системы,
будет координатами общей точки.
,
удовлетворяющая уравнениям системы,
будет координатами общей точки.
Задача
13. На
расширенной прямой
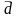 задан репер
задан репер
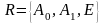 .
Построить точку
.
Построить точку
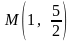 по ее координатам в данном репере.
по ее координатам в данном репере.
Решение:
Опишем ход построения точки P.
Изобразим на чертеже данную расширенную прямую .
Возьмем точку
 ,
не принадлежащую прямой
,
и пучок прямых с центром в этой точке:
,
не принадлежащую прямой
,
и пучок прямых с центром в этой точке:
 .
.На прямой
 возьмем произвольный вектор
возьмем произвольный вектор
 .
.Построим согласованную систему векторов:
 ,
используя правило параллелограмма для
сложения векторов.
,
используя правило параллелограмма для
сложения векторов.Точка М имеет координаты . Это означает, что точку М должен порождать вектор
 .
Построим его по правилу параллелограмма.
.
Построим его по правилу параллелограмма.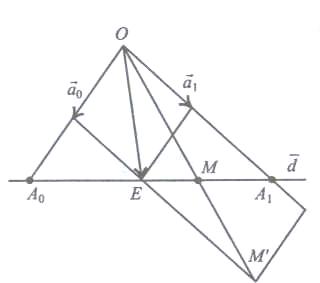 Точку
М получим как точку пересечения прямой,
которой принадлежит вектор
Точку
М получим как точку пересечения прямой,
которой принадлежит вектор
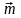 ,
и прямой
,
и прямой
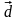 .
.
Все построения точки М показаны на рис.
Задача
14. На
расширенной плоскости
 задан репер
задан репер
 .
Построить точку
.
Построить точку
 по ее координатам в данном репере.
по ее координатам в данном репере.
Решение:
Задание
репера
означает существование координатного
треугольника
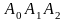 и согласованность системы векторов
и согласованность системы векторов
 ,
,
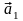 ,
,
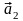 ,
,
порождающих вершины координатного
треугольника и единичную точку
,
,
порождающих вершины координатного
треугольника и единичную точку
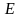 :
:

Если
на плоскости задан репер
,
то на каждой из координатных прямых
возникает свой репер:
 на прямой
на прямой
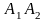 ;
;
 на прямой
на прямой
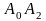 ;
;
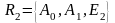 на прямой
на прямой
 .
.
Тогда ход построения:
Построить
какие-нибудь две ее проекции на
координатные оси, например
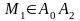 и
и
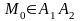 ,
тогда
,
тогда
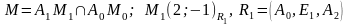 ,
где
,
где
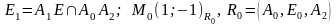 ,
где
,
где
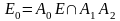 .
.
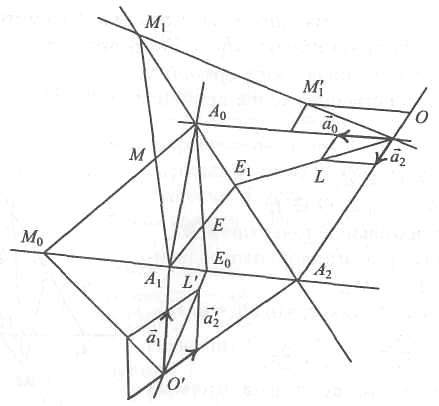
Задача
15. В
проективном репере
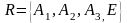 построить прямую
построить прямую
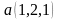 .
.
Решение:
Запишем
уравнение прямой
:
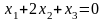 .
Для того, чтобы построить прямую
,
достаточно построить две ее точки, а
затем через них провести прямую. Точки
.
Для того, чтобы построить прямую
,
достаточно построить две ее точки, а
затем через них провести прямую. Точки
 и
и
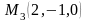 лежат на прямой
.
Их построение аналогично построениям
в задаче 5.
лежат на прямой
.
Их построение аналогично построениям
в задаче 5.
возьмем точку
 ,
не лежащую на
,
не лежащую на
 ,
и в аффинной системе с началом
и единичной точкой
,
и в аффинной системе с началом
и единичной точкой
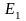 построим
построим
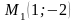 .
. .
.возьмем точку
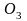 ,
не лежащую на
,
и в аффинной системе с началом
и единичной точкой
,
не лежащую на
,
и в аффинной системе с началом
и единичной точкой
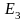 построим
построим
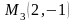 .
. .
.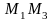 – искомая
прямая
.
– искомая
прямая
.

Задача
16. Вычислить
сложное отношение четырех точек по их
проективным координатам на плоскости
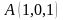 ,
,
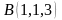 ,
,
 ,
,
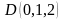 .
.
Решение:
Сложное
отношение четырех точек равно сложному
отношению их проекций. Рассмотрим
проективный репер
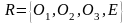 и возьмем проекции
и возьмем проекции
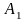 ,
,
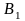 ,
,
 ,
,
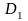 точек
точек
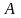 ,
,
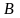 ,
,
 ,
,
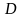 из центра
на координатную прямую
из центра
на координатную прямую
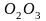 .
Их координаты в проективном репере
.
Их координаты в проективном репере
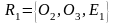 будут
будут
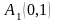 ,
,
 ,
,
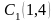 ,
,
 .
Сложное отношение точек
.
Сложное отношение точек
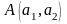 ,
,
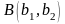 ,
,
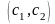 ,
,
 это число, вычисляемое по формуле
это число, вычисляемое по формуле
 .
.
Значит,
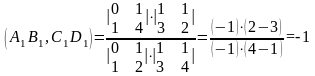 .
.
Сложное
отношение точек
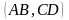 равно -1, что означает, что четыре точки
находятся в гармоническом отношении.
равно -1, что означает, что четыре точки
находятся в гармоническом отношении.
Ответ:
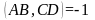 .
.
Задача 17. Найти внутренность, дополнение, границу и замыкание
а)
отрезка
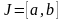 на числовой прямой
на числовой прямой
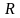 ;
;
б)
замкнутого шара
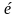 :
:
 в евклидовом пространстве
.
в евклидовом пространстве
.
Решение:
а)
Внутренность множества состоит из
точек, имеющих окрестности, целиком
лежащие в этом множестве. У отрезка
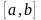 существуют две точки, окрестности
которых состоят не только из точек,
лежащих в нем, – это точки
и
.
существуют две точки, окрестности
которых состоят не только из точек,
лежащих в нем, – это точки
и
.
Значит,
внутренностью отрезка
будет интервал
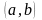 .
На символах можно записать так:
.
На символах можно записать так:
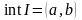 ,
или
,
или
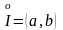 .
.
Дополнение состоит из точек, не принадлежащих внутренности, то есть
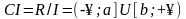 .
.
Граница
некоторого множества состоит из граничных
точек, то есть таких, любые окрестности
которых содержат точки как из множества,
так и из его дополнения. Граница множества
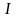 состоит из точек
,
:
состоит из точек
,
:
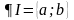 .
.
Замыкание множества можно получить, объединив внутренность множества и его границу:
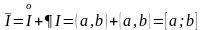 ,
,
то есть в данном случае замыкание отрезка есть сам отрезок.
б) В евклидовом пространстве определения внутренности, дополнения, границы и замыкания будут такими же. Поэтому
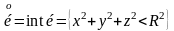 .
.
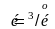
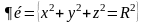
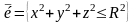 .
.
Задача 18. Найти эйлерову характеристику квадрата.
Решение:
Эйлерова
характеристика – это число
,
вычисляемое по формуле:
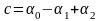 ,
где
,
где
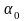 – число
вершин (точек);
– число
вершин (точек);
 – число
сторон (ребер);
– число
сторон (ребер);
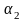 – число
клеток (граней).
– число
клеток (граней).
Так
как для квадрата
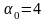 ,
,
 ,
,
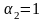 ,
то
,
то

Ответ:
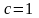 .
.
Задача 19. Доказать, что:
а)
полуокружность
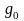 с концами
с концами
 ,
,
 гомеоморфна отрезку
гомеоморфна отрезку
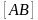 ;
;
б) сфера с выколотой точкой (т. е. без полюса) гомеоморфна плоскости.
Решение:
Для того, чтобы доказать гомеоморфность двух фигур (точнее, двух топологических пространств), надо установить взаимно-однозначное непрерывное отображение любой из них на другую, для которого обратное отображение тоже непрерывно. Если каждый элемент из какого-то множества, например из , имеет один и только один прообраз во множестве , то отображение является взаимно-однозначным. Если же близкие элементы множества переходят в близкие элементы множества , то отображение будет непрерывным. Используем эту теорию при решении задачи.
а) Расположим отрезок на касательной к полуокружности таким образом, что ортогональные проекции точек , есть точки , (рис. 4).
Зададим
следующее отображение
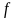 :
каждой точке
:
каждой точке
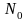 множества
поставим в соответствие ортогональную
проекцию этой точки на отрезок
.
Очевидно, что заданное отображение
будет удовлетворять всем признакам
определения гомеоморфизма, то есть
отображение
– гомеоморфизм, а фигуры
и
гомеоморфны.
множества
поставим в соответствие ортогональную
проекцию этой точки на отрезок
.
Очевидно, что заданное отображение
будет удовлетворять всем признакам
определения гомеоморфизма, то есть
отображение
– гомеоморфизм, а фигуры
и
гомеоморфны.
б)
Расположение сферы и плоскости
показано на рис. 5 (плоскость
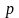 касается сферы
касается сферы
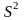 в точке
,
диаметрально противоположной точке
).
в точке
,
диаметрально противоположной точке
).
Отображение
установим следующим образом: любой
точке
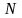 сферы
поставим в соответствие точку
сферы
поставим в соответствие точку
 плоскости
:
плоскости
:
 .
Аналогично предыдущему примеру
отображение
будет гомеоморфизмом, т. е. сфера без
полюса и плоскость гомеоморфны.
.
Аналогично предыдущему примеру
отображение
будет гомеоморфизмом, т. е. сфера без
полюса и плоскость гомеоморфны.
Замечание:
Для доказательства негомеоморфности двух пространств (множеств) обычно определяется различающий топологический инвариант (компактность, связность, отделимость, мощность и т. д.), которым одно из пространств (множеств) обладает, а другое нет. Например, отрезок числовой оси компактен (т. к. ограничен и замкнут), а интервал – нет. Поэтому они негомеоморфны.
Любая наука занимается изучением определенных моделей реального мира. Описывая что-либо словами, мы формулируем модель какого-то реального события или объекта. Но при этом модель вряд ли будет точной копией объекта. В модели всегда присутствует неопределенность, которую необходимо учитывать в дальнейших рассуждениях и исследованиях. Существуют разные типы неопределенностей. Во-первых, это физическая неопределенность. Например, хоть мы и имеем на руках рулетку всегда сложно измерить расстояние с точностью до, например, микрона. Или как узнать вероятность того, что первый встречный человек будет из другого города? Физическая неопределенность может быть следствием неточности (проблемы такого рода позволяет разрешить теория измерений) или случайности (это объект изучения теории вероятностей). Второй вид неопределенности – это лингвистическая неопределенность. Она может возникать в результате неопределенности смысла фраз, этим вопросом занимается теория формальных грамматик. Примером такого рода неопределенности может служить известная фраза «Казнить нельзя помиловать». Либо причиной лингвистической неопределенности может быть неопределенность значений слов. Как точно описать значение понятий «человек среднего роста», «высокий уровень безопасности» и пр.? Этими вопросами занимается теория нечетких множеств. Способность человека принимать правильные решения в обстановке неполной и нечеткой информации является наиболее поразительным свойством человеческого интеллекта. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.
Значительное продвижение в этом направлении сделано в 1965 г. профессором Калифорнийского университета Лотфи А. Заде. Что же предложил Заде? Во-первых, он расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.
Введя затем понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Л.Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.
Дальнейшие работы профессора Л.Заде и его последователей заложили прочный фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.
В последние 5-7 лет началось использование новых методов и моделей в промышленности. И хотя первые применения нечетких систем управления состоялись в Европе, наиболее интенсивно внедряются такие системы в Японии. Математическая теория нечетких множеств, предложенная Л.Заде, позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров. Спектр приложений их широк: от управления процессом отправления и остановки поезда метрополитена, управления грузовыми лифтами и доменной печью до стиральных машин, пылесосов и СВЧ-печей. Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы.
Вспомним, что понятие множества является одним из основных понятий математики. Оно вводится аксиоматически и не может быть определено через какие-то элементарные понятия. Существует описательное объяснение, согласно которому множество –это совокупность, объединение некоторых элементов произвольной природы по какому-то признаку. Этот признак содержится в названии множества. Например, множество целых чисел, множество студентов института и т.д .
Если E - универсальное множество, x - элемент E, а R - некоторое свойство, то обычное (четкое) множество A универсального множества E, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар A = {A (х)/х}, где A(х) - характеристическая функция, принимающая значение 1, если x удовлетворяет свойству R, и 0 - в противном случае.
Например, буквы латинского алфавита X, Y, Z принадлежат множеству {B, M, Z, F,Y, X}, а буквы R,K-не принадлежат. Тогда данное множество является четким и верна запись {X/1, Y/1, Z/1} и {R/0, K/0}.
Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "да-нет" относительно свойства R. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар A = {A(х)/х}, где A(х) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве M (например, M = [0,1], но эта область может быть и такой [-1, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называют множеством принадлежностей. Если M = {0,1}, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.
Нечеткие числа - нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности A(x)[0,1], где x - действительное число, т.е. xR.
Нечеткое число показывает степень соответствия объекта данному нечеткому множеству. Причем:
а) существует такое значение носителя, в котором функция принадлежности равна 1, б) при отступлении от своего максимума влево или вправо функция принадлежности убывает.
Нечеткое
число А нормально,
если
![]() A(x)=1,
выпуклое,
если для любых xyz выполняется
A(x)=1,
выпуклое,
если для любых xyz выполняется
A(x)A(y)A(z).
Множество - уровня нечеткого числа А определяется как
А = {x/ A(x)}.
Подмножество SAR называется носителем нечеткого числа А, если
S = {x/A(x)>0}.
Нечеткое число А унимодально, если условие A(x) = 1 справедливо только для одной точки действительной оси.
Выпуклое
нечеткое число А называется нечетким
нулем,
если A(0)
=
![]() (A(x)).
(A(x)).
Нечеткое число А положительно, если xSA, x>0 и отрицательно, если xSA, x<0.
Итак, нечеткое множество- это множество значений носителя, такое, что каждому значению носителя сопоставлена степень принадлежности этого значения данному множеству.
Выделяют трапециевидные и треугольные нечеткие числа, функции принадлежности которых имеют соответственно вид:
Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).
Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):
Вычислениями над нечеткими числами занимается отдельный раздел теории нечетких множеств - мягкие вычисления (нечеткая арифметика). Эти операции вводятся через операции над функциями принадлежности. Как и в арифметике, используют операции «сложения», «вычитания», «умножения» и пр.
Примеры записи нечеткого множества
Пусть E = {x1, x2, x3, x4, x5 }, M = [0,1]; A - нечеткое множество, для которого
A(x1)=0,3; A(x2)=0; A(x3)=1; A(x4)=0,5; A(x5)=0,9.
Тогда A можно представить в виде:
A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } или
A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5, или
-
A =
x1
x2
x3
x4
x5
0,3
0
1
0,5
0,9
.
Замечание. Здесь знак "+" не является обозначением операции сложения, а имеет смысл объединения.
Пусть Х=(1,2.3.4,5,6,7,8,9.10). Тогда нечеткое множество «большие числа» может быть представлено следующим образом: А= «большие числа»=0,2/6+0,5/7+0,8/8+1/9+1/10. Это следует понимать следующим образом: 9 и 10 с абсолютной уверенностью можно отнести к «большим числам», 8 есть большое число со степенью 0,8, 1,2,3,4,5 абсолютно не являются большими числами.
Функцию принадлежности можно изображать графически. Например, график функции принадлежности «Оптимальный возраст работника».
Видно, что возраст от 20 до 30 оценивается экспертами как бесспорно оптимальный, а от 60 и выше- как неоптимальный. В диапазоне от 35 до 60 эксперты проявляют неуверенность в своей классификации, структура которой передается графиком функции принадлежности.
