Вопрос 9. Прямая и плоскость в пространсте., их уравнения. Взаимное расположение прямых и плоскостей.

Одной из простейших геометрических фигур является прямая. Алгебраическое уравнение прямой также имеет простой вид, который можно легко получить, пользуясь векторным методом.

Положение прямой на плоскости относительно выбранной системы координат вполне определяется какой-либо точкой М₀ (х_0, у₀) этой прямой и ненулевым вектором n, перпендикулярным к прямой. Вектор n называется вектором нормали. На рисунке изображена прямая, указанный вектор и две точки, М и М₀, принадлежащие прямой. Как следует из предыдущей лекции, скалярное произведение векторов n и М₀М равно нулю, так как они взаимно перпендикулярны. Следовательно, обозначив через А и В координаты вектора нормали, получим координатное представление скалярного произведения векторов n и М₀М , то есть уравнение А(х–х₀)+В(у – у₀) = 0. Раскрыв скобки в этом уравнении и обозначив число (-Ах₀–Ву₀) буквой С, получим А х + В у + С = 0 Это уравнение называется общим уравнением прямой на плоскости.

Преобразовав данное уравнение, можно получить и другие способы задания прямой. Так, например, перенесем С в правую часть и разделим обе части получившегося выражения на (-С). Получим . Обозначив выражения, стоящие в знаменателе, соответственно за а и b, получим уравнение прямой в отрезках, где a и b – отрезки, отсекаемые прямой на осях OX и OY соответственно:

С другой стороны, выразим в общем уравнении прямой переменную у, перенеся все лишние переменные в правую часть и произведя необходимую процедуру деления: , получим известное из алгебры уравнение прямой через угловой коэффициент.

Любую прямую также можно задать с помощью точки, принадлежащей прямой и вектора, параллельного ей (направляющий вектор). Тогда, если М₀ (х_0, у₀)-точка прямой, М (х,у) – любая другая точка этой прямой, то вектор М₀М и направляющий вектор прямой (пусть, например, это вектор р(р ₁ , р₂ ) ) будут коллинеарны. А мы знаем, что в этом случае их координаты пропорциональны, то есть можно записать подставим координаты векторов: Используя свойства произведения вектора на число и равенства векторов, получаем два условия:

Запись называется параметрическими уравнениями прямой линии.

Как известно из школьного курса геометрии, любую прямую можно задать при помощи двух точек. Пусть это точки М₁ (х_1, у₁) и М₂ (х_2, у₂). Точка М(х,y) – произвольная точка этой прямой. Тогда вектора М₁М₂ и М₁М будут коллинеарны. Можно записать следующую цепочку равенств:

Приравняв обе дроби, получим уравнение прямой, проходящей через две заданные точки.

Если две прямые заданы уравнениями общего вида А₁ х + В₁ у + С₁ = 0 и А₂ х + В₂ у + С₂ = 0, то можно установить их взаимное расположение. Так, если коэффициенты при переменных х и y пропорциональны, то прямые параллельные, если пропорциональны все три коэффициента, включая и свободный член, то прямые совпадают. Во всех остальных случаях прямые пересекаются. В этих случаях речь может идти об угле пересечения двух прямых. При пересечении прямые образуют четыре попарно равных угла. Наименьший из этих углов будем называть углом между прямыми.

Так как каждая из прямых однозначно определяется направляющим вектором, то угол между прямыми будет совпадать с углом между этими векторами. Для первой прямой направляющий вектор имеет координаты n₁(-В₁, А₁ ), для второй n₂ (-В₂ ,А₂ ). А угол между векторами можно найти, пользуясь скалярным произведением, то есть

Расстояние d от точки М₀ (х_0, у₀) до прямой, заданной общим уравнением А х + В у + С = 0, вычисляется по формуле

Пространственные варианты представленных формул будут иметь похожий вид, доказательство формул аналогично рассмотренному выше.

Н апример, прямая, заданная заданной точкой M ₀(x₀, y₀, z₀) и направляющим вектором р (р₁, р₂, р₃) : определяется уравнением:

, которое называется каноническим.

Прямая, заданная двумя точками М₁(x₁, y₁, z₁), M₂(x₂ y₂, z₂) имеет уравнение:

И, наконец, параметрические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) и имеющую направляющий вектор р (р₁, р₂, р₃) –уравнениями

В пространстве, кроме прямой, аналитическая геометрия изучает еще один объект – плоскость. Перечислим основные способы задания плоскости. Плоскость может быть задана тремя точками М₁(x₁, y₁, z₁), M₂(x₂ y₂, z₂), M₃ (x₃, y₃, z₃). В этом случае три вектора М₁М, М₂ М₁ и M₃М₁ будут коллинеарными. А это означает, что они лежат в одной плоскости и объем параллелепипеда, построенного на этих векторах, будет равен нулю. Соответственно, будет равно нулю и их смешанное произведение, то есть Эта формула носит название уравнения плоскости, проходящей через три заданные точки.

Аналогично, можно получить уравнение плоскости, заданной точкой М₀ (х₀, у₀, z₀) и двумя векторами, определяющими саму плоскость а (а₁, а₂, а₃), b (b_1, b₂, b₃):

Также при этом задании можно получить и параметрические уравнения плоскости:

Если дана точка M ₀(x₀, y₀, z₀) и вектор, который перпендикулярен к плоскости (вектор нормали плоскости) n(A, B, C), то при составлении уравнения плоскости можно воспользоваться представлением скалярного произведения через координаты и в результате получить уравнение A(х – х₀) + B(у – у₀) + C(z – z₀) = 0. И конечно же, как и в случае прямой, определено общее уравнение плоскости, имеющее вид Ах + Ву + Сz +D = 0. И уравнение плоскости в отрезках: где a, b, c – отрезки, отсекаемые плоскостью на осях координат.

Используя аналитическое выражение прямой и плоскости, воз­можно исследовать различные случаи взаимного расположения как двух прямых, так и прямой и плоскости, рассматривая в случае их пе­ресечения углы.

Приведем формулы, используемые при решении задач на прямую и плоскость.

1. Расстояние от точки М(х₀,y₀,z₀) до плоскости  Ax+By+Cz+D=0

2. Угол между плоскостями А₁x+B₁y+C₁z+D₁=0 и

А₂х+B₂ y+C₂z+D₂=0:

 =

3 . Угол между двумя прямыми с направляющими векторами p(p_1,p_2,p₃) и q(q₁,q₂,q₃):

=

4. Угол между прямой с направляющим вектором p(p₁, p₂, p₃) и плоскостью Аx+By+Cz+D=0:

5. Расстояние от точки М до прямой, заданной точкой М₀ и направляющим вектором p :

6. Расстояние между двумя скрещивающимися прямыми d₁ (заданной точкой М₁ и вектором p₁) и d₂ (заданной точкой М₂ и вектором p₂):

7. Взаимное расположение плоскостей и :

а) параллельны, если При этом расстояние между параллельными прямыми вычисляется по формуле , причем коэффициенты при переменных должны быть равны. Для этого одно уравнение необходимо разделить на какое-то число или умножить.

б) совпадают, если

в) пересекаются по прямой, если ни одно из вышеприведенных равенств не выполняется.

В этом случае есть смысл говорить об угле между пересекающимися плоскостями, который находится по формуле и

Взаимное расположение прямых

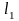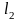4. Взаимное расположение прямых и , заданных точками , и направляющими векторами соответственно определяется по следующим условиям:

а) и параллельны, если направляющие векторы коллинеарны, то есть 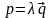, но или

б) и совпадают, если направляющие векторы коллинеарны, то есть ,а также и

в) и пересекаются, если 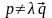, , или смешанное произведение из трех определяющих векторов равно нулю:

Угол между двумя прямыми определяется из формулы

г) и скрещиваются, если смешанное произведение трех определяющих векторов отлично от нуля:

Расстояние между двумя скрещивающимися прямыми и в этом случае определяется по формуле:

5. Расстояние от точки М до прямой, заданной точкой М₀ и направляющим вектором p :