
- •Вопрос 8. Линии второго порядка, их канонические уравнения, фокусы, директрисы., асимптоты.
- •Вопрос 9. Прямая и плоскость в пространсте., их уравнения. Взаимное расположение прямых и плоскостей.
- •Взаимное расположение прямой и плоскости
- •Вопрос 10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •Проективная прямая и ее уравнение.
- •Линии второго порядка на проективной плоскости
- •Вопрос 11. Операции над векторами
- •2) C перпендикулярен к плоскости векторов а и b, если они приведены к общему началу.
- •Обозначается ab или a, b .
- •Вопрос 25. Задача потребительского выбора.
- •Вопрос 26. Понятие эластичности, геометрический смысл. Свойства эластичности.
- •Вопрос 27. Производственная функция. Закон убывающей эффективности.
- •Вопрос 29. Задача линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •Алгоритм решения задач
- •Вопрос 30. Нелинейное программирование
- •Вторая часть. Информатика.
- •Вопрос 25. Теория вычислительных погрешностей.
- •2) Если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности:
- •Вопрос 26. Нечеткие вычисления.
- •Примеры нечетких множеств
- •Нечеткие отношения
- •3. Правила записи приближенных чисел
- •Погрешность метода определяется третьей причиной, причем появление этой погрешности практически неизбежно при любых вычислениях.
- •2) Если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности:
- •3. Правила записи приближенных чисел
- •Примеры решения задач
- •Основные характеристики нечетких множеств
- •Примеры нечетких множеств
- •О методах построения функций принадлежности нечетких множеств
- •Свойства операций и .
- •Нечеткие отношения
- •Нечеткая и лингвистическая переменные
Линии второго порядка на проективной плоскости
Множество всех точек проективной плоскости, координаты которых удовлетворяют в некотором репере R уравнению второй степени:
a11x12+a22x22+a33x32+2a12x1x2+2a13x1x3+2a23x2x3=0, называется линией (ЛВП) или кривой второго порядка, причем коэффициенты aij≠0 одновременно.
Понятие ЛВП не зависит от выбора репера.
Ранг квадратичной формы ∑aijxixj=0 называется рангом ЛВП.
Линия называется невырожденной, если её ранг равен трем и вырожденная, если ранг меньше трех.
Лемма: Любая прямая пересекает невырожденную ЛВП не более чем в двух точках.
Проективная классификация ЛВП.
Рассмотрим квадратичную форму. В векторном пространстве известно, что всегда существует базис, в котором квадратичная форма имеет нормальный вид: е1х12+е2х22+е3х32=0, где е1, е2, е3=±1 или 0.
Поэтому можно выделить следующие виды ЛВП на проективной плоскости:
Если r = 3 х12+х22+х32=0 – такая линия называется нулевой
х12+х22-х32=0 – овальная ЛВП
Если r = 2 х12+х22=0 – пара мнимых пересекающихся прямых
х12-х22=0 – пара действительных пересекающихся прямых
Если r = 1 х12=0 – пара совпавшихся прямых.
Вопрос 11. Операции над векторами
Для раскрытия первого вопроса достаточно дать определения скалярного, векторного и смешанного произведения векторов, перечислить их основные свойства (которые в ряде учебных пособий представлены в виде теории), и представить доказательство некоторых свойств. Необходимо знать специфические свойства каждого из произведений. Например, некоторые свойства скалярного произведения векторов совпадают с соответствующими свойствами произведения чисел: а*в= в* а, а*(в+с}=а*в+а*с. Но скалярное произведение обладает и особыми свойствами, которыми не обладает произведение чисел. Вот некоторые из них: а) Скалярное произведение двух векторов есть число, множественное. Объект не той природы, что сомножители, а другой, б) Для чисел, если х-y=о, то это означает, что одно из чисел равно нулю. Аналогичного свойства для векторов нет. в) Если о, то числовое уравнение ах= имеет единственное решение (х=/2).Но уравнение для скалярного произведения в-в =х= не имеет смысла (а для векторного произведения вопроса не имеет). Затем целесообразно перечислить приложение скалярного, векторного и смешанного произведения векторов к решению задач. Например, векторное произведение векторов находит свое, применение при нахождении площади треугольника, смешанное произведение - объема тетраэдра и привести примеры задач.
При ответе на этот вопрос от студента требуется знание основных понятий , включая понятия вектора , базиса векторов , линейно зависимые и линейно независимые векторы , линейной комбинации векторов. Необходимо знать, как выражается различное произведение векторов через координаты вектора.
Теорема
1: Скалярное произведение векторов
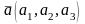 и
и
 ,
заданные в ортонормированном базисе,
выражается формулой:
,
заданные в ортонормированном базисе,
выражается формулой:
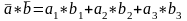 .
.
Теорема
2: Если векторы
 в ортонормированном базисе имеют
координаты
в ортонормированном базисе имеют
координаты
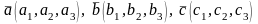 ,
то
,
то
 ,
где
,
где
 =
1, если базис правый, и
=
-1, если базис левый
=
1, если базис правый, и
=
-1, если базис левый
Теорема
3: Если векторы
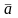 и
и
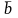 в ортонормированном правом базисе имеют
координаты
и
,
то вектор [
в ортонормированном правом базисе имеют
координаты
и
,
то вектор [ ]имеет
координаты:
]имеет
координаты:
[
]
 Докажем это.
Докажем это.
Пусть координаты вектора [ ] (x,y,z).
Тогда
[
]=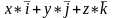
[
]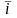 =
=
[
]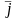 =
=
[
] =
=
С
учетом предыдущей теоремы и условий
ортонормированности базиса( ),
получили
),
получили
X=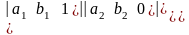 ;
Y=
;
Y=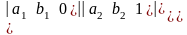 ;
Z=
;
Z= что и требовалось доказать.
что и требовалось доказать.
Основные определения:
Направленный
отрезок (упорядоченную пару точек)
называют вектором.
Обозначают АВ
или
 Здесь
A
– начало вектора, B
– конец вектора. Расстояние между
началом и концом вектора называют
его длиной
(или модулем, или абсолютной величиной).
Обозначают |АВ
| или |
Здесь
A
– начало вектора, B
– конец вектора. Расстояние между
началом и концом вектора называют
его длиной
(или модулем, или абсолютной величиной).
Обозначают |АВ
| или |
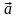 |. Если точки А и В совпадают, то вектор
называют нулевым и обозначают знаком
|. Если точки А и В совпадают, то вектор
называют нулевым и обозначают знаком
 Его модуль равен нулю.
Его модуль равен нулю.
Векторы называются коллинеарными, если они лежат на параллельных прямых (или на одной прямой). Ненулевые коллинеарные векторы либо имеют одно и тоже направление и называются в этом случае сонаправленными, или одинаково направленными, либо имеют противоположные направления и называются противоположно направленными. Векторы называются компланарными, если они лежат в одной плоскости или параллельных плоскостях. Нулевой вектор коллинеарен любому вектору. Два ненулевых вектора называются равными, если они одинаково направлены и имеют одну и ту же длину. От каждой точки можно отложить единственный вектор, равный данному.
Над векторами можно выполнять следующие операции:
1) Сложение векторов.
Суммой а + b двух векторов a и b называется вектор, который идет из начала вектора a в конец вектора b, при условии, что вектор b отложен от конца вектора a. Это построение называется правилом треугольника. Сумма векторов a + b не зависит от выбора начала вектора a.
Если векторы а и b приведены к общему началу и на них построен параллелограмм, то сумма а + b есть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала векторов а и b. Это построение называется правилом параллелограмма.
2) Вычитание векторов.
Разностью векторов а и b называется такой вектор x, что b+x=a. Если векторы а и b имеют общее начало, то их разность есть вектор, идущий из конца вектора b в конец вектора a.
Изобразим перечисленные правила на чертеже.

3)Умножение вектора на число.
Произведением ненулевого вектора a на действительное число 0 называется вектор b, обозначаемый b= а, и определенный следующими условиями
b = а
Вектор b коллинеарен вектору a.
Векторы b и a направлены одинаково, если 0 и противоположно, если 0. Если a=
 или =0,
то полагают a
=
.
или =0,
то полагают a
=
.
Система векторов а1, а2, …,аm называется линейно зависимой, если существуют такие действительные числа с1, с2, …,сm, одновременно не равные нулю, что имеет место равенство c1a1+с2a2+..сmam =0. В противном случае эта система векторов называется линейно независимой.
Имеют место следующие теоремы:
Т1. Любые два коллинеарных вектора линейно зависимы и наоборот, два неколлинеарных вектора линейно независимы.
Т2. Три компланарных вектора линейно зависимы и наоборот, три некомпланарных вектора линейно независимы.
Т3. Каждые четыре вектора в пространстве линейно зависимы.
Базисом на плоскости является любая упорядоченная пара неколлинеарных векторов этой плоскости. Базисом в пространстве является любая упорядоченная тройка некомпланарных векторов.
Рассмотрим систему векторов a1, a2,….,am и зададим m действительных чисел c1, с2, …,сm. Вектор b= c1a1+с2a2+…+сmam называется линейной комбинацией данных векторов a1, a2,…,am.
Т4. Пусть на плоскости выбран базис е1, е2. Тогда любой вектор а этой плоскости можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.
Т5. Пусть в пространстве выбран базис е1, е2, е3 .Тогда любой вектор а пространства можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.
Если е1, е2, е3 – базис и вектор а = 1 е1 + 2 е2 + 3е3, то числа 1, 2 , 3 называются координатами вектора а в данном базисе. Записывается а (1, 2 ,3). Равные векторы имеют равные координаты.
Для векторов, заданных своими координатами, имеют место следующие свойства:
1) При умножении вектора а = 1е1+2 е2+3е3 на число его координаты умножаются на это число: а =(1)е1+(2) е2+(3)е3.
2) При сложении (вычитании) векторов а = 1 е1 + 2 е2 +3е3 и b = 1 е1 + 2 е2 +3е3 складываются (вычитаются) их соответствующие координаты: а b = (1 1 ) е1 + (2 2 ) е2 + (3 3 ) е3
Углом между двумя ненулевыми векторами а и b, где a=ОА, b=OB называется меньший угол АОВ между этими векторами.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин векторов-сомножителей на косинус угла между ними. Скалярное произведение обозначается (а,b).
По определению, (а , b) = a b cos , где - угол между векторами а и b. Если хотя бы один из векторов нулевой, то их скалярное произведение считают равным нулю.
Свойства скалярного произведения:
1. (а , b) = (b , a) для любых а и b
2. (а, a) = а 2 = a 2 для любого a
3. Если a , b , / 2, то (а , b) = 0. Если a , b , (а ,b)=0, то a b
4. (а , b) = (а , b) = (а , b) для любых а и b.
5. (а, b + c) = ( a , b) + ( а , c ) для любых а , b,с
Пусть в прямоугольной системе координат в пространстве векторы а и b заданы своими координатами: а (X1, Y1,Z1), b (X2, Y2 ,Z2). Тогда (а , b) = X1X2 + Y1Y2 + Z1Z2.
Обозначим через , , углы, которые составляет вектор а с осями координат. Косинусы этих углов называются направляющими косинусами вектора а. При этом справедливы следующие соотношения: X = а cos, Y = а cos , Z = а cos, где X, Y, Z – координаты вектора а.
Упорядоченная тройка ненулевых векторов а1, а2, а3 – с общим началом называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден в направлении, противоположном направлению движения часовой стрелки. В противном случае тройка называется левой.
Векторным произведением ненулевого вектора а на ненулевой вектор b называется вектор с, определенный следующими условиями:
1) c = a b sin ( - угол между векторами а и b )
