Взаимное расположение прямой и плоскости

Пусть прямая задана точкой и направляющим вектором , а плоскость – уравнением общего вида Ах + Ву + Сz +D = 0. Возможны следующие случаи их взаимного расположения:

а) Прямая и плоскость параллельны, если , а

б) Прямая принадлежит плоскости, если и

в) Прямая и плоскость пересекаются, если

В этом случае угол между прямой и плоскостью равен .

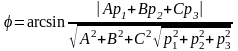Вопрос 10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.

(Ответ на удовлетворительно – без доказательств)

Проективная геометрия является одним из самых красивых разделов геометрии. Она резко отличается от евклидовой геометрии, где все необходимо строго доказывать, причем, некоторые доказательства весьма сложны, в ней не используются понятия параллельности, перпендикулярности и равенства отрезков и углов, и предполагается, что любые две прямые на плоскости имеют общую точку. В проективной геометрии ненужная информация отбрасывается, и в результате доказательство проходит просто и легко.

Как и все другие геометрии, проективная строго задается системой аксиом. В ней фигурируют два типа объектов, называемых «точками» и «прямыми». Между этими объектами есть некоторые отношения, схожие с точками и прямыми евклидовой плоскости, и для них выполняется ряд свойств, отличающихся от присущих евклидовым.

Возникновение проективной геометрии связано с именем известного французского математика Понселе. Он выделил как объект её изучения особые свойства геометрических фигур, которые были названы проективными. Эти свойства связаны с понятием центрального проектирования.

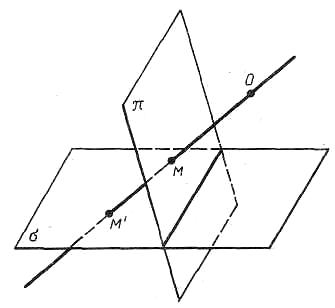Рассмотрим в Евклидовом пространстве Е₃ 2 плоскости π и σ, точку О не лежащую в этих плоскостях. Пусть М – произвольная точка, принадлежащая π. Точка М´ пересечения прямой ОМ с плоскостью σ называется проекцией точки М на плоскость σ из центра О. Точке М, принадлежащей π, поставим в соответствии её проекцию М^’ на плоскость σ из центра О.

Таким образом установленное соответствие между точками плоскостей π и σ называется центральным проектированием плоскости π на плоскость σ из центра О. Аналогично определяется и проекция фигуры.

При центральном проектировании многие свойства фигуры искажаются: меняется длина отрезка, величины углов, параллельные прямые проектируются в пересекающиеся прямые, проектируя параллелограмм можно получить произвольный четырёхугольник. Более того, проектируя отрезок, можно получить луч.

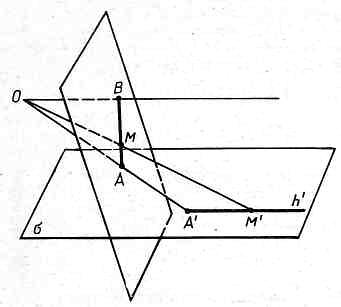
Но есть и ряд свойств, которые сохраняются при любом центральном проектировании. Эти свойства Понселе и назвал проективными. Такими свойствам является, например, свойство точек лежать на одной прямой или на одной ЛВП. Однако уже свойство точки лежать между двумя другими не является проективным.

Свойства, связанные с длинами отрезков и величин углов, также не являются проективными.

Значительное место в проективной геометрии занимает введение так называемых несобственных (или бесконечно удаленных) геометрических элементов. Введение этих элементов – заслуга другого математика, француза Жерара Дезарга. Пользуясь перспективой как общим методом исследования, Дезарг пришел к необходимости рассматривать так называемые бесконечно удаленные элементы пространства. Он считал, что все параллельные прямые пересекаются в точке, которая является таким бесконечно удаленным элементом. Этим шагом Дезарг положил начало проективному представлению пространства (полное проективное пространство) и сделал возможным изучение проективных преобразований.

Следуя за Дезаргом, дополним пространство Е₃ новыми точками, а именно: ко всем обычным точкам каждой прямой мысленно добавим ещё одну, несобственную точку. Будем считать, что две параллельные прямые имеют одну и ту же несобственную точку, а непараллельные прямые – различные. Обычные точки будем называть собственными. Прямую, дополненную несобственной точкой, назовём расширенной. Каждая плоскость имеет бесконечное множество параллельных прямых, следовательно и несобственных точек. Пусть все несобственные точки плоскости образуют несобственные прямые, а все несобственные точки пространства - несобственную плоскость. Плоскость, дополненную расширенной прямой, будем называть расширенной плоскостью. Вот и построена нами новая геометрия, которая занимает не менее важное место, чем евклидова.

Свойства, не меняющиеся при преобразованиях, и называются проективными. Именно ими и занимается проективная геометрия, остальные, изменяющиеся свойства, она игнорирует. Все теоремы проективной геометрии также касаются только проективных свойств, в них даже и не говорится ни об углах, ни о длинах.

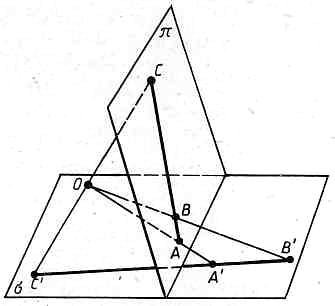
Сформулируем теорему Дезарга. Пусть на плоскости заданы точки А, В, С и точка О, через которую проходят прямые ОА, ОВ, ОС. На каждой из этих прямых выберем по одной произвольной точке – А₁, В₁, С₁. Точки пересечения прямых АВ с А₁В₁, АС с А₁С₁ и ВС с В₁С₁ лежат на одной прямой.

Из простейших фигур евклидовой геометрии можно вспомнить треугольники, четырехугольники, окружности. Есть ли похожие понятия в проективной геометрии? Ответ – положительный.

Начнем с аналога треугольника. Он называется трехвершинником. Трехвершинником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех прямых, соединяющих попарно эти точки. Указанные точки называются вершинами, а прямые — сторонами трехвершинника. Трехвершинник с вершинами А, В, С обозначается так: АВС.

На проективной плоскости рассмотрим два трехвершинника AВС и А'В'С', вершины каждого из которых заданы в том порядке, в котором они записаны. Вершины А и А',В и В', С и С' будем называть соответственными, также будем называть соответствен­ными стороны АВ и А'В', ВС и В'С', СА и СА'. Теперь рассмотренную выше теорему Дезарга можно сформулировать более точно, поскольку в ней идет речь именно о трехвершинниках.

Е

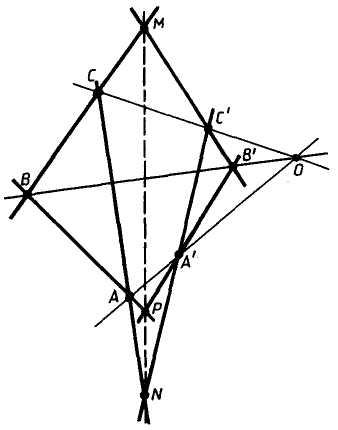
Рис. 2

сли прямые, проходящие че­рез соответственные вершины двух трехвершинников, проходят через одну точку, то соответственные стороны этих трехвершинников пе­ресекаются в точках, лежащих на одной прямой.

Другая фигура проективной геометрии – это полный четырехвершинник.

Полным четырехвершинником называется фигура, состоящая из четырех точек проективной плоскости, никакие три из которых не лежат на одной прямой, и шести прямых, соединяющих попарно эти точки. Указанные точки называются вершинами, а прямые — сторонами полного четырехвершинника. Стороны, не имеющие общей вершины, называются противоположными. В четырехвершиннике ABCD противоположными являются стороны АВ и CD, ВС и DA, АС и BD. Точки пересечения противоположных сторон называются диагональными точками, а прямые, попарно соединяющие диагональ­ные точки,— диагоналями полного четырехвершинника.

Особенностью диагональных точек является то, что они при любом расположении точек четырехвершинника не лежат на одной прямой.

Другая особенность заключается в определенной, никогда не меняющейся их связи с вершинами.

Рис. 6

1) На каждой диа­гонали полного четырехвершинника диагональные точки гармо­нически разделяют две точки, в которых эта диагональ пересекает стороны, проходящие через третью диагональную точку.

2) Две вершины, лежащие на стороне полного четырехвершинника, гармонически разделяют пару точек, состоящую из диагональной точки и точки, в которой эта сторона пересекает диагональ, проходящую через две другие диагональные точки.

По аналогии с окружностью в проективной геометрии выделяется овальная кривая второго порядка. Она задается уравнением вида .

Ряд особенностей окружности сохраняется и для нее. Так, например, любая прямая, проходящая через внутреннюю точку овальной кривой, пересекает ее в двух точках, в любой точке овальной кривой существует касательная.

Используя проективную геометрию и понятие овальной кривой, можно решать большой круг задач на элементарные построения. Например, можно построить касательную к окружности. И, учитывая особенность проективной геометрии, построения такого рода выполняются только при помощи линейки, без привлечения циркуля.

Полный и развернутый ответ с доказательствами

Возникновение проективной геометрии связано с именем известного французского математика Понселе. Он выделил как объект её изучения особые свойства геометрических фигур, которые были названы проективными. Эти свойства связаны с понятием центрального проектирования.

Рассмотрим в Евклидовом пространстве Е₃ 2 плоскости π и σ, точку О не лежащую в этих плоскостях. Пусть М – произвольная точка, принадлежащая π. Точка М´ пересечения прямой ОМ с плоскостью σ называется проекцией точки М на плоскость σ из центра О. Точке М, принадлежащей π, поставим в соответствии её проекцию М^’ на плоскость σ из центра О.

Таким образом установленное соответствие между точками плоскостей π и σ называется центральным проектированием плоскости π на плоскость σ из центра О. Аналогично определяется и проекция фигуры.

При центральном проектировании многие свойства фигуры искажаются: меняется длина отрезка, величины углов, параллельные прямые проектируются в пересекающиеся прямые, проектируя параллелограмм можно получить произвольный четырёхугольник. Более того, проектируя отрезок, можно получить луч.

Но есть и ряд свойств, которые сохраняются при любом центральном проектировании. Эти свойства Понселе и назвал проективными. Такими свойствам является, например, свойство точек лежать на одной прямой или на одной ЛВП. Однако уже свойство точки лежать между двумя другими не является проективным .

Свойства, связанные с длинами отрезков и величин углов, также не являются проективными.

Значительное место в проективной геометрии занимает введение так называемых несобственных (или бесконечно удаленных) геометрических элементов.

Дополним пространство Е₃ новыми точками, а именно: ко всем обычным точкам каждой прямой мысленно добавим ещё одну, несобственную точку. Будем считать, что две параллельные прямые имеют одну и ту же несобственную точку, а непараллельные прямые – различные. Обычные точки будем называть собственными. Прямую, дополненную несобственной точкой, назовём расширенной. Каждая плоскость имеет бесконечное множество параллельных прямых, следовательно и несобственных точек. Пусть все несобственные точки плоскости образуют несобственные прямые, а все несобственные точки пространства - несобственную плоскость. Плоскость, дополненную расширенной прямой, будем называть расширенной плоскостью.

Взаимное расположение расширенных прямых и

плоскостей.

1. Любые 2 прямые, лежащие в плоскости, пересекаются, т.е. имеют общую (собственную или несобственную) точку.

2. Любая прямая, не лежащая в плоскости, пересекает плоскость, т.е. имеет с ней общую (собственную или несобственную) точку.

3. Любые 2 плоскости пересекаются по прямой, т.е. имеют общую (собственную или несобственную) прямую.

Сформулируем понятие проективного пространства.

Пусть V – векторное пространство n+1 измерений над компонентом R. 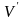– множество всех ненулевых векторов этого пространства. Непустое множество Р называется проективным пространством n-измерений, если задано отображение f: →P, удовлетворяющее следующим свойствам (аксиомам проективного пространства):

1) f – сюрьективно,

2) f(х)=f(у) ↔ и компланарны.

Элементы множества Р называются точками проективного пространства.

Зададим проективный репер на плоскости и прямой. Пусть σ – проективная плоскость. Упорядоченная система точек А₁, А₂, А₃, Е общего положения плоскости σ называется проективным репером, А_i – вершины репера, Е – единичная точка, А_i А_j – координатные прямые. Если векторы а₁, а₂, а₃, е порождающие вершины и единичную точку проективного репера выбраны таким образом, что е=а₁+а₂+а₃, то будем говорить, что система векторов согласована относительно репера R (рис. 5).

Введём понятие координат точек на проективной плоскости.

Пусть Х – произвольная точка плоскости σ, на которой задан проективный репер R. Рассмотрим какой-либо вектор х, порождающий точку Х и согласованную систему векторов. Примем векторы а₁, а₂, а₃ за базис векторного пространства, разложим вектор х по базису х=х₁ а₁+х₂ а₂+х₃ а₃ .

Т огда точка Х имеет следующие координаты Х(х₁, х₂, х₃)_R.

рис. 5

Утверждение: Проективные координатные точки х зависят от выбора как вектора х, так и системы векторов а₁, а₂, а₃, е, согласованной относительно репера R (т.е. заданием проективного репера координаты произвольной точки плоскости σ определяется с точностью до общего множителя).

Теорема: Три точки Х(х₁, х₂, х₃), Y(y₁, y₂, y₃), Z(z₁, z₂, z₃), заданные кординатами в репере R, лежат на одной прямой тогда и только тогда, когда определитель, составленный из их координат, равен нулю.

Вершины и единичная точка репера имеют координаты :

А₁(1,0,0), так как а₁=1*а₁+0*а₂+0*а₃

А₂(0,1,0), так как а₂=0*а₁+1*а₂+0*а₃

А₃(0,0,1), так как а₃=0*а₁+0*а₂+1*а₃

Е (1,1,1), так как е=1*а₁+1*а₂+1*а₃

Из теоремы следует, что точка Х(х₁, х₂, х₃) лежит на координатной прямой А₁А₂ тогда и только тогда, когда координаты точек удовлетворяют равенству:

, то есть х₃=0 и координаты точки Х(х₁, х₂, 0).

А налогично определяются и координаты точек на проективной прямой. Изображение проективного репера на прямой дано на рис. 6.

рис. 6

Рассмотрим на плоскости проективный репер R=(А₁, А₂, А₃, Е). Пусть Х – произвольная точка плоскости, отличная от А₃, а Х₃=А₂А₁∩ХА_3. Точка Х₃ называется проекцией точки Х на прямую А₁ А₂ из центра А₃. Проекции каждой точки прямой А₁ А₂ совпадают с самой точкой (рис.7).

рис. 7

Обозначим через Е₃ проекцию единичной точки репера R из центра А₃ на прямую А₁А_2. Упорядоченная система точек (А₁ ,А₂ , Е₃) на прямой А₁ А₂ образует проективный репер, который будем обозначать R₃. Аналогично вводим R₁ и R₂. Отсюда следует, если на плоскости задан репер R , то на каждой из координатных прямых возникает свой репер.

Теорема: Если произвольная точка Х плоскости, отличная от А₃ в репере R имеет координаты (х₁ , х₂ , х₃ ),то проекция Х₃ точки Х из центра А₃ на А₁ А₂ в R имеет координаты (х₁ , х₂)