Вопрос 30. Нелинейное программирование

Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор x=(x₁,x₂,…,x_n), удовлетворяющий системе ограничений

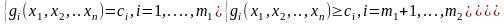
и доставляющий экстремум (наибольшее или наименьшее значение) целевой функции L=f(x₁,x₂,….,x_n), где x_j- переменные, j=1,…., n, L, f, g_i – заданные функции от n переменных, b_i – фиксированные значения. Рассматриваются, в основном, задачи, минимизирующие целевую функцию.

Нелинейное программирование применяется при прогнозировании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и т. п.

Для задачи нелинейного программирования и отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентный метод, приближенные методы решения, графический метод.

Пример. Найти точки максимума и минимума функции z=x²+2y² при условии 3х+2у=11.

Решение. Выразим из уравнения 3х+2у=11 переменную у через переменную х и подставим полученное выражение в данную функцию z. Эта функция будет иметь единственный минимум (найдем производную, получим уравнение, приравняем его к нулю) при х₀=3, при этом у₀=1. Точка (3,1) – точка условного экстремума (минимума), так как вторая производная положительная.

В рассмотренном примере уравнение связи 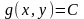оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случая это сделать сложно. Для отыскания условного экстремума в общем случае и используется метод множителей Лагранжа.

Метод множителей Лагранжа основан на построении так называемой функции Лагранжа.

Рассмотрим функцию трех переменных 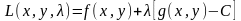. Эта функция называется функцией Лагранжа, а λ- множителем Лагранжа.

Пусть решается задача определения условного экстремума функции нескольких переменных z = f(X) при ограничениях. Составим функцию L(X)=f(X)+_i_i(X), i=1,2,…,m, которая называется функцией Лагранжа. _i— постоянные множите­ли (множители Лагранжа). Опреде­ление стационарных точек этой функции приводит к решению системы уравнений

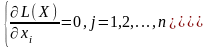
Задача нахождения условного экс­тремума функции z = f(X) сводится к нахождению локального экстремума функции L (X). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях реша­ется на основании достаточных условий экстремума — исследова­ния знака второго дифференциала d²L(X) в стационарной точке при условии, что переменные приращения x_i связаны соотно­шениями 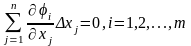, полученными путем дифференцирования уравнений связи.

Проще говоря, для нахождения условного экстремума функции двух переменных z=f(x,y) при условии g(x,y)=C требуется найти решение системы

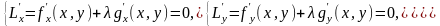
Представленная система основана на теореме.

Теорема. Если точка (х₀ ,у₀) является точкой условного экстремума функции z=f(x,y) при условии g(x,y)=C , то существует значение х₀ такое, что точка (х₀ ,у₀, λ₀) является точкой экстремума функции

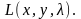
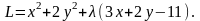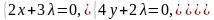Решим теперь рассмотренный выше пример методом Лагранжа. Составляем функцию Лагранжа Приравнивая к нулю ее частные производные, получаем систему уравнений Ее единственное решение х=3, у=1, λ=-2, таким образом, точкой условного экстремума может быть только эта точка. Найдя вторые производные, можно убедиться, что в этой точке заданная функция z имеет условный минимум.

Наиболее простым методом решения задач НЛП является графический метод. Если число переменных п = 2, нелинейные задачи можно ре­шать графически. Ограничения должны быть записаны в виде неравенств

Как и в случае геометрического решения задач линейного программирования, сначала необходимо построить область допус­тимых решений (ОДР) — множество точек плоскости, удовлетво­ряющих неравенствам. Но, в отличие от задач линейного программирования, здесь ОДР не обязательно будет выпуклой и может быть даже разрывной. Экстремум функции может дости­гаться и внутри области, и на границе.

После построения ОДР следует записать уравнения линий уровня целевой функции — множество точек плоскости, в кото­рых целевая функция постоянна, и опреде­лить направление возрастания (убывания) целевой функции, по­строив, например, линии уровня для разных значений С. Затем, перемещая линию уровня в нужном направлении в ОДР, найти точки области, в которых целевая функция принимает оптималь­ное значение.

Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптимальное решение может быть найдено для определенного класса целевых функций. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются вершины многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или вершине.

При решении задач нелинейного программирования для целевой функции необходимо различать понятия глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции – это ее наибольшее (наименьшее) значение из локальных максимумов (минимумов).

Наличие локальных экстремумов затрудняет решение задач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найденный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять локальный экстремум, который может существенно отличаться от глобального.