Вопрос 8. Линии второго порядка, их канонические уравнения, фокусы, директрисы., асимптоты.

Э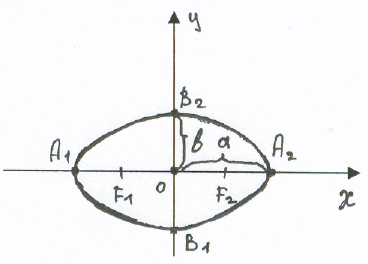 ллипсом называется множество точек

плоскости, сумма расстояний от которых до

двух данных точек F₁ и F₂ , той же плоскости,

называемых фокусами эллипса, есть величина

постоянная, большая расстояния между

фокусами. Если обозначить постоянную величину через 2а, а расстоя­ние между фокусами через 2с и выбрать систему координат так, чтобы ось Ох проходила через фокусы, а начало координат совпадало с серединой отрезка F₁F₂ , то уравнение эллипса имеет вид

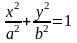, где b²=a²-c² (a>c), которое называют каноническим уравнением эллипса. a,b,c – параметры эллипса. В этом случае фокусы эллипса F₁ (-c,0), F₂ (с,0).

Начало координат О является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки А₁ (-а, 0), А₂ (а, 0), В₁ (0,- b), B₂ (0, b) называются вершинами эллипса, а длины отрезков а=ОА₂ и b=OB₂ – соответственно большой и малой полуосями. Ве­личина =с/а1 называется эксцентриситетом эллипса. Эксцентриси­тет характеризует вытянутость эллипса. =с/а=(а²-b²)/а=(1-b²/а²)

Окружность можно считать частным случаем эллипса, у кото­рого а=b, т.е. =0. Уравнение эллипса с осями симметрии, параллель­ными координатным осям, имеет вид , где х₀, у₀ – координаты центра симметрии эллипса.

Две прямые, перпендикулярные к большой оси эллипса и рас­положенные симметрично относительно центра на расстоянии а/ от него, называются директрисами эллипса. Если эллипс имеет уравне­ние , то уравнения директрис имеют вид х= -а/ и х= а/.

Справедлива теорема.

Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса.

Касательной к линии второго порядка в точке М₀ называется прямая, имеющая с линией одну общую точку. В каждой точке М₀(х₀,у₀) эллипса имеется касательная, задаваемая уравнением

( хх₀)/а² + (уу₀)/b² =1.

Г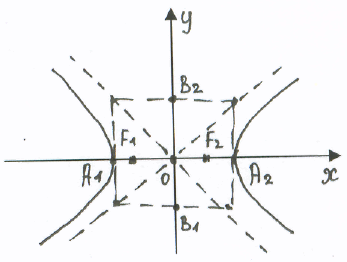 иперболой называется множество точек

плоскости, модуль разности расстояний от

которых до двух данных точек F₁ и F₂ той же

плоскости, называемых фокусами гиперболы,

есть величина постоянная, не равная нулю и

меньшая, чем расстояние между фокусами. Если обозначить постоян­ную величину через 2а, а расстояние между фокусами через 2с и вы­брать систему координат так же, как и для эллипса, то уравнение ги­перболы примет канонический вид: , где b²=c²-а², (с>а), a,b,c – параметры эллипса.

В этом случае фокусы гиперболы F₁ (-c,0) и F₂ (с,0). Оси коор­динат являются осями симметрии гиперболы, а точка О – ее центром симметрии. Гипербола пересекает ось абсцисс в точках А₁ (-а,0) и А₂ (а,0), которые называются действительными вершинами, а величина а=ОА₂ – действительной полуосью гиперболы. Точки В₁ (0,-b), В₂ (0,b) называются мнимыми вершинами гиперболы, а величина b=ОВ₂ мнимой полуосью. Прямоугольник с центром в начале координат и сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гипер­болы. Гипербола имеет две асимптоты, уравнения которых у=±(b/а)х. Асимптотой линии  называется такая прямая l, расстояние до которой от точки М стремится к нулю, когда точка М стремится по кривой  в бесконечность. Эксцентриситет гиперболы =с/а>1. Он характери­зует вытянутость основного прямоугольника гиперболы. =с/а=а²+b²/а=1+b²/а².

Уравнение гиперболы с осями симметрии параллельными коор­динатным осям, имеет вид 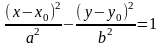, где хо, уо – коор­динаты центра симметрии гиперболы.

Если оси гиперболы равны, т.е. а=b, гипербола называется рав­носторонней. Ее уравнение имеет вид х²–у² =а². Для равносторонней гиперболы основной прямоугольник превращается в квадрат, а экс­центриситет равен 2.

Две прямые, перпендикулярные к действительной оси гипер­болы и расположенные симметрично относительно центра на расстоя­нии а/ от него, называются директрисами гиперболы. Их уравнения имеют вид х= -а/ и х= а/ для гиперболы, заданной уравне­нием. .

С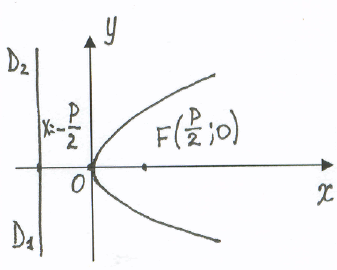 праведлива теорема: Если r – расстояние от произвольной точки гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы.

В каждой точке М₀ ( х₀, у₀) гиперболы имеется касательная, за­даваемая уравнением ( хх₀)/а² - (уу₀)/b² =1.

Параболой называется множество точек

плоскости, равноудаленных от данной точки F,

той же плоскости, называемой фокусом

параболы, и данной прямой D₁D₂, лежащей

в плоскости, называемой ее директрисой и

не проходящей через фокус. Если выбрать прямоугольную систему координат так, чтобы ось Ох проходила через фокус F (F – на положи­тельном направлении ОХ) и была перпендикулярна к директрисе D₁D₂, начало которой расположить посередине между фокусом и ди­ректрисой, то уравнение параболы в этой системе координат примет канонический вид у²=2рх, где р – расстояние от фокуса до дирек­трисы. Его называют фокальным параметром параболы. Уравнение директрисы х=-р/2, фокус F( р/2,0). Начало координат является вер­шиной параболы, а ось абсцисс – ее осью симметрии. Эксцентриситет параболы =1. Если осью симметрии параболы служит ось ординат и вершина совпадает с началом координат, то уравнение параболы имеет вид х²=2ру (р>0). Уравнение директрисы в этом случае у= -р/2, фокус F (0,р/2). Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид: (у-у₀)² = 2р (х-х₀) или (х-х₀)² = 2р (у-у₀ ), где х₀, у₀ – координаты вершины параболы. В ка­ждой точке М₀ ( х₀, у₀) параболы у²=2рх имеется касательная, зада­ваемая уравнением уу₀=р(х+х₀).

Уравнения эллипса, гиперболы и параболы в полярных коорди­натах, если полюс находится в фокусе, имеют одинаковый вид: r = p/ (1 -  cos). Это уравнение будет определять эллипс, если  < 1, пара­болу – при  = 1, гиперболу, когда  > 1. В этом уравнении для эл­липса и гиперболы фокальный параметр р связан с параметрами а и b формулой р = b²/a.

Общее уравнение линии второго порядка имеет вид: а₁₁х² + 2а₁₂ху + +а₂₂ у² + 2а₁₀ х + 2а₂₀ у + а₀₀ = 0 , где а₁₁² +а₁₂²+а₂₂² 0 и являются любыми действительными числами. Для того, чтобы при­вести общее уравнение линии второго порядка к каноническому (т.е. к простейшему), надо перейти к новой системе координат посредством поворота осей системы на определенный угол и переноса начала в нужную точку. Поворот осей исходной системы координат необходим лишь при а₁₂0 и реализуется на такой угол, чтобы уравнение линии в новой системе координат не содержало произведения разнородных переменных. Такая система координат всегда существует, а направле­ния осей этой системы называются главными направлениями линии второго порядка.

Наряду с типичными линиями второго порядка, рассмотрен­ными выше, в полученном каноническом уравнении могут скры­ваться также мнимый эллипс x²/a²+y²/b²=-1, мнимые пересе­кающиеся прямые x²/a²+y²/b²=0, действительные пересекающиеся прямые x² /a²-y²/b²= 0, параллельные x²/a²=1 или совпадающие пря­мые, параллельные мнимые прямые x²/a²= -1.

Прямые, для которых координаты направляющих векторов удовлетворяют условию Р=0, называются прямыми асимптотиче­ского направления по отношению к данной линии второго порядка, а направляющие векторы прямых – векторами асимптотического на­правления. Количество асимптотических направлений зависит от величины определителя 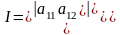. При I<0 линия второго по­рядка имеет два асимптотических направления и называется линией гиперболического типа. При I = 0 линия второго порядка имеет одно асимптотическое направление и называется линией параболического типа. При I > 0 нет действительных асимптотических направлений, линия эллиптического типа.

Если прямая l не имеет асимптотического направления по от­ношению к линии второго порядка  ( Р  0 ), то она пересекается с ней в двух точках (действительных, при Q²- PR > 0, или мнимых при Q²- PR < 0 ), либо касается ее при Q²- PR = 0 (т.е. пересекается с ней в двух совпадающих точках). Если прямая l имеет асимптотическое на­правление по отношению к  (Р = 0), то она либо пересекается с ней в одной точке ( Q, R  0), либо не имеет с  общих точек ( Q=0,R  0), либо принадлежит линии  (Q =R=0 ).

Если вектор р (р₁, р₂) имеет асимптотическое направление, то асимптоты задаются уравнением m: p₁ ( a₁₁ x + a₁₂ y + a₁₀ ) + p₂ ( a₂₁ x + a₂₂ y + a₂₀ ) = 0. Если направление вектора р (р₁, р₂ ) неасимптотиче­ское, то прямая m есть множество середин всех хорд линии , парал­лельных вектору р (р₁, р₂) . Эта прямая называется диаметром линии  , сопряженным вектору р.

Точка С (х₀ , у₀) называется центром линии , если линия сим­метрична относительно С. Линия второго порядка, имеющая единст­венный центр, называется центральной. Для того, чтобы точка С была центром линии , необходимо и достаточно, чтобы выполнялись следующие условия: a₁₁ x₀ + a₁₂ y₀ + a₁₀ = 0, a₂₁ x₀ + a₂₂ y₀ + a₂₀ = 0. Координаты центра, если он существует, являются решением этой системы.