14)Первообразная

Зная закон движения тела, можно, продифференцировав функцию перемещения тела по времени, в любой момент найти его скорость. Часто требуется решить обратную задачу, то есть найти перемещение тела, зная, как изменяется его скорость. Эта и подобные задачи решаются при помощи интегрирования – операции, обратной дифференцированию.

Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого 

Так, функция   является первообразной функции   в чем можно убедиться, поставив эти функции в определение первообразной. Функция   также является первообразной функции   

Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f.

Таким образом, для любой функции ее первообразная F определяется неоднозначно. Для того, чтобы задать ее однозначно, нужно указать точку A (x₀; y₀), удовлетворяющую уравнению y = F (x).

Теоремы первообразных

Т.1: (теорема существования) Любая непрерывная на X функция имеет первообразную F(x) на X:

Функция на X может иметь бесконечно много первообразных. Так, для первообразной является F(x) =

Т.2: Если F(x) и — две первообразные для (х) на X, то

разность между ними равна постоянной Обозначим тогда

 Пусть Применим теорему Лаг-

ранжа для на

откуда на X

15)Неопределенный интеграл

 для функции   — это совокупность всех первообразных данной функции.

где F - первообразная функции f (на промежутке); C - произвольная постоянная.

     Основные свойства

     1.     

     2.     

     3. Если   то

     4. 

Замена переменных в неопределенном интеграле

     1. 

     2. Если   - первообразная для   то

16)Таблица основных интегралов

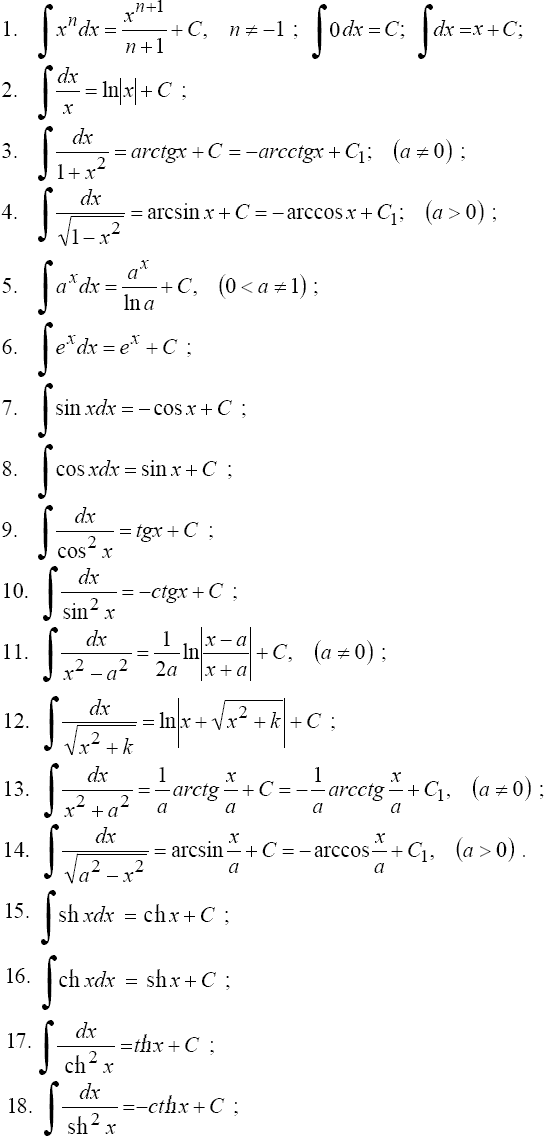
17)Интегрирование методом подстановки

 Наиболее общим приемом интегрирования функций является метод подстановки, который применяется тогда, когда искомый интеграл   не являяется табличным, но путем ряда элементарных преобразований он может быть сведен к табличному.   Метод подстановки основан на применении следующей формулы:

где x=j(t) - дифференцируемая функция от t, производная которой j'(t) сохраняет знак для рассматриваемых значений переменных.   Сущность применения этой формулы состоит в том, что в данном интеграле   переменную x заменяют переменной t по формуле x=j(t) и, следовательно, dx произведением j'(t)dt.   Приведем доказательство этой формулы. Продифференцировав левую часть форммулы, имеем

  Продифференцировав правую часть форммулы, имеем

  Таким образом формула справедлива.   Часто употребляется обратная замена переменной, т.е. подстановка t=j'(x ), dt=j'(x)dx    Пример:   Необходимо найти интеграл

  Применим подстановку: u=arctg(x), тогда

  Подставляя полученные значения в искомый интеграл получим:

  Теперь подставив значение u в полученное выражение получим решение искомого интеграла:

Замена переменной

1. Неопределенный интеграл. Один из способов интегрирования – метод замены переменной – реализуется с помощью формулы здесь переменная интегрирования х была заменена на новую переменную, t, с помощью (непрерывно дифференцируемой) функции х = φ(t). (*)

Пример

На практике часто удобнее не выражать старую переменную через новую, а, наоборот, обозначить некоторую функцию g от переменной х за новую переменную, т.е. ввести функцию  t = g(x). (**)

Тогда вместо получающейся из равенства (*) формулы dx =  , дифференцируют равенство (**) и выражают из него dx.

Пример

Вычислим    Сделаем замену переменной –3х² + 4 = t. Дифференцируя это равенство (т.е. находя дифференциал функции t(x)), получим: –6хdx = dt, откуда  Подставляя найденные выражения в интеграл, находим: где С – произвольная постоянная. Это и есть ответ.

18) Формула интегрирования по частям

Для интегрирования некоторых функций применяют формулу:  . Для правильного применения этой формулы необходимо чётко понимать, что в выражение есть  , а что есть  , и какая выгода получается от применения этой формулы. Рассмотрим несколько примеров применения этой формулы: Пример 1. Вычислить неопределенный интеграл Решение: Для наглядности можно написать одно над другим: Невооруженным глазом видно, что для применения формулы нужно принять такие обозначения: . Воспользуемся формулой интегрирования по частям (в записи много пробелов для того, чтобы каждая часть второй строки стояла четко под соответствующей частью первой строки) : Все. Формулу применили. Дальше используются уже изученные методы интегрирования. В частности, вынесение логарифма из-под знака дифференциала Ответ: