Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Омский Государственный Технический Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Математика. Аналитическая геометрия

.pdf
Скачиваний:
16
Добавлен:
30.03.2015
Размер:
433.98 Кб
Скачать
☆

Министерство образования и науки РФ Государственное образовательное учреждение высшего профессионального образования

«Омский государственный технический университет»

Аналитическая геометрия.

Омск - 2011

1

Составители: Батехина Наталья Викторовна, доцент Стругова Татьяна Михайловна, старший преподаватель

Методические указания предназначены для самостоятельной работы студентов 1 курса технических специальностей всех форм обучения

Печатается по решению редакционно-издательского отдела Омского государственного технического университета.

 

Редактор

 

 

 

ИД 06030 от

.

 

Подписано в печать

. Формат 60х84х1/16. Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ.л.

. Уч.-изд.л.

.

 

Тираж

. Заказ

.

 

Издательство ОмГТУ. 644050, г. Омск, пр-т Мира,11 Типография ОмГТУ

2

Содержание

стр.

Предисловие…………...………………………………

. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

1.Метод координат ……………………………………………………

1.1. Декартова прямоугольная система координат ……………..

1.2. Полярные координаты ……………………………………….

1.3. Преобразования декартовых прямоугольных координат на плоскости ……………………………………………………..

2.Уравнение линии на плоскости…………………………………….

2.1. Основные задачи ……………………………………………...

2.2. Уравнения прямой на плоскости (линии первого порядка)...

2.3. Прямая линия на плоскости. Основные задачи …………….

3.Линии второго порядка на плоскости ……………………………..

3.1.Окружность ……………………………………………………

3.2.Эллипс …………………………………………………………

3.3.Гипербола ……………………………………………………..

3.4.Парабола ………………………………………………………

3.5.Общее уравнение линии второго порядка на плоскости

. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТАНСТВЕ

4.Уравнение плоскости и линии в пространстве ……………………

4.1.Уравнение плоскости в пространстве ……………………….

4.2.Взаимное расположение плоскостей в пространстве .……..

4.3.Уравнение прямой линии в пространстве …………….…….

4.4.Взаимное расположение прямых в пространстве ………….

4.5. Взаимное расположение прямых и плоскостей в пространстве ………………………………………………….

4.6.Поверхности второго порядка ……………………………….

4.7.Канонические уравнения поверхностей второго порядка …

5.Методические рекомендации к выполнению индивидуальных домашних заданий ………………………………………………….

6.Индивидуальные домашние задания ………………………………

Список литературы....………………………………..………………

3

ПРЕДИСЛОВИЕ

Учебное пособие предназначено для самостоятельной работы студентов первого курса технических специальностей при изучении раздела «Аналитическая геометрия»

Данное пособие представляет собой краткий конспект лекций по данной теме. Оно содержит материал, необходимый при изучении других специальных дисциплин.

Впособии даются методические рекомендации к решению большого количества задач.

Вконце конспекта помещен довольно большой блок задач для самостоятельной работы студентов дома.

Вособый пункт внесены вопросы, которые предлагаются студентам на экзамене по высшей математике.

Мы надеемся, что данное пособие поможет студентам при изучении данной темы и будет способствовать более глубокому изучению курса высшей математики и смежных дисциплин.

. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

Основная задача аналитической геометрии заключается в изучении геометрии алгебраическими средствами.

Исходным понятием аналитической геометрии является система координат. Основным геометрическим объектам ставятся в соответствие: точке координаты, линиям и поверхностям алгебраические уравнения. Затем рассматриваются не сами объекты, а их координаты или уравнения. Такой метод получил название «метода координат». Заслуга введения этого метода принадлежит французскому ученому Рене Декарта (1596 1650).

 

 

 

 

1. Метод координат.

 

 

 

1.1. Декартова прямоугольная система координат

 

 

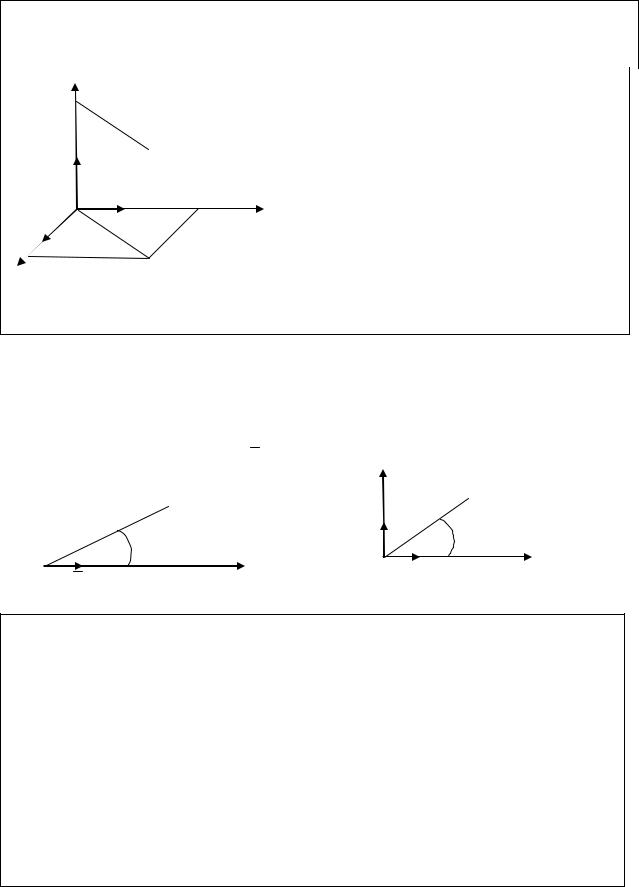
Пусть на плоскости задан декартов ортонормированный базис i , j

и

произвольная точка O. Проведем оси OX и OY как на рис.1. Эти оси` назы-

ваются координатными осями: ось OX ось абсцисс, OY ось ординат.

 

Y

 

 

 

Точка О начало координат.

 

y

 

M x,y

 

Плоскость, на которой задана система

 

 

 

координат, называется координатной

 

 

 

 

 

j

 

 

 

плоскостью. Теперь любой точке плоскости

 

 

 

соответствует пара действительных чисел

 

 

 

 

 

 

О

i

x

Х

x,y координаты точки и наоборот.

 

 

 

Рис.1

 

 

 

 

 

 

 

4

 

Таким образом, введение системы координат позволяет установить взаимно однозначное соответствие между всем множеством точек плоскости и множеством всех пар действительных чисел. Декартова прямоугольная

 

 

z

 

 

система координат в пространстве

 

 

 

 

вводится заданием декартова ортонорми-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

рованного базиса

 

,

 

,

 

и некоторой

 

 

 

 

 

 

 

M x,y,z

i

j

k

 

 

 

 

 

 

 

точки O (начала координат).

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

Проведем оси OX, OY, OZ как на

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

рис.2. Ось OX ось абсцисс, OY ось

 

 

 

 

 

 

 

ординат, OZ ось аппликат.

 

 

 

 

 

j

 

i

 

 

Теперь каждой точке пространства

x

 

Рис.2

соответствует тройка действительных

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

чисел x,y,z координаты точка М и наоборот, каждой тройке чисел соответствует вполне определенная точка пространства.

1.2. Полярные координаты

На практике часто используется полярная система координат. Полярная система координат (рис.3) задается точкой О полюсом, лучом

ОР полярной осью и ортом e направления ОР. y

 

 

M r,

y

 

 

 

 

 

M

 

 

 

 

 

 

 

 

 

r

 

 

 

r

 

 

 

 

 

 

j

 

 

 

 

 

 

 

o

 

 

 

 

o

 

 

 

 

x

x

e

P

 

i

 

 

Рис.3

 

 

Рис.4

 

Числа rи называют полярными координатами точки M , записывают:

M r, , гдеr полярный радиус, полярный угол, при этом

0 2 , а полярный радиус r 0, .

В этом случае каждой точке плоскости (кроме точки О) соответствует единственная пара чисел r, и обратно.

На рис.4 видно, что прямоугольные координаты x и y точки М опреде-

x rcos ,

ляются из прямоугольного треугольника следующим образом:

y rsin .

5

Полярные координаты точки М выражаются через декартовы

 

r

x2 y2 ,

координаты из того же треугольника:

 

 

 

Определяя

 

 

y

 

tg

.

 

 

 

 

 

x

величину , следует учесть четверть,

в которой лежит угол и

что .

 

 

 

 

1.Параллельный перенос.

 

Y

M

 

Пусть на плоскости задана ДСК

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(прямоугольная система координат) XOY.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j

Y1

 

Под параллельным переносом осей

 

 

O

 

 

 

 

 

i

 

X

 

координат будем понимать переход от

 

 

 

 

 

 

 

 

 

 

 

системы XOY (назовем ее старой) к новой

 

 

 

 

 

 

 

j

 

 

системе X OY , при котором меняется

 

 

 

 

 

 

 

 

 

 

 

1

1

1

 

 

 

 

 

 

O1

 

X

начало координат, а направление осей и

 

 

 

 

Рис.5

i

 

 

 

 

 

 

 

 

 

масштаб остаются неизменными (рис.5).

Пусть точка O1 начало новой системы координат имеет в системе

XOY координаты a,b . Точка M имеет координаты x,y в системе координат XOY и x1,y1 системе X1OY1 1.

Заметим, что орты направлений OX и OX1, а такжеOY иOY1 равны между собой.

Рассмотрим векторы OO1, OM,и O1M . OM x i y j,

O1M x1 i y1 j, OO1 a i b j. Так как OM OO1 O1M, то

x i y j a i b j x1 i y1 j, т.е. x i y j x1 a i y1 b j.

x x1

a,

Следовательно,

Полученные формулы позволяют выражать

y y1

b.

старые координаты x,

y через новые координаты x1,y1 и наоборот.

2. Поворот вокруг начала координат.

Под поворотом осей вокруг начала координат на угол будем понимать

6

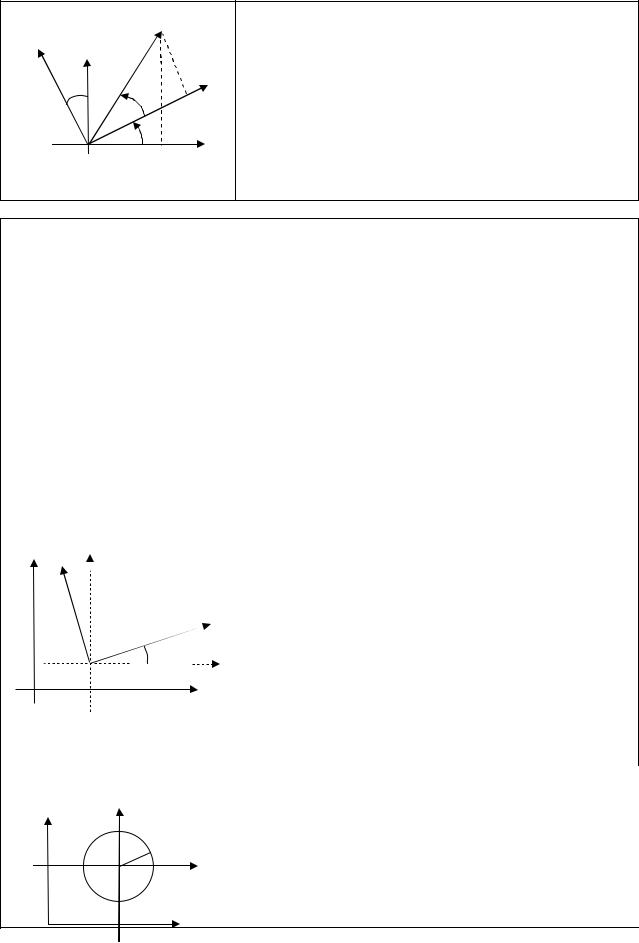
M

Y1 Y r

 

 

X1

Рис.6

O X

такое преобразование системы координат, при котором обе оси поворачиваются на один и тот же угол , а начало координат и масштаб остаются без изменений.

Пусть новая система координат X1OY1 получена из системы XOY поворотам вокруг точки Oна угол (рис.6). ТочкаM произвольная точка плоскости, x,y ее координаты в

старой системе XOY и x ,y в новой системе XOY .

Введем две полярные системы координатOX и OX с общим полюсом O.

Полярный радиус r

одинаков в обеих системах и образует полярные углы

и соответственно с осями OX и

OX ,

где полярный угол в новой

системе координат.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

По формулам перехода от полярной системы координат в ДСК имеем:

x r cos ,

 

x

 

rcos

 

cos

 

sin

 

sin

 

,

x

 

rcos

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

т.к.

 

 

 

 

y r sin ,

 

x rsin cos cos sin ,

y rsin ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x x cos y sin ,

Полученные формулы называются формулами

то

 

 

y x sin y cos .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

поворота осей. Они позволяют выражать старые координаты через новые и наоборот новые через старые.

Y

Y

 

 

 

 

Если новая система координат X OY

 

1

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

 

Y

 

 

 

 

получена из старой системы XOY путем

 

 

 

 

 

 

 

параллельного переноса на вектор

 

a,b и

 

 

 

 

 

OO1

b

 

 

X

 

 

последующим поворотом осей на угол (рис.7),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sin a,

 

 

O O

 

X

 

 

то получим формулы:

x xcos y

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

O

a

 

X

 

 

 

 

 

 

 

 

y x

sin ycos b,

 

 

 

 

выражающие старые координаты x,y через ее

 

 

Рис.7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

новые координаты x

,y

 

 

 

 

 

Уравнение окружности на рис.8 есть: x a 2

y b 2 R2.Уравнение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

 

этой же окружности в системе координатXOY

 

 

 

 

 

 

2

y

2

R

2

.

 

 

 

 

 

 

 

b

R

 

 

выглядит: x

 

 

 

 

 

 

 

 

 

 

 

 

Если задано уравнение линии в системе

 

 

 

X

 

 

 

 

 

 

координат XOY , то чтобы получить уравнение

 

 

 

O

 

 

 

 

 

 

 

этой же линии в другой системе координат,

 

 

O

a

X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7

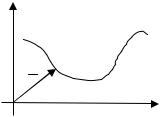
Рис.8

достаточно подставить в уравнение вместо xи y

их выражение через новые координаты.

2.Уравнение линии на плоскости

2.1.Основные понятия

1.Понятия об уравнении линии на плоскости.

Пусть на плоскости задана ДСК, некоторая линия Lи произвольная точка M x,y , лежащая на ней. Точку M x,y будем называть текущей точкой, а ее координаты x,y текущими координатами.

Определение. Уравнением линии на плоскости XOY называется уравнение F x,y 0 с двумя текущими координатами, которому удовлетворяют координаты x,y тех и только тех точек, которые лежат на линии Lи не удовлетворяют координаты точек, не лежащих на этой линии.

Для того чтобы определить лежит ли точка M0 x0, y0 на линии,

достаточно проверить удовлетворяют ли ее координаты данному уравнению. Для этого надо подставить координаты точки x0, y0 в уравнение F x,y 0.

В случае получения верного числового равенства делают вывод, что точка M0 x0, y0 лежит на линии L, в противном случае точка не принадлежит

данной линии.

Уравнение F x,y 0 не всегда определяет линию. Так, например, урав-

нению x2 y2 0 удовлетворяют координаты только одной точкиO 0,0 , а

уравнению x2 y2 2 0 не удовлетворяют координаты ни одной точки плоскости.

2. Параметрические уравнения линии на плоскости.

Пусть на плоскости задана в ДСК линия L. Переменные координатыx,y точек удобно представлять как функции некоторой третьей

x t ,

переменной (или параметра, например, времени) t: гдеt t1,t2

y t ,

и t , t непрерывные функции параметра t.

2. Векторное уравнение линии.

Y

M

r

O X

8

Любой вектор перпендикулярный к
9

 

Линию на плоскости можно задать векторным

 

уравнением

r

 

r

t , где t скалярный

 

переменный параметр. Каждомуt0 соответствует

 

единственный радиус-вектор

r0

 

r

t0 . При

Рис.9

изменении параметраt t1,t2 конец радиус-

вектора опишет некоторую линию (рис.9).

 

 

 

 

 

 

 

 

 

 

Векторному уравнению r r t в системе координат XOY соответствуют

x x t ,

два скалярных уравнения проекций вектора на оси OX иOY .

y y t

Таким образом, уравнения проекций векторного уравнения на оси есть ее

параметрические уравнения.

Векторное уравнение и параметрические уравнения имеют механический смысл. Если точка перемещается на плоскости, то данные уравнения называются уравнениями движения, линия перемещения траекторией движения, параметрt время движения.

Замечание. Всякой линии на плоскости соответствует уравнение

F x,y 0. Всякому уравнению F x,y 0, вообще говоря, соответствует линия на плоскости.

2.2. Уравнения прямой линии на плоскости (уравнения первого порядка)

1. Векторное уравнение прямой линии.

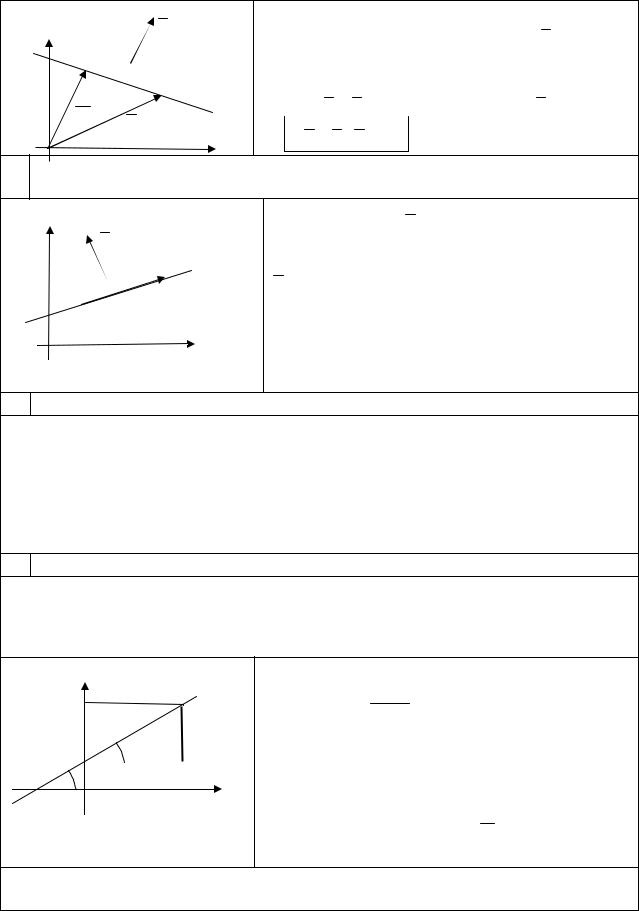
1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Положение прямой вполне определено на

Y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

плоскости, если задана точка M0 прямой и вектор ,

M0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

параллельный этой прямой (рис.10). Вектор

 

 

 

 

 

 

M

 

 

 

 

 

 

 

 

 

 

 

 

 

 

назовем направляющим вектором данной

 

r0

 

 

 

 

 

 

прямой.

 

 

 

 

rM

 

 

 

 

O

 

 

 

 

 

 

 

X

 

 

 

Если прямая линия задана точкой M0 x0,y0,z0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.10

 

 

и вектором m,n, p , M x,y,z текущая точка

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

прямой,

r0

и

r

радиус-векторы точек M0 и M , то

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

Так как вектор

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

r0

M0M

M0M

коллинеарен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

, то

 

 

 

t

 

,тогда

r

 

r0

t

 

 

векторное уравнение прямой, где

вектору

 

M0M

 

 

t скалярный параметр (каждому значению параметра t соответствует точка на прямой).

2)

 

 

 

 

 

n

 

прямой (рис.11), будем называть

Y

M0

 

нормалью к прямой и обозначать

n

A,B .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M

 

 

Если вектор n , то n M0M и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M0M

r

 

r0

 

, тогда выполняется

n

M0M 0

r

0

 

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и

r

 

r0

,

n

0.

 

 

Рис.11

 

 

 

OX

2.Уравнение прямой линии, проходящей через данную точку, перпендикуляр но данному вектору.

Y

 

 

n

A,B

 

 

Если вектор

n

A,B перпендикулярен

 

 

 

 

 

 

 

 

 

 

 

 

вектору M0M x x0,y y0 (рис.12), то

 

 

 

 

 

 

 

 

 

 

 

 

 

M x,y

n

 

M0M

0.

 

M

0

x ,y

0

 

Следовательно,

A x x0 B y y0 0,

 

 

 

0

 

 

 

 

 

 

 

 

 

 

O

 

 

 

 

 

X

гдеAи B координаты вектора нормали.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.12

3.Общее уравнение прямой линии.

Вуравнении A x x0 B y y0 0 раскроем скобки и сгруппируем слагаемые: Ax Ax0 By By0 0. Обозначим Ax0 By0 C и получим

Ax By C 0,

где A,B,C любые числа, AиBопределяют координаты

 

 

вектора нормали (уравнение первой степени, соответствующее кривой первого порядка).

4. Уравнение прямой линии с угловым коэффициентом.

Выразим yчерез xиз общего уравнения прямой линии Ax By C 0.

By Ax C,

y

A

x

C

.

Обозначим

A

k,

 

C

b , тогда y kx b.

 

 

 

 

 

 

B B

 

B

 

B

Y

M

b

 

 

y b

 

 

x

 

 

O

x X

 

Рис.13

С другой стороны из треугольника на

рис.13 tg y b , следовательно, x

x tg y b, y x tg b. Обозначим

tg k и

y k x b,

где k угловой

 

 

 

коэффициент прямой.

Замечание: k tg A, где A и B

B

координаты вектора нормали.

Угловой коэффициент k характеризует расположение прямой линии на координатной плоскости.

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности