1Правило Лопиталя. Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть  или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

2) Признаки постоянства функции

Необходимое и достаточное условие постоянства функции у = f(x) выражается равенством у' = 0

Функция у = f(x) называется возрастающей в промежутке (а, b), если для любых двух значений x1 и х2 из неравенства x1 < x2 следует неравенство f(x1) < f(x2)(а).

Функция у = f(x) называется убывающей в некотором промежутке, если для любых двух значений, принадлежащих этому промежутку, из неравенства х1 < х2 следует неравенство f(x1) > f(x2) (б).

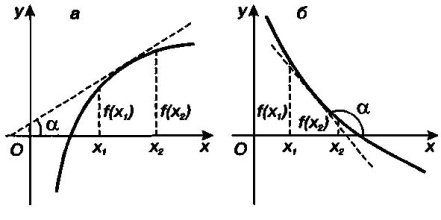
Достаточное условие возрастания или убывания функции выражается следующей теоремой.

Теорем. Если на данном промежутке производная положительна, то функция возрастает в этом промежутке; если производная функции отрицательна, то функция убывает.

Замечание. Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции у = f(x) образует с осью Ох острый угол a (tg а > 0), то функция возрастает в этом промежутке (а). Если касательная к графику образует с осью Ох тупой угол a (tg а < 0), то функция убывает (б).

3) Признаки монотонности функции

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Пусть дана функция   Тогда

функция   называется возраста́ющей на  , если

.

функция   называется стро́го возраста́ющей на  , если

.

функция   называется убыва́ющей на  , если

.

функция   называется стро́го убыва́ющей на  , если

.

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Точки экстремума

Точки экстремума – в математике это понятие определяет максимальное или минимальное значение функции в конкретном множестве. Точка максимума – точка, в которой достигается максимальное значение, точка минимума, соответственно, минимальное.

Локальный минимум и максимум

Необходимые условия существования локальных экстремумов

Из леммы Ферма вытекает следующее:

Пусть точка   является точкой экстремума функции  , определенной в некоторой окрестности точки  .

Тогда либо производная   не существует, либо  .

Достаточные условия существования локальных экстремумов

Пусть функция   непрерывна в   и существуют конечные или бесконечные односторонние производные  . Тогда при условии

 является точкой строгого локального максимума. А если

то   является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке 

Пусть функция   непрерывна и дважды дифференцируема в точке  . Тогда при условии

 и 

 является точкой локального максимума. А если

 и 

то   является точкой локального минимума.

4)Признак выпуклости и вогнутости функции

График дифференцируемой функции называется

выпуклым (выпуклым вверх) на (a, b), если он расположен на (а, b) ниже касательной, проведенной в любой его точке; вогнутым (выпуклым вниз), если он расположен выше любой своей касательной (рис. 10.9).

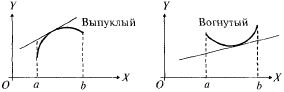
Т: (достаточный признак выпуклости, вогнутости) Пусть функция дважды дифференцируема на (а, b). Если   на (а, b), то график — выпуклый, — вогнутый

Необходимое и достаточное условие существование точек перегиба

Точка перегиба функции   внутренняя точка x₀ области определения  f , такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и   является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

Условия существования

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки  , имеет в   точку перегиба, то  .

Достаточное условие существования точки перегиба: если функция   в некоторой окрестности точки     раз непрерывно дифференцируема, причем   нечётно и  , и   при  , а  , то функция   имеет в   точку перегиба.