Площадь криволинейного сектора.

            Пусть кривая Г задана в полярной системе координат уравнением

где   - неотрицательная и непрерывная на отрезке   функция. Тогда плоскую фигуру G, огранич2енную кривой Г и, быть может, отрезками двух лучей, составляющих с полярной осью углы   и   (рис 3), назовемкриволинейным сектором.

            Утверждение 2. Криволинейный сектор G – квадрируемая фигура, площадь которой S выражается формулой

32)Длина дуги в декартовых координатах

Длина дуги в прямоугольной системе координат

 О: Под длиной дуги кривой понимается предел, к которому стремится длина вписанной в нее ломанной, если длина самого большого ее звена стемится к нулю.

Допустим, что кривая определена уравнением , при этом представлена в качестве непрерывно дифференцируемой функции на . Разделим ее на частей посредством точек с абсциссами и проведем через данные точки хорды (рис. 18.9, а). В результате имеем вписанную ломанную с длиной  ее -го звена

 Здесь L, составляет Из определения длины дуги следует  Поскольку правая часть представляет собой интегральную сумму для функции , то

 

Пример: Найти длину дуги окружности , если (рис. 18.9, б).

 

 18.3.2. Длина дуги кривой в параметрической форме

Предположим, что уравнение кривой L определено в параметрической форме: , здесь функции являются непрерывно дифференцируемыми на , при этом на . В этом случае

 

Пример: Вычислить длину окружности, определенной параметрическими уравнениями при

 

18.3.3. Длина дуги в полярных координатахДопустим, что уравнение кривой L в полярных координатах , при этом функция является непрерывно дифференцируемой на . С помощью формул перехода от полярных координат к декартовым и рассматривая в качестве параметра угол , запишем параметрические уравнения кривой В этом случае

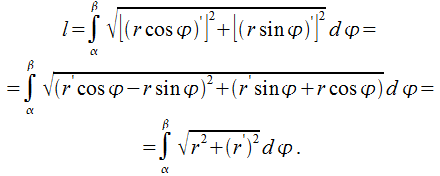
 Пример: Определить длину дуги логарифмической спирали (рис. 18.10).

 

 

33)Объем и поверхность вращения

34)Применение определенного интеграла к решения физических задач

Пусть к движущейся по прямой точке приложена направленная вдоль этой прямой переменная сила F=f(x), где f(x) есть непрерывная функция от х – координаты движущейся точки. Работа силы F при передвижении точки от a до b равна

где a=x₀<x₁<…<x_n=b, ?x_j=x_j+1-x_j

в силу непрерывности функции f(x) произведение   близко к истинной работе на отрезке [x_j; x_j+1], а сумма таких произведений близка к истинной работе на отрезке [a; b], и притом тем ближе, чем меньше наибольший из всех ?x_j.

№ 4.

К движущейся по прямой точке приложена направленная вдоль этой прямой сила F=2х-1, где х – координата движущейся точки. Вычислите работу силы F по перемещению точки от 0 до 3. (слайд 17)

Решение: 

2. Масса стержня переменной плотности (слайд 18)

Будем считать, что отрезок [a; b] оси Ох имеет массу с переменной линейной плотностью  , где  - непрерывная на отрезке [a; b] функция. Общая масса этого отрезка  , где a=x₀<x₁<…<x_n=b, ?x_j=x_j+1-x_j

№ 5. Вычислить массу стержня на отрезке от 0 до 2, если его плотность задаётся функцией   (слайд 19)