37)Производные высших порядков
функции y =f (x) есть также функция от x:
y' =f ' (x)
Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) илипроизводной функции f(x) второго порядка. Пользуясь обозначением
можем написать
Пример.
Очень удобно пользоваться также обозначением
,
указывающим, что функция y=f(x) была продифференцирована по x два раза. Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функции y=f(x) или производной функции f(x) третьего порядка и обозначается символами
.
Вообще n-я производная или производная n-го порядка функции y=f(x) обозначается символами
Теорема Шварца
Поверхностный интеграл Примеры решения и оформления задач контрольной работы
Если
функция двух переменных f(x,y) имеет в
точке (x0,y0) непрерывные частные производные
2-ого порядка 
,
то эти смешанные частные производные
совпадают.
1*) Докажем Теорему 1. Используем формулы Лагранжа 2-ой раз.
теорема
доказана.
38)Полное приращение и полный дифференциал функции нескольких переменных
Полным
приращением функции двух переменных 
в
точке 
называется
выражение 
.
Предположим,
что в точке
и
некоторой ее окрестности функция z = f(x,y)
имеет непрерывные частные производные
первого порядка 
и 
.
Выразим через них полное приращение 
:
(1)
где 
заключено
между 
и 
, 
заключено
между 
и 
,
рис. 11.
Так как по предположению частные производные непрерывны, то:
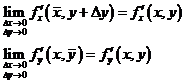Û 
(по
связи функции, её предела и бесконечно
малой), где g1 и g2 –
бесконечно малые при Dх®0 и Dу®0,
то есть при 
.
Таким
образом, полное приращение 
функции
выразилось
следующим
образом:
(2)
Каждое
из слагаемых ΙΙ является б.м. более
высокого порядка малости относительно 
.
Действительно,
Þ 
при
.
Аналогично 
Þ 
+
при
.
Ι слагаемое – линейное относительно Dx и Dy, оно является главной частью полного приращения Dz.
Функция z = f(x,y), полное
приращение Dz которой
в данной точке (x;y) может
быть представлено в виде суммы двух
слагаемых: выражения, линейного
относительноDx и Dy,
и величины, бесконечно малой более
высокого порядка малости, чем 
,
называется дифференцируемой
ФНП в данной точке;
главная часть ее полного приращения,
линейная по приращениям аргументов,
называется полным
дифференциалом ФНП:
39)Дифференцирование композиции функции нескольких переменных
Приращение функции
Функция,
дифференцируемая в точке 
при 
В этом случае дифференциал функции в точке :
-
частные производные, вычисленные в
точке
Дифференцирование
композиции
1.
Если 
то
2.
Если
Однородная
функция степени k
40)Дифференцирование неявных функций и функций заданных параметрически
Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у'-3(1· у+х· у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).
21.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть 
Найти у'х.
Решение:
Имеем x't=3t2,
y't=2t.
Следовательно, у'х=2t/t2,
т. е. 
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, 
Тогда 
Отсюда
т.
е.