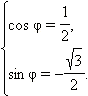12)Тригонометрическая форма комплексного числа

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть   и φ = arg z. Тогда по определению аргумента имеем: 

Отсюда получается 

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Пример 1

Записать число   в тригонометрической форме.

Решение

Найдём модуль этого числа:   Аргумент данного числа находится из системы  Значит, один из аргументов числа   равен   Получаем:  Ответ.

Модуль комплексного числа

Длина вектора, изображающего комплексное число, называется модулем этого комплексного числа. Модуль всякого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + bi обозначается |a + bi|, а также буквой r. Из чертежа (фиг. 5) видно, что

Модуль действительного числа совпадает с его абсолютным значением. Сопряженные комплексные числа а + bi и a - bi имеют один и тот же модуль.

Аргумент

Угол φ между осью а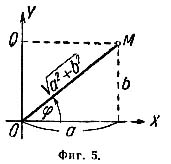 бсцисс и вектором ОМ, изображающим комплексное число а + bi, называется аргументом комплексного числа а + bi. На фиг. 6 вектор OM изображает комплексное число -3 -3i. Угол   являемся аргументом этого комплексного числа. Каждое не равное нулю комплексное число* имеет бесчисленное множество аргументов, отличающихся от друга на целое число полных оборотов (т. е. на 360°k где k — любое целое число). Так, аргументами комплексного числа – 3 – 3i являются все углы вида 225° ± 360°k, например 225° + 360° = 585°, 225° - 360° = - 135°. Аргумент φ связан с координатами комплексного числа а + bi следующими формулами (фиг. 5):

       Однако ни одна из них в отдельности не позволяет найти аргумент по абсциссе и ординате (см. примеры). Пример 1.Найти аргумент комплексного числа - 3 – 3i. По формуле (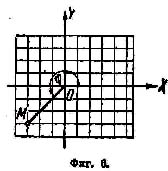 2)tgφ = -3/-3 = 1. Этому условию удовлетворяют как угол 45˚, так и угол 225˚. Но угол 45˚ не является аргументом числа - 3 – 3i. (фиг. 6). Правильный ответ будет φ = 225˚ (или —135˚, или 585˚ т. д.). Этот результат получится если учесть, что абсцисса и ордината данного комплексного числа отрицательны. Значит, точка M лежит в третьей четверти. Другой способ. По формуле (3) находим  Формула (4) показывает, что sin φ тоже отрицателен. Значит, угол φ принадлежит третьей четверти, так что φ = 225˚ ± 360˚k.

Формула Муавра

Формула Муавра для комплексных чисел   утверждает, что

для любого 

13)Показательная форма комплексного числа

 Рассмотрим тригонометрическую форму комплексного числа   ::

.

(1)

   Используя формулу Эйлера, преобразуем правую часть равенства (1):

(2)

      Запись вида (2) называется показательной формой комплексного числа.

Формула Эйлера

Существует также показательная форма комплексного числа связанная с тригонометрической по формуле Эйлера:

.

(9)

Данное соотношение легко доказать, если произвести разложение экспоненты в ряд Тейлора:

.

(10)

Представим ряд в виде суммы четных и нечетных членов последовательности:

.

(11)

Рассмотрим более подробно мнимую единицу в четной и нечетной степенях. Выражение (1) задало  , тогда , в свою очередь  . Таким образом можно рекурентно записать:

.

(12)

Построим аналогичным облразом рекурентное соотношение для нечетных степеней:  тогда  , в свою очередь  , получим:

.

(13)

Таким образом выражение (11) с учетом (12) и (13) принимает вид:

.

(14)

В выражении (14) первая сумма по четным степеням дает разложение в ряд Тейлора функции косинуса, а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции синуса. Таким образом, получено доказательство справедливости формулы Эйлера (9). Используя формулу Эйлера можно сделать ряд важных замечаний: Замечание 1:

.

(15)

Замечание 2:

.