3. Метод фазових траєкторій

Метод фазових траєкторій (фазового простору, фазової площини) – графоаналітичний метод наближеного дослідження нелінійних систем. Суть метода полягає в оцінці поведінки системи за допомогою наочних геометричних уявлень – фазових параметрів. Фазовий простір (простір станів) – простір в прямокутній системі координат, якими є вихідна змінна та (n-1) її похідних. Кількість фазових координат дорівнює порядку системи n, тому для системи другого порядку (n=2) фазовий простір є 2-х вимірним, тобто перетворюється у фазову площину. В цьому випадку термін “фаза” має таке ж значення, що і “стадія”, тобто розвиток, зміна стану. Точка з координатами (x_i, x_j) називається зображуючою, а лінія, по якій вона переміщується при зміні стану системи – фазовим портретом. Це сукупність траєкторій, які визначають множину груп початкових умов та розв’язок диференціальних рівнянь системи. Фазові траєкторії дають повне уявлення про характер процесів в системі, крім часових оцінок, тому що час з розгляду процесів виключається.

Якщо розглядати в системі стабілізації відхилення то усталеному стану буде відповідати точка , тобто початок координат. Цей стан відповідає так званій особливій точці. Різним фазовим траєкторіям відповідають різні особливі точки. Наприклад, для лінійних стійких систем всі фазові траєкторії асимптотично стягуються в початок координат, а у випадку нестійких систем – прямують в нескінченінсть.

З розгляду наведеного матеріалу можна зробити висновок, що найбільш зручним є метод фазової площини. Запишемо диференціальне рівняння системи другого порядку:

(1.1)

Будемо вважати, що х – вихідна координата системи і приймемо х₁=х, тоді:

(1.2)

Рівняння (1.1) запишемо у вигляді двох рівнянь 1-го порядку:

або (1.3)

Розділимо друге рівняння в (1.3) на перше:

(1.4)

Після інтергування отримуємо рівняння фазових траєкторій:

(1.5)

де: С₁, С₂ – постійні інтегрування. Вид функції залежить від коефіцієнтів а_i, які визначають корені характеристичного поліному системи:

(1.6)

корені рівняння:

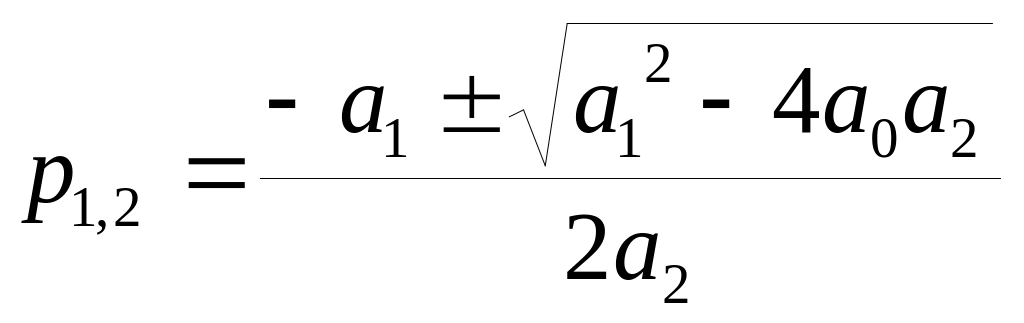(1.7)

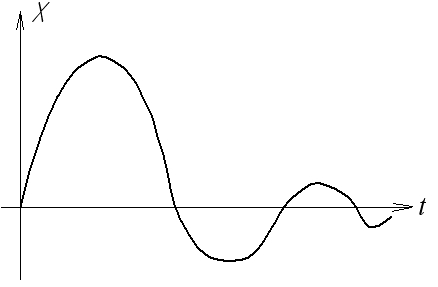
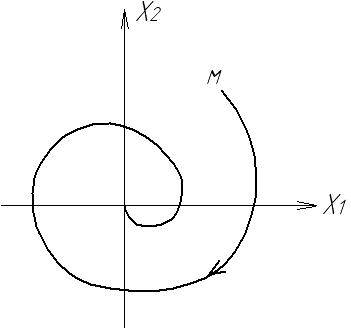
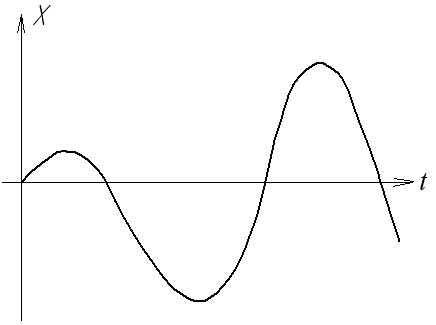
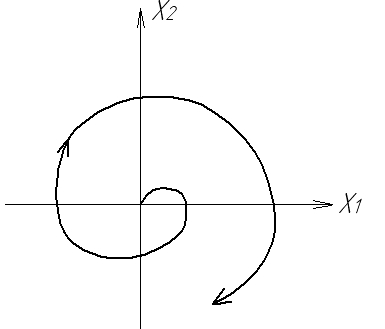
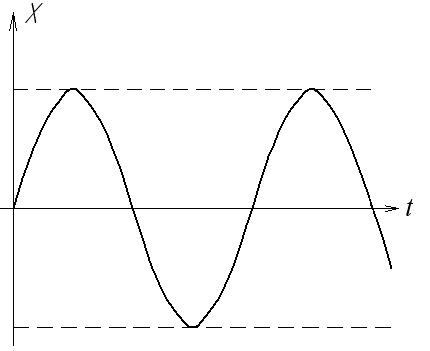
В методі фазової площини головним, визначальним моментом є те, що кожному перехідному процесу в системі відповідає своя фазова траєкторія. Вид коренів рівняння (1.6) розглядався в розділі, присвяченому стійкості автоматичних систем (частина перша). На рис. 1.4 показана відповідність перехідних процесів і фазових траєкторій НЛС, що відповідає комплексним попарно спряженим кореням з від’ємною (а) та додатною (б) дійсними частинами і уявними (в). Можна знайти також інші перехідні процеси, наприклад, аперіодичні та відповідні фазові портрети.

а)

б)

в)

Рис.1.4. Перехідні процеси і фазові траєкторії НЛС

а) стійкої; б) нестійкої; в) на межі стійкості

Аналіз перехідних процесів та відповідних фазових портретів НЛС приводить до таких результатів:

• стійкому коливальному процесу відповідає фазова траєкторія, яка збігається до початку координат (рис.1.4,а). Особливою точкою тут є стійкий фокус;

• нестійкому коливальному процесу відповідає фазова траєкторія, яка віддаляється від початку координат, особливо точка – нестійкий фокус (рис.1.4,б);

• періодичному процесу (автоколиванням) відповідає замкнена фазова траєкторія (коло або еліпс), яка називається граничним циклом (рис.1.4,в), особлива точка – центр.

Для інших фазових траєкторій особливими точками можуть бути стійкий або нестійкий вузол, сідло.

За графіком граничного циклу можна наближено визначити параметри автоколивань: частота характеризується відношенням відрізків на осях х₂ до х₁, а амплітуда дорівнює відрізку на х₁.

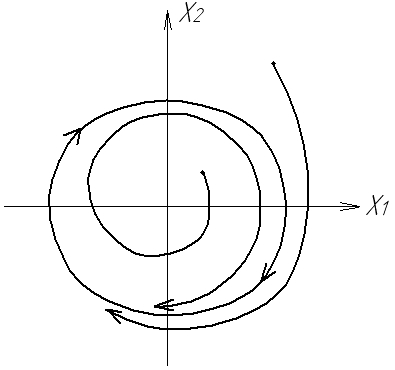
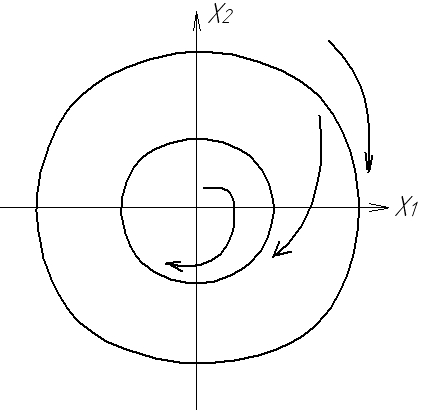
Фазові траєкторії НЛС мають свої особливості. Це викликано тим, що для лінійної системи характер особливої точки повністю визначає її поведінку при будь-яких відхиленнях від стану рівноваги, тобто стійкість лінійної системи не залежить від величини збурення і ця властивість зберігається у всіх точках фазового простору. Для НЛС характер особливої точки визначає поведінку фазових траєкторій лише поблизу точки рівноваги. Може бути такий випадок: стан рівноваги НЛС нестійкий, перехідний процес розбіжний, але він може перейти в стійкий граничний цикл (рис.1.5).

а) б) в)

Рис.1.5. Фазові траєкторії нелінійних систем

а) стійкий граничний цикл; б) нестійкий граничний цикл; в) два граничних цикли

Якщо в нелінійній системі є суттєві зони нечутливості та сухого тертя, то усталеному стану відповідає не один режим, а область, і особлива точка “витягується” в особливу лінію(рис.1.6).

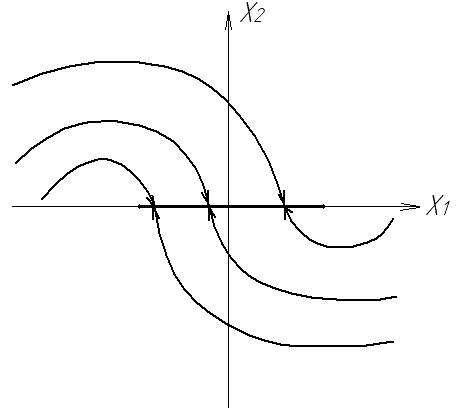
Рис.1.6. Фазові траєкторії НЛС із зоною нечутливості і сухим тертям

В залежності від особливостей НЛС в них можуть бути автоколивання:

• з м’яким режимом збудження, коли після включення завжди система переходить в режим автоколивань не залежно від початкових умов і зовнішніх збурень;

• з жорстким режимом збудження, коли для виникнення автоколивань, які відповідають стійкому циклу, необхідно створити достатньо велике початкове відхилення. Наприклад, зображуюча точка знаходиться поза стійким граничним циклом, а під впливом зовнішніх сигналів вона може перейти на цей цикл або переміститись всередину цикла, і автоколивання затухнуть.

Фазовий портрет НЛС може мати кусково-лінійні або розривні характеристики, складатись з кількох областей з різними фазовими траєкторіями. В цьому випадку на фазовому портреті є лінії перемикання, які відділяють одну область від іншої.

Розроблено метод наближеної побудови фазових портретів НЛС, який дістав назву методу припасовування (зшивання), коли характеристики нелінійностей подаються у вигляді кусково-лінійних залежностей (ламаною лінією). Це відповідає тому, що в правій частині рівняння фазових траєкторій буде набір кількох лінійних функцій для лінійних дільниць характеристики нелінійної ланки. В процесі зміни х₁ та х₂ відбувається заміна однією функції на іншу в момент проходження через точки зламу. В результаті фазова характеристика розбивається на ряд дільниць, в межах кожної з яких їх рівняння є лінійними і легко інтегруються. Таким чином, точки зламу кусково-лінійної характеристики відповідають лінії переключення, зміни правої частини рівняння (рис.1.7), де показана лінія перемикання АВСD для системи другого порядку.

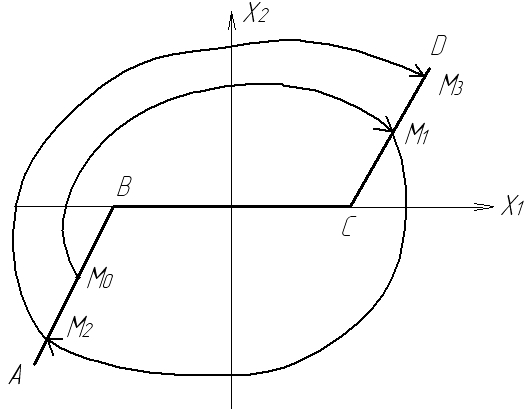
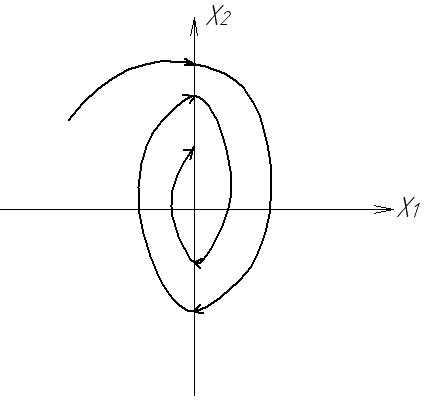
Рис.1.7. Лінія перемикання для системи 2-го порядку

Рис.1.8. Фазовий портрет системи з релейним елементом

Для НЛС з релейним 2-х позиційним елементом фазовий портрет показаний на рис.1.8. Лінія перемикання співпадає з віссю х₂ (х₁=0). Для НЛС з релейними елементами існує ковзний режим, коли зображаюча точка переміщується по лінії переключення, наближаючись до початку координат (“ковзає”). Перехідний процес в релейній системі протікає як в неперервній системі. При цьому релейний елемент переключається з достатньо великою частотою, а ковзний режим (коливання навколо лінії переключення) створює ефект вібраційної лінеаризації.

Крім метода припасовування (зшивання) для побудови фазових портретів НЛС використовується метод ізоклін – кривих з однаковим нахилом фазових траєкторій, які проходять через точки цих кривих.

Головним методом дослідження НЛС є використання ЕОМ: визначається кількість і характер можливих станів рівноваги, кількість граничних циклів і їх взаємне розташування, що дає можливість оцінити сукупність можливих режимів роботи системи. Виконуються також розрахунки для найбільш важливих початкових умов.