Ч1.Вопрос20. Поле. Следствия из аксиом. Отсутствие делителей нуля. Характеристика поля; ее простота. Подполя и расширения полей. Изоморфизм колец (полей).

Опр: Полем называется множество P в котором определены операции + * (замкнуты) и выполняются следующие аксиомы:

1) Р – не нулевое кольцо.

2) Умножение коммутативно ab=ba, a,b прин Р.

3) Множество Р с исключенным нулем есть группа по умножению.

Примеры: Множество рациональных чисел, действительных, комплексных. C\R – не является полем. P={0} – не явл.

Опр: Пусть задано поле Р; подмножество Р’ – которое само явл-ся полем, тогда Р’ называют подполем поля Р, а Р – расширение поля Р’.

Следствия из аксиом ? 1)  единичный элемент, что a*1=1*a=a, для a прин Р;

2)  обратный элемент a^-1, что a*a^-1 =1, для a прин Р;

3) для a прин Р, a0,n прин Z; выполняется (a^-1)ⁿ=(aⁿ)^-1

Отсутствие делителей нуля – никакое поле не содержит делителей нуля – Док-во: пусть ab=0, но a0 | умножая обе части на a^-1 => слева (a*a^1-)b=1*b=b, справа а^-1*0=0, т.е. b=0. Отсюда следует что во всяком поле любое равенство можно сократить на общий множитель, отличный от нуля. В самом деле если ac=bc и c0, то (a-b)c=0, => a-b=0, т.е. a=b. ■.

Характеристика поля; ее простота. Будем обозначать сумму n – единиц 1+1+..+1=n*1. Наименьшее натуральное число n, такое что n*1=0 называется характеристикой поля. Если при любом n, n*1 не = 0, то говорят что характер-ка поля равна нулю.

Замечание:  поля характеристики нуль. Прим: рац. числа, комплек-х, множ-во A{0,1} характеристика 2.

Теорема: Если поле P имеет конечную характеристику n, то n простое число.

Замечание: Из Т. не следует сущест-е полей характе-ки p, где p – простое число, а следует лишь, что не существует полей составных характеристик.

Подполя и расширения полей.

Пусть в поле P некоторая часть его элементов, составляющая множество P’, сама оказывается полем по отношению к тем операциям, которые определены в поле Р, т.е. для a,b прин P’ содержащиеся в поле P элементы a+b,ab,a-b и, при b0, a/b принадлежат к P’. Тогда P’ называется подполем поля Р, а Р – расширением поля P’. Понятно, что нуль и 1 поля Р будут содержаться в поле Р' и служить для P’ нулем и единицей. Так, поле рациональных чисел явл-ся подполем поля действительных чисел; все числовые поля будут подполями поля комплексных чисел.

Изоморфизм колец (полей). Два кольца К и К’ (поле Р и P’) называются изоморфными, если  взаимно однозначное отображение и К->K’ (P->P’), что для  элементов из К (Р) выполняются равенства:

Существование суммы произведения, след-ет из аксиомы кольца (поля). Такое отображение  - называют изоморфизмом и изоморфные поля с точки зрения алгебры одинаковы.

Пример: пусть К – множество всех действительных чисел (К->R), K’ –множество всех точек на прямой. Сложение для точек на прямой введем сложение как сложение векторов, а умножение, как умножение модулей.

В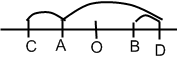 качестве взаимного отображения  можно выбрать следующее правило – каждому действительному числу ставим в соответствие точку удаленную от фиксированного начала координат на к единиц.

Пример: Множество точек на плоскости и комплексные числа.

Замечание: 1) если К изоморфно К’ - КK' => K'K 2) KK’, K’K’’ => KK’’ 3) Если К и К’ изоморфны, то кол-во элементов в них совпадает.