Вопросы по алгебре:

Часть 1 – 1 семестр

15. Простые и двойные суммы. Их Свойства. Линейные преобразования неизвестных; их умножение. Получить вид матрицы произведения линейных преобразований.

16. Умножение матриц, его свойства. Единственность единичной матрицы. Доказать отсутствие обратных матриц у вырожденных матриц.

17. Обратная матрица (существование, единственность).

18. Решение матричных уравнений вида AX=B, XA=B. Теорема Крамера.

19. Алгебраические операции. Примеры. Группы, кольца (определения, примеры). Делители нуля. Возможность сокращения.

20. Поле. Следствия из аксиом. Отсутствие делителей нуля. Характеристика поля; ее простота. Подполя и расширения полей. Изоморфизм колец (полей).

21. Кольцо многочленов от одной переменной. Степень произведения. Отсутствие делителей нуля. Многочлены, имеющие обратные.

22. Алгоритм деления с остатком (доказать единственность). Делители многочлена. Доказать свойства делимости (не менее 5 свойств).

23. НОД. Доказать алгоритм Евклида. Сформулировать его следствие.

24. Число НОД двух многочленов. Взаимно простые многочлены; их свойства.

25. Корни многочленов. Деление на (x-c). Теорема Безу. Метод Горнера. Теорема Виета.

26. Кратные корни. Производная многочлена; ее степень. Теорема о понижении кратности корня при дифференцировании. Следствия.

27. Число корней многочлена в произвольном поле. Равносильность двух понятий равенства. Формулировка теоремы существования корня. Следствия. Поле разложения.

28. Сформулировать основную теорему алгебры комплексных чисел. Разложение на линейные множители над полем C. Число корней многочлена с комплексными коэффициентами. Неприводимые многочлены и каноническое разложение над полем C.

29. Доказать сопряженность корней многочлена с действительными коэффициентами. Следствия. Неприводимые многочлены и каноническое разложение над полем R.

30. Отделение корней C. Критерий отсутствия кратных корней.

31. Определение линейного пространства. Некоторые следствия из аксиом. Основные примеры линейных пространств.

32. Два определения линейной зависимости. Их равносильность. Примеры. Связи между линейной зависимостью системы и её подсистем.

33. Теорема о максимальных линейно независимых подсистемах (о базисах). Примеры.

34. Основная теорема о линейной зависимости.

35. Следствия из основной теоремы о линейной зависимости для конечных систем векторов.

36. Конечномерные линейные пространства (определение, примеры). Следствия из основной теоремы о линейной зависимости для конечномерных линейных пространств.

37. Изоморфизм линейных пространств; его свойства; примеры. Теорема об изоморфизме.

Ч1.Вопрос15. Простые и двойные суммы. Их Свойства. Линейные преобразования неизвестных; их умножение. Получить вид матрицы произведения линейных преобразований.

Опр.: Сумма вида , где i – индекс суммирования, называется простой суммой. Пример: ■ Свойства простых сумм:

1.Простая сумма не зависит от обозначения индекса суммирования.

2.Постоянный множитель можно выносить за знак суммы. , с не завис-т от i

Двойные суммы. Сумма простых сумм обозн-ся = a₁₁+a₁₂+..+a₂₁+a₂₂+..+a_kn всего слагаемых n*k. Пример: . Свойства двойных сумм: 1,2 такие же как и у простых. 3. порядок сумм можно менять, для доказательства достаточно заметить, что справа и слева стоят суммы всех эл-тов a_ij■

Матрицы линейных преобразований неизвестных Опр1: пусть даны 2 системы неизв-х:

x₁ x₂ x₃ x_n (1) старые неиз-е. y₁ y₂ y₃ y_n (2) новые неизв-е.

Переход от старых неиз-х к новым которые совершаем по формулам x₁=a₁₁y₁+a₁₂y₂+..+a_1ny_n; x₂=a₂₁y₁+a₂₂y₂+…+a_2ny_n; x_n=a_n1y₁+a_n2y₂+..+a_nny_n – наз-ся линейный преобразованием неизвестных, числа a_ij считаем комплексными.

Опр2: Матрица А состоящая из a_ij называют матрицей линейного преобразования.

Пример: x₁=3y₁-y₂+3y₃; x₂=y₁-y₃; x₃=4y₂+y₃;

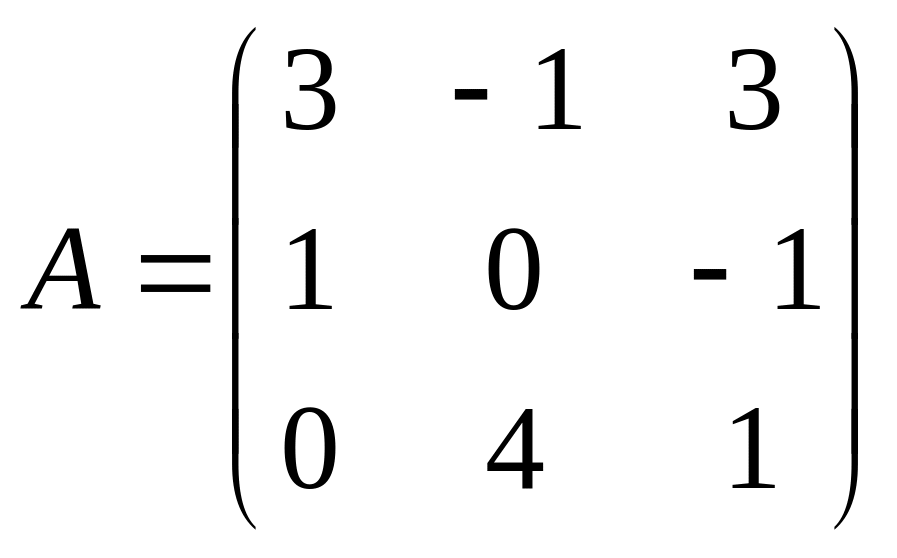
Матрица определяет 1 линейное преобразование (ЛП) и обратное не является ЛП.

Опр3: Два линейных преобразования неизв-х называют равными, если равны их матрицы т.е. в записи линейного преобр-я обозначения неизвестных роли не играют.

Опр4: Линейное преобр-е неизв-х которое получается в результате последовательного выполнения двух линейных преобр-й называется произведением этих преобразований.

x1, x2 .. xn (1) y1, y2 .. yn (2)

(3)

z₁, z₂ ..z_n

(4)	Чтобы сов-ть последов-но лин-е преобр-я (3) (4) надо выразить yi из (4) и подставить в (3), чтобы их перес. yi (4)->(3)

=> x_i=a_i1y₁+a_i2y₂+..+a_iny_n= из (4) y_k выраж-ся через переменную z_n; y_k= ; x_i= ; Поменяем местами порядок суммирования => ;

C=A*B; 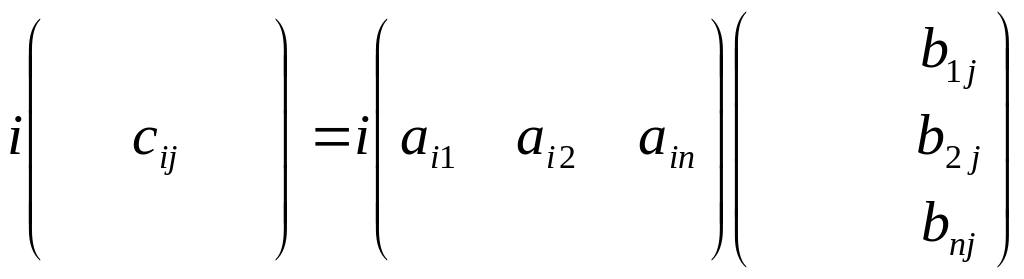; Элементы i – строки умн-ся на эл-ты j столбца и элементы складываются. ■

Пример:

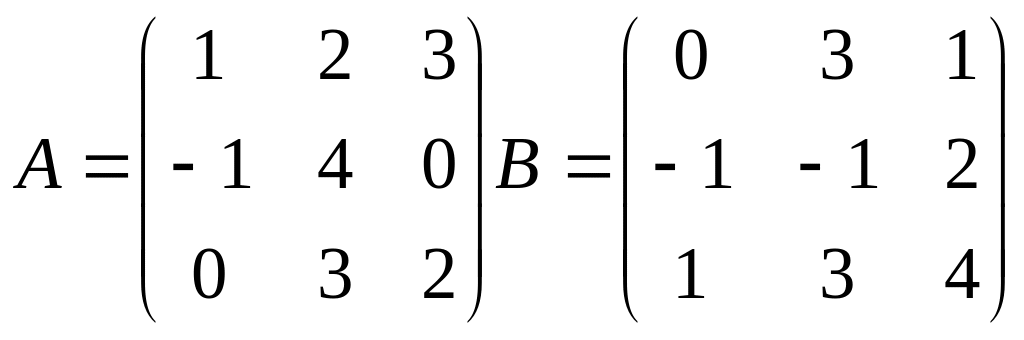
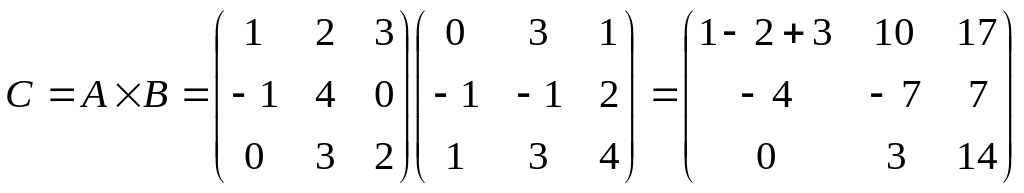
С₁₁=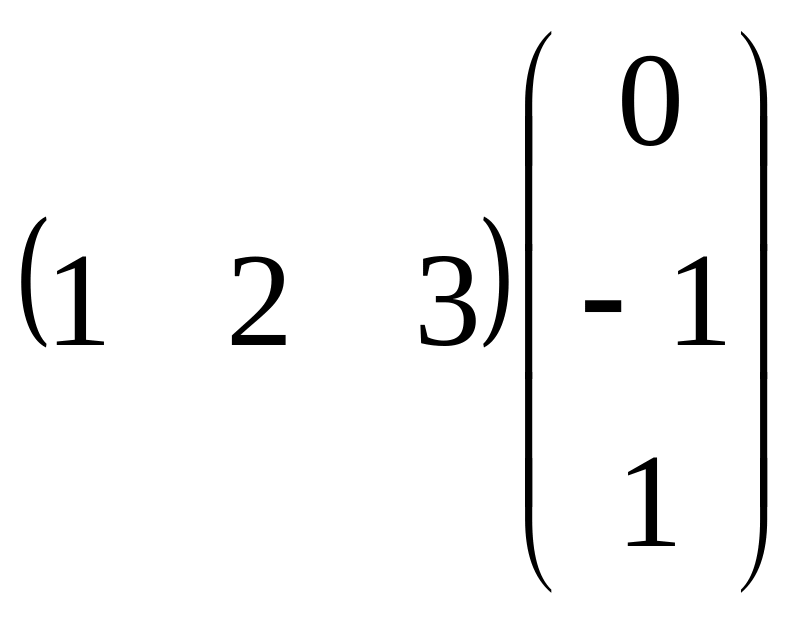 =1*0+2*(-1)+3*1=1…С₁₂

Свойства умножения матриц:

1. Умножение матриц не коммутативно. ABBA

2. Умножение матриц ассоциативно. A(BC)=(AB)C

3.  единичная матрица. AE=EA=A, для  A – квадратной матрицы.

Матрица тождественного перобр-я имеет вид