Экзаменационный билет № 9

1. Второй закон термодинамики. Обратимые и необратимые процессы. Цикл Карно и его КПД. Неравенство Клаузиуса. Энтропия и термодинамическая вероятность. Формула Больцмана. Основное уравнение термодинамики. Термодинамические потенциалы. Критерии устойчивости термодинамической системы. Третий закон термодинамики. Флуктуации. Статистический смысл второго начала термодинамики.

2. Простейшие одномерные задачи квантовой механики. Прямоугольная потенциальная яма и гармонический осциллятор. Прямоугольный потенциальный барьер. Туннельный эффект. Уровни энергии при двух и многих минимумах потенциальной энергии.

1. Второй закон термодинамики. Обратимые и необратимые процессы. Цикл Карно и его КПД. Неравенство Клаузиуса. Энтропия и термодинамическая вероятность. Формула Больцмана.

Сущ-т неск-ко равноправных формулировок II-го начала термодинамики:

I.Опр-ние Клаузиуса: тепло само по себе не может переходить от тела менее нагретого к телу более нагретому.

II.Опр-ние Планка: нельзя построить такую периодически действующую машину, единственным рез-том действия к-й было бы превращение теплоты полностью в работу.

III.Опр-ние Карно: КПД идеальной машины не зависит от вида рабочего тела и опр-ся изм-м температуры.

IV.Опр-ние Кельвина: нельзя построить тепловую машину, к-я бы превращала в работу тепло наименее нагретого в термодинамической системе тела.

V.Вечный двигатель 2-го рода невозможен.

Обратимые и необратимые процессы.

Обратим. процесс - к-й может происх-ть в прямом и обратном напр-х, при этом при обратном процессе термодинамическая система (ТДС) проходит через те же самые состояния, что и при прямом. Т.к. в реальных усл-х происх-т рассеяние энергии, то в действ-ти обратимых процессов не существует. Они исп-ся в кач-ве модели при изучении ТДС.

Цикл Карно и его КПД.

Цикл Карно предст-т собой замкнутый цикл, в к-м 1 2: изотермич. расширение; 2 3: адиабатич. расширение; 3 4: изотермич. сжатие; 4 1: адиабатич. сжатие; А – полезно осуществлённая работа; - тепло, отдаваемое нагревателем при изотермич. расширении; - тепло, получаемое холодильником при изотермич. сжатии.

К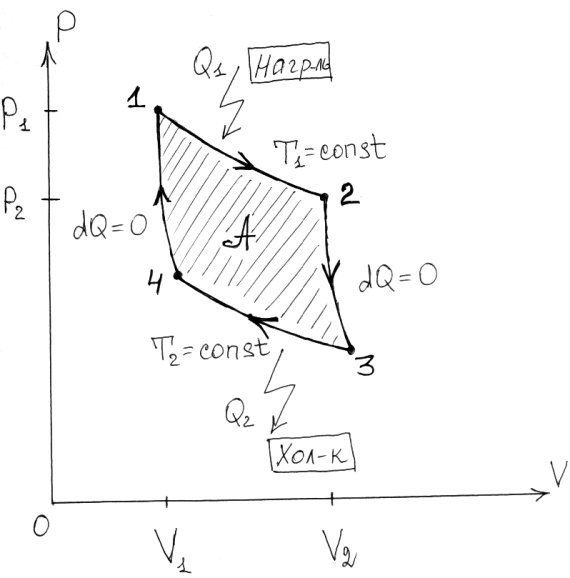 ПД цикла Карно: =А/ =( - )/ , иначе =

КПД идеальной машины, работающей по циклу Карно, зависит от температур

нагр-ля ( ) и хол-ка ( ), причём чем , тем и чем , тем .

Нер-во Клаузиуса.

Расс-м обратимый (идеальный) цикл Карно:

=1- / ; =1- / ; 1- / = 1- / ; / -1= / -1; / = / ; / = / ; / - / =0.

В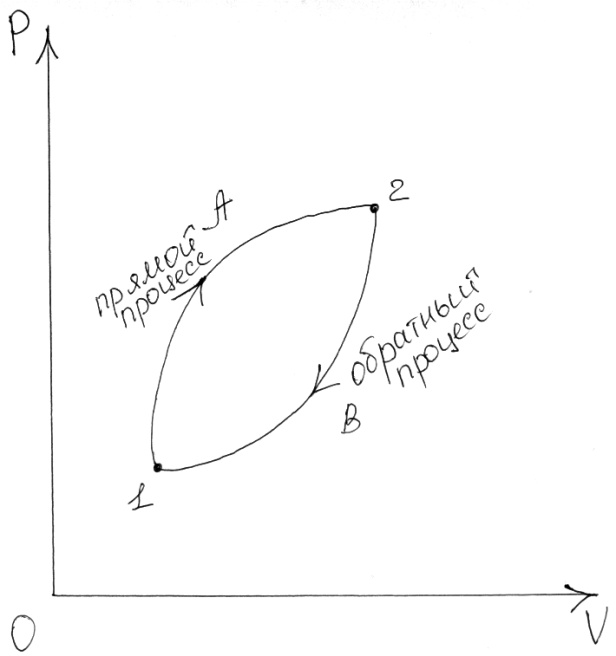 ведём понятие приведённой теплоты: =- тепло, к-е отдаётся хол-ку, взятое с отриц. знаком, т.е. отр-ное кол-во теплоты, к-е получает ТДC от хол-ка. Тогда: / + / =0(1).Т.о. в идеальном цикле Карно сумма приведённых теплот равна нулю.

В случае необр. цикла Карно: =1- / =1- / ; =1- / ; (R – реальное)

< ; 1- / <1- / ; / > / ; / > / ; / - / <0; т.к. =- , то / + / <0(2). Т.о. сумма приведённых теплот в реальных усл-х для необр. цикла Карно меньше нуля.

Объединяя (1) и (2), получаем нер-во Клаузиуса: / + / 0(3).

Энтропия.

В общем случае (3) можно записать так: или же 0; ; ; Вводим следующую величину: , где S – функция состояния ТДС, называемая энтропией. Физ.смысл энтропии: она является мерой тепловой неработоспособности нагр-ля, т.е. харак-т степень обесценивания тепловой энергии. Иначе: энтропия харак-т степень близости ТДC к своему равновесному состоянию, харак-т меру беспорядка ТДС.

Св-ва энтропии: 1) при необр. процессах энтропия увеличивается( ); 2)при обратимых процессах энтропия не изменяется ( ); при любых процессах энтропия не убывает.

Термодинамическая вероятность.

ТД-вероятность - – физ. величина, равная числу микросостояний, из к-х может быть реализовано данное макросостояние. Системе, находящейся в наиболее равновесном состоянии, соотв-т максимальное число микросостояний.

=N!/n!(N-n)!, где N- общее кол-во частиц в ТДС.

Рассм-м сосуд с молекулами, снаружи вакуум.

Е сли сосуд открыть, мол-лы будут вылетать. Процесс необр., . Есть какая-то этого процесса. Когда система расширяется в вакуум, то беспорядок системы возрастает, . Т.о. энтропия явл-ся функцией ТД-вероятности.

Формула Больцмана.

При объединении двух систем с разными и общие: и . Очевидно, что ~ln . C учётом коэфф-та Больцмана получ. ф-ла Больцмана: =kln , к-я опред-т связь между энтропией и ТД-вероятностью: энтропия пропорц-на логарифму ТД-вероятности.

2. Простейшие одномерные задачи квантовой механики. Прямоугольная потенциальная яма и гармонический осциллятор. Прямоугольный потенциальный барьер. Туннельный эффект. Уровни энергии при двух и многих минимумах потенциальной энергии.

1. Движение свободной частицы, т.е. движущейся в отсутствии внешних полей, значит силы на нее не действуют, тогда потенциальная энергия частицы U(x)=const и ее можно принять = 0. Значит полная энергия совпадает с Ek, тогда уравнение Шредингера:

∂² Ψ/∂x² + 2mEΨ/ħ² = 0 (1). Частным его решением является Ψ(х) = Ае^ikx, где А,к = const, с собственным значением энергии: E = ħ²k²/2m (2).Тогда зависящая от времени волновая функция: Ψ(х,t) = Аe ^{– iωt + ikx} = Ae ^{– (i/ħ) (Et - px)} (3), где ω=E/ħ и k=p_х /ħ. Функция (3) представляет плоскую монохроматическую волну де Бройля. Из (2) следует, что зависимость Е от р_х : E = ħ²k²/2m = р_х²/2m, т.к. волновое число k может принимать любые > 0 значения, тогда Е свободной частицы - любые значения, т.е. ее энергетический спектр непрерывный. Т.о. такая частица описывается (3). Этому соответствует не зависящая от t плотность вероятности обнаружения частицы в данной точке пространства: |Ψ|² = ΨΨ^* = |A|², т.е. все положения частицы в пространстве равновероятны.

2. Частица в одномерной прямоугольной потенциальной яме (рис.1), т.е. в силовом поле.

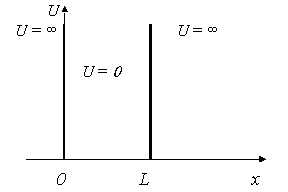∂ ² Ψ/∂x² + 2mEΨ/ħ² = 0 (4), его решение ищем в виде: Ψ(х) = Ае^ikx + Bе ^{– ikx} (5), где k = 2mE/ħ² (6). Частица не проникает за пределы ямы, тогда за ее пределами и на границах Ψ=0. На левой границе: Ψ(0)=А+B=0; для правой: Ψ(L) = А(е^ikL – е ^{– ikL}) = A sin kl = 0 (7), выполняется при kl=nπ (8), т.е. k=nπ/l, тогда, учитывая (6): E_n=n²π²ħ²/2ml², (n=1,2, …) (9), значит Е принимает определенные дискретные значения (уровни энергии), т.е. квантуется. n-главное квантовое число. Подставив в (7) (8), найдем собственные функции: Ψ_n(х)=A sin nπх/l, А находим из условия нормировки: А²∫ sin² nπх/l dx = 1. В результате интегрирования: А=(2/l)^1/2, тогда

Ψ_n(х) = (2/l) ^1/2 sin nπх/l, (n=1,2, …) (10). Графики функций (10), соответствующие уровням энергии (9) – на рис.2/а. На рис.2/б – плотность вероятности обнаружения частицы. Наприм., при n=2 частица не находится в середине ямы, а одинаково часто прибывает в ее левой и правой частях.

Из (9) следует, что энергетический интервал между двумя соседними уровнями равен: (11)

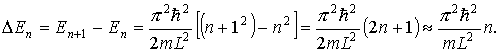
Для электрона при L=10^-1 м: ∆E_n ≈ 10^-35 n Дж ≈ 10^-16 n эВ, т.е. уровни Е расположены столь тесно, что спектр считают непрерывным. Если L ≈ 10^-1 м, то ∆E_n ≈ 10^-17 n Дж ≈ 10^-2 n эВ, т.е. явно дискретные значения Е (линейчатый спектр).

Гармонический осциллятор. Осциллятор - физическая система, совершающая колебания. Если колебания описываются синусоидальной функцией, то такой осциллятор - гармонический. Примеры классических гармонических: математический, физический и пружинный маятники. Движение их происходит под действием квазиупругой силы

F = - kx, х - отклонение осциллятора от положения равновесия, к - упругая постоянная. Его потенциальная энергия: U=kx²/2=mω₀²x²/2 (12) (ее зависимость на рис.3), ω₀ - собственная частота колебаний осцил.,m – масса частицы. Значит потенциальная яма – параболическая.

П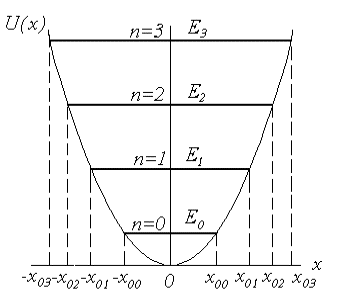 онятие осциллятора применяется также к немеханическим колебательным системам. В частности, электрический колебательный контур является электрическим осциллятором. В квантовой механике понятие силы не используется. Поэтому аналогом классического осциллятора в ней будет квантовый гармонический осциллятор, состояние которого описывается уравнением Шредингера с потенциальной функцией вида (12). Такие квантовые колебания совершают атомы в молекулах, ионы в узлах кристаллической решетки твердого тела (фононы), валентные электроны в твердых телах относительно ионного остова (плазмоны). Ур.Шредингера для одномерного случая: (13) 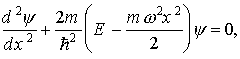                             Е - полная энергия квантового осциллятора. (13) имеет решения только при: E_n=(n + 1/2)ħω₀, (n=0,1,2, …). Энергетические уровни квантового гармонического осциллятора находятся на равных расстояниях друг от друга (рис.3). Т.о. полная энергия его принимает определенные дискретные значения. Наименьшее: E₀=1/2ħω₀ – энергия нулевых колебаний, ее наличие означает, что частица не может находиться на дне потенциальной ямы.

Прямоугольный потенциальный барьер. Туннельный эффект.

В областях I, II, III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Например, выход электронов из металлов, распад атомных ядер. Ур.Шредингера:

∂² Ψ/∂x² + 2m(E-U)Ψ/ħ² = 0, где U(x)=[0, x<0 – для области I; U, 0≤ X ≤d – для II; 0, x>d – для III]. Для I и III: ∂² Ψ_1,3/∂x² + 2mEΨ_1,3/ħ² = 0.

Для II: ∂² Ψ₂/∂x² + 2m(E-U)Ψ₂/ħ² = 0. Их решения (14):

Ψ₁(х) = А₁е^ikx + B₁е ^{– ikx} (для I); Ψ₂(х) = А₂е^ikx + B₂е ^{– ikx} (для II);

Ψ₃(х) = А₃е^iβx (для III); где k=(2mE)^1/2/ħ, β=(2m(E-U))^1/2/ħ. А₁ – амплитуда падающей волны; B₁ – амплитуда отраженной; А_2, B₂ – падающей и отраженной на границе х=d. В обл. III отраженной волны не будет, т.е. B₃ =0. Падающая волновая функция нормируется так, чтобы А₁ = 1. Остальные коэф-ты рассчитываются по отношению к А₁ , используя в (14) следующие условия (15). Эффект прохождения частицы через барьер - туннельный эффект. Для его описания используется понятие коэф-та прозрачности