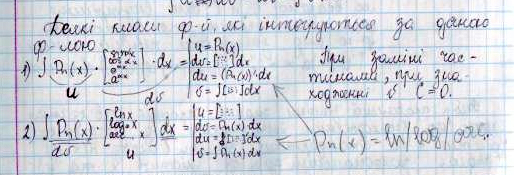20 Геометрична інтерпритація диференціалу

Нехай y=f(x). Проведемо дотичну до графіка цієї функції в точці M(x,y).

L_o – кут нахилу дотичної в данній точці. (tgL_o=y’(x)). Дамо аргументу приріст ∆x, при цьому функція отримає приріст ∆у=Nm₁. Із трикутника MNT бачимо, що

NT = tgL_o*MN=y’(x)* ∆x (згідно умови). Таким чином NT=dy(x)

Зауваження на малюнку ∆у->dy буває і навпаки.

Згідно означення диференціалу правила обчислення диференціалів легко отримати із правил обчислення похідних.

d(u*v)=udv+vdu

d(u/v)=(vdu-udv)/v²

d(u+v)=du+dv

d(u+c)=du(c=const)

31 Основна формула інтегрального числення(Ньютона – Лейбніца) , заміна у визначеному інтегралі та інтегрування частинами.

Теорема: Нехай функція f задовольняє умову:

1. f інтегрована на [a,b]

2. f має первісну на [a,b]

Нехай А – будь-яка первісна f на [a,b], тоді

Тема 21

Невизначений інтеграл(з первісної)

Нехай f:R->R диференційована. Це означає, що операція диференціювання ставе у відповідність ф-ї f ф-ю f’. Одна із мождивиї фізичних трактовок цієї операції – визначення швидкості руху по ф-ї, яка задає відстань за даний час. Природньою є і обернена операція 0 визначення шляху по відносній швидкості як ф-ї від часу. Повертаючись до поняття похідної, остання операція є операцією знаходження ф-ї за її похідною. Буквою J будемо позначати деякий інтервал R. Крім того будемо вважати, що у випадку закритого інтервалу похідні ф-ї, що розглядаються, неперервні на кінцях інтервалу.

Нехай f:J->R. Ф-я F:J->R називається первісною ф-ї f на J, якщо для будь-якого х є J існує f”(x) I F”(x)=f(x). Із Df1 слідує, що F(x) неперервна на J.

Зауваження: Деякі прості ф-ї можуть не мати первісних, виражених через прості ф-ї.

Нехай первісна для ф-ї f(x) існує. В цьому випадку ця первісна не визначена єдиним чином. Зрозуміло, що якщо F’(x) – первісна цієї ф-ї. Крім того легко доводиться той факт, що якщо F(x) I G(x) – дві первісні однієї і тієї самої ф-ї, то вони відрізняються лише на константу. Вираз F(x)+C описує всі первісні для даної ф=ї f(x).

Df2. Невизначеним інтегралом ф=ї f на J називається набір всіх її первісних. Позначається INTEGr(f(x)dx). Integr(f(x)dx)=F(x)+C, f(x’)=F(x). f(x) – підінтегральна ф-я. Процедура визначення первісної або невизначеного інтегралу назив інтегруванням ф-ї.

Тема 22, 23

Елементарні властивості невизначених інтегралів(22)

Елементарні властивості невизначених інтегралів, таблиця інтегралів(23)

(випливають із значень диференціалу та інтегралу при умові існування первісної)

1. INTEGRAL(a * f(x) dx) = a*INTEGRAL(f(x) dx)

2. INTEGRAL (f(x)+g(x) dx) = INTEGRAL(f(x) dx + INTEGRAL (g(x) dx

3. INTEGRAL (f’(x) dx) = f(x) + C або INTEGRAL (f’(x) dx) = INTEGRAL(d(f(x))) = f(x)+C;

4. d(INTEGRAL (f(x)dx))/dx = dy/dx=y’

ТАБЛИЦЯ ОСНОВНИХ ІНТЕГРАЛІВ

Тема 24

Заміна у невизначеному інтегралі.

ТЕОРЕМА 1

Нехай F – первісна ф-ї f на R (або деякому інтервалі), тобто INTEGRAL(f(x) dx) = f(x)+C. І нехай ф-я j(x) має похідну j’(x) в кожній точці цього інтегралу, то INTEGRAL(f(j(x))*j’(x)dx) = f(j(x))+C.

ЗАУВАЖЕННЯ: Теорема 1 застосовується зазвичай одним із 2-х способів: 1)Якщо підінтегральну ф-ю можна представити у вигляді добутку 2-х ф-й, одна з яких є складною, а інша – похідною внутрішньої ф-ї і зовнішня ф-я має відому первісну то маємо INTEGRAL(f(j(x))*j’(x)) = INTEGRAL(f(j(x))*d(j(x))) = f(j(x))+C. (внесеня внутрішньої ф-ї під знак диференціалу); 2)Якщо підінтегральна ф-я є складною і не може бути представлена так як вказано в п.1., але внутрішня ф-я має обернену, то внутрішню ф-ю слід замінити певним чином: INTEGRAL(j(x)dx = I (x) = j(t), dx=j’(t)*dt I = INTEGRAL(j(j(t))*dj’(t)*a).

Вибір правильної заміни значно спрощує розв’язання задачі на знаходження інтегралу. Слід запам’ятати кілька стандартних замін.

ТЕОРЕМА 2. Нехай ф-ї u: (a,b) -> і v: (a,b) ->R такі, що x є (a,b) існує. Крім того u*v’ має первісну на даному інтервалі, тоді ф-я u’*v також має первісну на (a,b) і справедлива рівність: INTEGRAL(u*dv) = uv – INTEGRAL(v*du)