Похідні основних елементарних функцій

Правила диференціювання

Похідна складеної функції Похідна оберненої функції

Похідна функції, заданої параметрично:

Питання №12

Похідна від функції заданої неявно, похідна від функції заданої параметрично.

Похідна від функції заданої неявно

1. Функція вважається заданою неявно якщо значення х та у повязані рівнянням F(x,y)=0

Зауваження: Терміни «явна» і «неявна» функція характеризують не природу функції а лише спосіб її задання

Для обчислення похідної для явно заданої функції((у)′) необхідно знати похідну від обох частин рівняння що задає функція, памятаючи , що х- змінна величина; у=у(х) функція від х. Із отриманого рівняння слід виразити шукану похідну у′

Зауваження Похідною від функції заданої неявно є функція задана неявно.

Похідна від функції заданої параметрично

функція називається заданою параметрично якщо значення х і у записані за допомогою деякого параметру t у вигляді такої системи

х =х(t)

y=y(t)

Питання №13

Похідна показниково-степеневої функції

Функція називається показниково - степеневою якщо вона має вигляд

у=(f(x))^(g(x)); f(x)>0

Нехай f(x) і g(x) диференційовані в точці х0 тоді для знаходження у ′ слід виконати наступні операції

у=(f(x))^(g(x))

ln у=ln (f(x))^(g(x))

ln у=g(x) * ln (f(x))^(g(x))

1\y*y′= g′(x)*ln(f(x))+g(x)*1\f(x)*f′(x)

y′=y*(g′(x)*ln(f(x))+(g(x)*f(x)) \ f(x)

y′=((f(x))^(g(x)))*(g′(x)*ln(f(x))+(g(x)*f(x)) \ f(x))

Питання №14

Два правила Лопіталя.

Розкриття невизначеностей при обчисленні границь

ТЕОРЕМА 1 (перше правило Лопіталя) нехай

1. неперервні на заданному інтервалі. Нехай ці функції задовольняють умові 1)

2)

3)

4)

ТЕОРЕМА 2 (друге правило Лопіталя) сформулювати аналогічно за умовою

Зауваження: Правила Лопіталяможуть бути застосовані повторно а також їх можна застосувати до невизначеностей іншої форми попередньо перетворивши їх до вигляду або Наприклад(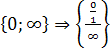

Питання №15

Схема дослідження функції за допомогою похідної.

Застосовуючи похідну першого та другого порядків, а також обчислення границь функції можна провести повне дослідження функції та побудувати її графік, загальна схема дослідження наступна:

1)ОДЗ- Область допустимих значень

2)Перевірка функції на наявність критичних точок, визначення інтервалів монотонності функції та точок екстремум ума( не забути знайти ординати критичних точок)

3)знаходження точки перетину функції та інтервалів опуклості функції (не забути обчислити ординати точок перегину)

4)Визначення асимптот (вертикальних, горизонтальних,похилих) графіка функції

5)З отриманими даними побудувати графік функції, знайшовши при необхідності точки перетину графіка з осями координат

Питання №16

Точка локального екстремуму , функції однієї змінної(Критичні точки та де їх шукати).

Критичні точки функції інтервали монотонності, точки екстремуму

1. Точка х0 є R називається точкою локального максимуму функції f: R ->R якщо

х є В( х0,δ) виконується f(х)<= f(x0)

Точка х0 називається точкою строгого локального max , якщо знак нерівності строгий для всіх , х ≠х0 аналогічно визн. точок локального min та строгого локального min f(х)= f(x0)

Точки локального min та max називаються точками локального екстремуму.

ТЕОРЕМА 1 нехай для функції f: R ->R точка х0 є точкою локального екстремуму тоді, якщо точка х0 існує f ′(x) то вона дорівнює 0

Зауваження згідно до даної теореми точки локального екстремуму для функції, щощо мають похідну слід шукати серед точок в яких f ′=0

2. Точки в яких похідна f ′=0 називаються критичними і стаціонарними точками даної функції

3. Функція f зберігає знак лівіше точки х0 якщо виконується одна із двох умов

1. ( х0-δ, х0 ) f(х)>0 або ( х0-δ, х0 ) f(х) <0

Аналогічно визначається поняття функції зберігає знак правіше х0 х є ( х0, х0+ δ )

ТЕОРЕМА 2 Нехай функція f: R ->R задовольняє умову х є ( х0, х0+ δ ) існує f ′(х) рпи чому х0 – критична точка f ′(х0)=0 і похідна f ′ зберігає знак правіше ті лівіше точки х0 тоді якщо при переході через х0 похідна змінює свій знак з + на - то точка х0 – точка локального максимуму.

тоді якщо при переході через х0 похідна функції змінює свій знак з – на + то точка х0 – точка локального мінімуму.

Якщо при переході через х0 похідна не міняє свій знак то точка х0 не є точкою локального екстремуму

Зауваження: Пригадаємо. що для зростаючої функції f(х), f ′>0, для спадної f ′<0

Питання №17

Інтервали випуклості та вогнутості функції, точки перегину

Дослідження інтервалів опуклості функції

1. функція f:(a,b)-> R Називається опуклою в гору на цьому інтервалі якщо графік функції f(a,b) лежить нижче будь-якої своєї дотичної.

2. функція f:(a,b)-> R Називається опуклою в низ на цьому інтервалі якщо графік функції f(a,b) лежить вище будь-якої своєї дотичної.

ТЕОРЕМА 1 Нехай функція f: R -> R двічі диференційована на інтервалі (a,b) тоді для того щоб функція f була опуклою вгору(вниз) необхідно і достатньо щоб

f ′ ′(х)<b(f ′ ′(х)>0)

3. Точка х0 називається точкою перегину функції f:(a,b)-> R якщо f неперервна в точці х0 на кожному із інтервалів ( х0-δ, х0 ) і ( х0, х0+ δ ) є (a,b) то функція опукла при чому напрямок опуклості різний

ТЕОРЕМА 2 Нехай f:(a,b)-> R х0 є (a,b) і х є В ( х0,δ) δ>0 f:(х). Нехай х0-точка перегину , тоді якщо f ′ ′(х) то f ′ ′(х)=0

ТЕОРЕМА 3 Нехай f:(a,b)-> R і х0 є (a,b) задовольняє умовам

1. δ>0 є В (х0, δ) f ′ ′(х)

2. f ′ ′(х)=0

3. f ′ ′- зберігає знак зліва і з права від точки х0, тоді х0- точка перегину якщо f ′ ′змінює знак при переході через х0 . х0 не є точкою перегину , якщо f ′ ′ не змінює свій знак при переході через х0

Питання № 18

Асимптоти графіка функції

Функція g(x)називається асимптотичне наближення функції f(x) якщо lim x->∞ (g(x))\(f(x))=1 або lim x->-∞ (g(x))\(f(x))=1

Асимптотою графіка функції однієї змінної будемо називати пряму, яка є асимптотичним наближенням графіка даної функції

Асимптоти бувають вертикальні, горизонтальні та похилі

1.Вертикальні асимптоти виникають там де функція має розрив. Нехай а-точка розриву функції f(x) пряма х=а буде вертикальною асимптотою графіка функції f(x)якщо точка а є точкою розриву 2-го роду

2.Для знаходження горизонтальних асимптот слід обчислити границі lim x->∞ f(x) і

lim x->-∞ f(x) якщо хоча б одна із границь має скінченне значення b то пряма у= b є горизонтальною асимптотою

3.Похилі асимптоти ( якщо вони існують у графіку даної функції ) – мають рівняння у=kx+b. Для знаходження коефіцієнта k слід обчислити дві границі lim x->∞ f(x) \ х і

lim x->-∞ f(x) \ х, якщо хоча б одна із границь дорівнює скінченому, не нульовому числу, то це число дорівнює k

Якщо знайдене число k≠0 то b= lim x->∞ [f(x)-k(x)] (i) або b=lim x->-∞[ f(x)-k(x)] (якщо ці границі існують і нескінченні)

Питання № 19

Диференціал функції, інваріантність форми першого диференціалу(правило обчислення складної функції - в кінці лекції)

Нехай f: [a;b] ->R f ′(x) x є [a;b]

За означенням f ′(x0)= lim ∆x->0 (∆f(х0))\(∆x0) очевидно що відношення (∆f(х0))\(∆x0) відрізняється від значення f ′(x0) на величину нескінченно малу відносно ∆x тобто

(∆f(х0))\(∆x0) = f ′(x0)+α(∆x) де α(∆x)- >0 при ∆x- >0 звідси слідує що

∆f(х0)= f ′(x0) *(∆x0) + α(∆x) *∆x при ∆x- >0 величина α(∆x) *∆x є величиною нескінченно малою 2го порядку, таким чином приріст функції ∆f(х0) в точці х0 складається з двох доданків 1го порядку малості і другого 2го порядку малості відносно ∆x. 1ший доданок називається головною частиною приросту функції.

1. Диференціалом функції називається головна частина приросту функції і позначається df(x0) df(x0)= f ′(x0)* ∆x

правило обчислення складної функції

Нехай h(x)=f(g(x)) складна функція де g(x) і f(x) мають похідні за ланцюговим правило f ′(x)= f ′(g(x))*g′(x)

Обчислемо диференціал від функції

h(x)*dh(x)=h′(x)*dx або

dh(x)= f ′(g(x))* g ′(x)*dx або

dh(x)= f ′(g(x))* d(g ′(x))

Порівнюючи праві частини двох останніх рівнянь легко бачити що вони мають одну і ту ж саму форму : похідна функції помножена на диференціал аргументу , тобто форма диференціалу не залежить від того чи є аргументом функції незалежна змінна чи функція іншого аргументу , ця властивість називається інваріантністю форми 1го диференціалу