Питання №1
Множина, алгебраїчні операції над множиною.
1. Множина-це сукупність сукупність об’єктів , що розглядаються у якості цілого. Об’єкти що скадають множину називаються її елементами. Множина називається заданою, якщо відома ознак притаманна всім елементам цієї множини або перелічені всі елементи цієї множини.
Позначення:A,B,C,D … -множина, a1,a2…- елементи множини А, А={a1,a2…}
Множини бувають скінченними і нескінченними
Нескінченні множини можна розділити на два класи – зліченні і незліченні
Зліченними називають множини, елементи яких можна занумерувати(Неперервні)
2. Множина, яка не містить жодного елементу називається порожньою Позначається ø
Нехай А={a1,a2…}, B={b1,b2…}
3
.
В А(підмножина)
х є В ->х є А
З ауваження ø А, А
4. А=В(рівність множин)
Я кщо А В і В А
5
.
А В( претин множин)
А
В={х: х є А і х є В},
6
.
А В(обєднання множин)
А В={х: х є А або х є В},
7. А\В(різниця двох множин)
А\В={х: х є А і х Ɇ В},
8 . А(не А доповнення до множини А)
А = {х: х Ɇ А },
Нехай Х і У дві множини
9. Відображенням (функції ) f множини Х в множину У називається правило яке кожному елементу х є Х ставить у відповідність тільки один елемент у є У
f:
х є Х
!
у=
f(х)єУ
Питання №2
Загальне поняття функції.
1. Відображенням (функції ) f множини х в множину у називається правило яке кожному елементу х є х ставить у відповідність тільки один елемент у є у
f: х є Х ! у= f(х)єУ
Слова: функція, відображення, відповідність, перетворення, оператор є синонімами позначення
Позначення f:Х->У, у= f(х), х є Х
Істрично функції походить від латинського – виконувати
Термін функція і позначення у= f(х) х є Х вперше застосував Лейбніц.
Елемент у який перетворення f ставить у відповідність елементу Х називається образом елемента х при відображенні f або значенням функції f в точці х.
Множина Х називаєть множиною визначення функції f і позначається D(f)
Множина R(f)={y: x є D(f) і у= f(х) } називається множиною значення функції f
2. Нехай f:Х->У графіком функції f називається множиною G(f)={(x,y):x є X, y= f(х)}
G (f) X xY
3. Нехай f:Х->У, g:Y->Z функція h:X->Z як визначається h(x)=g(f(x)), x є Називається складною функцією або суперпозицією функції g і f. h(x)=g(f(x)),
4. Відображенням
f:х->у
називається взаємооднозначним
відображенням множини х в множину у
х1
є х ,
х2
є х: х1 
х2
виконується f(х1)
f(х2)
5. Нехай f:х->у-
взаємо однозначне відображення тоді
у
єУ
х є Х: f(х)=у
Покладемо 
Функція 
називається
називається оберненою до функції 
Надалі будемо
розглядати функції 
(дійсна
функція дійсного аргументу)
6. Коренями функції у= f(х) називаються корені рівняння f(х)=0
Графічно корені функції це абсциса точок перетину графіку функції з віссю Ох.
7. Множина 
і 
називається інтервалами знаку сталості
функції
у= f(х)
8. Нехай х0 є R
, 
( ебсілон називається довільне додатнє
число , як завгодно мале )
Околом або 
точки х0 – називається інтерва 
Питання №3
Числова послідовність, границя числової послідовності.
Відображення f: N->R називається послідовність дійсних чисел
Позначається{an:n>=1}={a1,a2,a2,a3...an...}
Де an=f(n)називається загальним членом послідовності.
2. Послідовність {an:n>=1}називається обмеженою якщо існує с є R якщо для всіх n>=1,(an)<=c
3. Число а є R називається границею числової послідовності {an:n>=1} якщо ε>0, N(ε) n>N(ε) виконується | an - a |< ε
Позначення
при an
-> a,
n->∞
Говорять що послідовність an- збіжна а або an має границю а
Якщо послідовнісь границі не має то таку послідовність називають розбіжною
ТЕОРЕМА 1 Послідовність дійсних чисел може мати тільки одну границю
4.
Послідовність
називається
Нескінченно
великою,
якщо, яке б не було число
,
існує таке число
,
що для всіх
виконується
нерівність
.
Питання №4
Властивості збіжних послідовностей.
1. Збіжна послідовність обмежена.
2. Нехай для послідовності {an:n>=1}{bn:n>=1}{сn:n>=1} виконуються умови
n>=1; Cn<=an<=bn
Cn->a; bn->a ;n->∞ тоді
3.
Нехай послідовності
і
–
збіжні, при цьому
.
Тоді збіжні й послідовні
(
- стала),
(остання
при
),
причому:
1) 
2) 
3) 
4) 
4. Послідовність {an:n->1}називається монотонно зростаючою якщо для будь-якого n>1 виконується an<an+1
Послідовність {an:n->1}називається монотонно неспадною якщо an<=an+1
Послідовність {an:n->1}називається монотонно зростаючою якщо для будь-якого n>=1 виконується an>=an+1
Послідовність {an:n->1}називається монотонно зростаючою якщо для будь-якого n>=1 виконується an>an+1
Послідовність із будь-яких чотирьох вище зазначених типів називається монотонною
Теорема 2 Монотонно обмежена послідовність дійсних чисел є збіжною
Питання№5
Границя функції
Нехай f:R->R
1. (Означення границі функції по Коші)Нехай x0 є R ,число p є R називається границею функції в точці x0, якщо ε>0, δ (ε)=δ>0, x є |x-x0|<δ виконується |f(x)-p|< ε
2. (Означення границі функції по Гейне) Нехай f:R->R
число р називється грницею функції в точці х0, якщо послідовності {хn:n>=1} така, що
n>=1,хn ≠х0 і lim x->∞ (xn)=x0 і Виконується lim n->∞( f(xn))=p
Означення границі функції по Гейне і по Коші еквівалентне
По Гейне По Коші
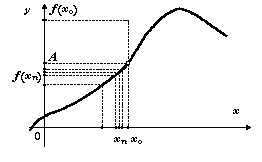
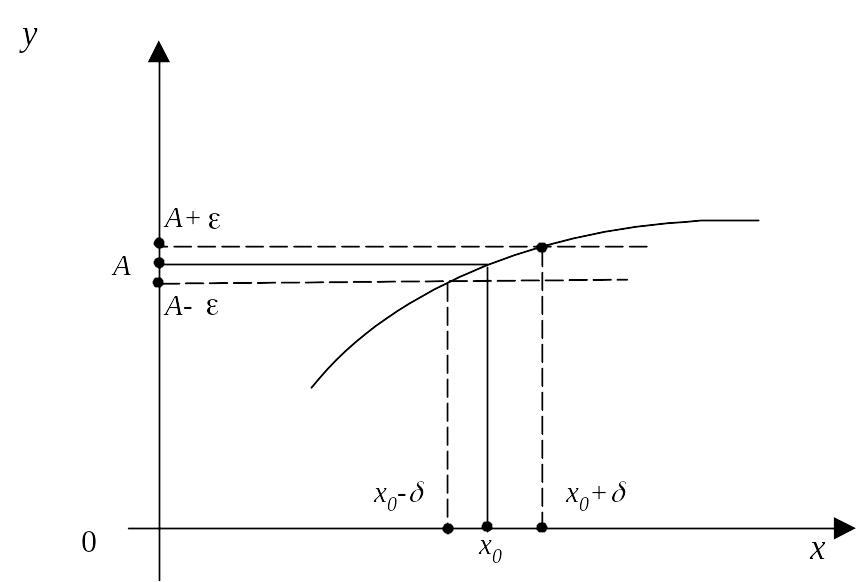
Позначення lim х->х0( f(x))=p
якшо х0 є ∞
Говорять що lim х->х0( f(x))= ∞, якщо с є R; x є |x-x0|< δ; f(x)>c
lim х->х0( f(x))= -∞, якщо с є R; x є |x-x0|< δ; f(x)< c
В першому випадку функція називається нескінченно великою при х->х0
Якщо функція така, що lim х->х0( f(x))= 0, то вона називається нескінченно малою
Питання №6
Властивості границі функції в точці
1. Функція в даній точці може містити тільки одну границю
2. lim х->х0(с f(x))= с lim х->х0( f(x)) с є R
3. lim х->х0(f(x)+ g(x))= lim х->х0( f(x)) + lim х->х0( g(x))
4. lim х->х0(f(x) * g(x))= lim х->х0( f(x)) * lim х->х0( g(x))
5. lim х->х0(f(x) \ g(x)) = lim х->х0( f(x)) \ lim х->х0( g(x)); lim х->х0( g(x)) ≠0
6. lim х->х0(f(x))^n= (lim х->х0(f(x)))^n, n є N
7. lim х->х0((sqrt n)*(f(x))) = (sqrt n)*(lim х->х0 (f(x)))
8. lim х->х0(a^f(x))= a^ lim х->х0(f(x); a>0;a≠1
9. lim х->х0(ln f(x))= ln lim х->х0(f(x))
10. lim х->х0((f(x))^g(x))= (lim х->х0((f(x)))^ (lim х->х0(g(x))
При знаходженні границі функції в точці важливо знати
1. слід значення х0 підставити у функцію для якої шукаємо границю, якщо отримане значення с скінченне число то це число і є шуканою границею.
2. При підстановці х0 у функцію можуть бути отримані невизначеності різних видів розглянемо деякі із них
{∞\∞} виділяємо нескінченно малі доданки та відкидаємо їх як такі. що не впливають на значення границі
{∞ - ∞} звести невизначеність до форми {∞\∞} шляхом зведення до спільного знаменника доповненням до різниці квадратів або різниці кубів
{0\0} слід скоротити дріб на вираз( х-х0)
У випадку відношення многочленів чисельник та знаменник розкладаються на множники при необхідності використовувати метод ділення многочлена на многочлен в стовпчик
У випадку ірраціонального дробу слід позбавитися ірраціональностей у чисельнику та знаменнику шляхом використання формул скороченого множення
Якщо чисельник і ( або)знаменник містить тригонометричні показникові функції то слід скористатися таблицями еквівалентності нескінченно малих величин
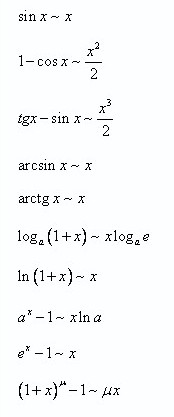
t
0 Зауваження:
Особливу увагу слід звернути,що аргумент функції. які входять до таблиці еквівалентностей має прямувати до 0 тому при таму при необхідності слід використовувати заміну змінної
2. перша еквівалентність у таблиці
sin t ~t - отримана за допомогою першої важливої границі
{1^∞}-зводиться до другої важливої границі
або
Питання №7
Нескінченно малі величини, таблиця еквівалентності нескінченно малих, Друга важлива границя.
Послідовність
називається нескінченно малою, якщо
. Наприклад, послідовність чисел
— нескінченно мала.
Це ж означення можна викласти і в іншому формулюванні. Послідовність називається нескінченно малою, якщо вона по абсолютному значенню стає і залишається меншою як завгодно малого наперед заданого числа ε > 0, починаючи з деякого місця.
Жодне число окрім нуля не може бути віднесене до нескінченно малих величин.
Властивості нескінченно малої
Алгебраїчна сума декількох нескінченно малих величин є також величина нескінченно мала
Різниця двох нескінченно малих величин є величина нескінченно мала
Добуток обмеженої змінної величини на нескінченно малу є величина нескінченно мала
Відношення двох нескінченно малих величин не обов’язково є величина нескінченно мала
Границя нескінченно малої
Постійне число а
називається границею послідовності
,
якщо різницею між ними є нескінченно
мала величина.
Інші означення нескінченно малої
Функція називається
нескінченно малою в околиці точки ,
якщо
.
Функція називається
нескінченно малою на нескінченності,
якщо
або
.
Також нескінченно
малою є функція, що являє собою різницю
функції і її границі, тобто якщо є
,
то
,
.
t -> 0 {1^∞}-зводиться до другої важливої границі
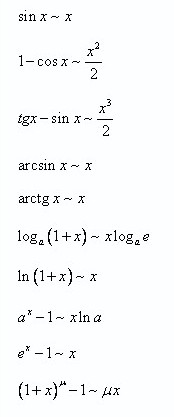
або
Вважається,
що
,
оскільки функція не визначена при цих
аргументах, факт існування цієї границі
приймемо без доведення.
Питання№ 8
Неперервність точок в функції, класифікація точок розриву.
Нагадаємо що нехай x0 є R ,число p є R називається границею функції в точці x0, якщо ε>0, δ (ε)=δ>0, x є |x-x0|<δ виконується |f(x)-p|< ε
1. число а є Rназивається границя з ліва функції в точці х0 якщо ε>0, δ=δ(ε )>0, x є |x0-δ, x0| виконується |f(x)-p|< ε
Позначається lim х->х0- ( f(x))
2. число а є Rназивається границя з ліва функції в точці х0 якщо ε>0, δ=δ(ε )>0, x є |x0, x0+δ | виконується |f(x)-p|< ε
Позначається lim х->х0+ ( f(x))
Очевидно, що lim х->х0 ( f(x)) існує якщо lim х->х0- ( f(x))= lim х->х0+ ( f(x))
3. Функція f:R->R називається неперервною в точці х0, що належить R якщо
lim х->х0- (f(x))= lim х->х0+ ( f(x))= f(x0)
Якщо порушується хоча б одна із рівностей(3) то функція називається розривною у точці х0
Класифікація точок розриву
4. Якщо lim х->х0- (f(x))= lim х->х0+ ( f(x)) ≠ f(x0) то така точка х0 називається точкою усувного розриву
5. Якщо обидві границі lim х->х0- (f(x))= lim х->х0+ ( f(x)) існують. і скінченні тобто
lim х->х0- (f(x))= a<∞; lim х->х0+ ( f(x))=b<∞; a≠b то точка х0 називається точкою розриву 1го роду при цьому говорять що функція в точціх0 має скачок величина якого w=b-a
6. Якщо хоча б одна із границь не існує або дорівнює + або - ∞ то точка х0 називається точкою розриву 2го роду
7. Функція f:R->R називається неперервною на інтервалі (а,b) є R якщо вона неперервна в кожній точці цього інтервалу.
ТЕОРЕМА
Нехай функція f:R->R розглядається тільки на скінченному закритому інтервалі [a;b] ((f:[a,b]->R]) f- монотонна) тоді на цьому інтервалі в якості точок розриву можуть бути тільки скачки
Питання №9
Елементарні властивості неперервних функцій.
1. Нехай f:R->R неперервна точці f(x0) тоді складна функція g( f(x)) неперервна в точці х0( теорема про неперервність складної функції)
2. (Перша теорема Вейлерштраса) Функція f:R->R неперервна на відрізку [a;b] обмежена на цьому відрізку
3. .(Друга теорема Вейлерштраса) Функція неперервна на відрізку приймає на цьому відрізку своє найбільше і найменше значення.
4. Якщо f(x) неперервна на відрізку [a;b] і f(а) та f(b) різних знаків то існує х0 є [a;b],
f(x0)=0
Питання №10
Похідна функції в точці, фізична і геометрична інтерпретація похідної.
Основні поняття
Нехай f:R->R визначена в деякому околі точки х0. Покладемо∆х=х-х0, х ≠х0
∆f(x)=f(x)-f(x0)=f(x0+∆x)-f(x0)
1. Якщо існує скінченна границя відношення приросту функції до приросту аргументу при умові, що приріст аргументу нескінченно малий то ця границя називається похідною функція в даній точці y′ =. lim х->х0(( f(x0+∆x)- f(x0)) \ ∆x)
Позначення f′ (x0); df(x) \ dx
Фізична та геометрична інтерпретація похідної
Нехай точка Р рухається по числовій прямій позначимо через s(t)координату точки Р в момент часу t. Нехай t1,t2- 2вамоменти часу (t1<t2) Очевидно, що середня швидкість точок за період часу [t1,t2] визначається відношенням (s(t2)- s(t1))/ (t2 -t1), де s(t2)- s(t1)- шлях що пройшла точка Р за час t2 -t1. Миттєву швидкість точки Р в момент часу t1 можна визначити як lim t2-> t1+ (s(t2)- s(t1))/ (t2 -t1),
Розглянувши останню рівність і записавши її у вигляді як lim ∆t-> 0+ (s(t1+∆ t)- s(t1))/∆t
визначається як похідна функції s(t1)
vт(t1)= s′(t1)
Якшо відома миттєва швидкість матеріальної точки в момент часу t то значення s цієї точки можна приблизно визначити як s′(t)* ∆t
Геометрична ітерпритація
Нехай f: (а,b) ->R і х0 є (а,b) пряма що проходить через точки Р0(х0;f(x0)) і Р0(х;f(x)) для
х ≠х0 називається січною до графіка функції f(x) положення січна визначається ∠ нахилу α (відраховується від додатнього на прямій осі ОХ проти годинникової стрілки) та точки Р.
Тоді із малюнка легко визначити tg кута нахилу січної tg α= (f(x)- f(x0))/ x-х0
При цьому значенні ∠α є( - π\2;π\2]
Якщо х->х0 то Р->Р0 переміщуючись по графіку функції f(x). Очевидно, що січна буде змінювати своє положення (змінюється∠α)наближаючись до певного граничного положення, якщо це граничне положення існує при Р->Р0 то при нескінченному наближенні Р до Р0 січна перетворюється на дотичну до графіка функції f(x) в точці Р0 , а
α-> α0 -кут нахилу дотичної в даній точці
Зауваження: дотичної в деякій точці може не існувати
ТЕОРЕМА : дотична до графіку функції в точці(х; f(x0)) або(кут нахилу α0) існує тоді і тільки тоді коли існує похідна f ′(x0) При цьому
f ′(x0)= tg α0= lim ∆х-> 0+ (f (х0+∆х)- f (х0))/∆х
α - кут нахилу дотичної
Зауваження 1: Означення похідної функції в точці має локальний характер, тобто поведінка( f(x)- f(x0)) \ х-x0); х ≠х0не змінюється, якщо за межами околу точки х0 довільно змінюється значення функції
Зауваження 2:Рівняння дотичної в даній точці можна записати виходячи з означення похідної f(x)- f(x0)= f ′(x0)( x- x0) або y′ =.y0+ y′ (x0)( x- x0)
Зауваження 3:Якщо в точці х0 існує функція f ′(x0)то функція f (x) є неперервною в точці х0
Обернене твердження невірне тобто неперервна в точці х0функція може не мати в цій точці похідної( графічно точки ізлому)
Питання №11
Правило обчислення похідних, таблиця похідних.
Якщо х існує f ′(x) то операція обчислення функції f ′ називається диференціюванням функції f
Властивості
Правила обчислення похідних
1. Нехай функція f:R->R і g:R->R мають похідні f ′(x0) і g ′(x0)в точці х0 тоді:
1. с є R функція с f(х) має похідну в точці х0 і (с f)′ (х0)= с*f′ (х0)
2. Функція f + g має похідну в точці х0 і (f + g )′(х0)= f ′(х0)+ g ′(х0)
3. Функція f * g має похідну в точці х0 і (f * g ) ′ х0)= f ′(х0)*g (х0)+ f (х0)*g ′(х0)
4. Якщо g (х0) ≠0 то функція f / g має похідну в точці х0 і
(f / g) ′(х0)= (f ′(х0)*g (х0)- f (х0)*g ′(х0)) g ^2(х0)
2. Правило диференціювання складної функції або ланцюгове правило:нехай функція
f:R->R має похідну f ′(x0) в точціх0а функція g:R->R має похідну в точці у0=f (x0) тоді [g(f(x0))] ′ = g ′(f (x0))* f ′(x0)
Таблиця похідних основних і елементарних функцій