21. Методы упрощения сложных систем. Быстрые, средние, медленные времена.

_{Быстрые, средние и медленные времена}

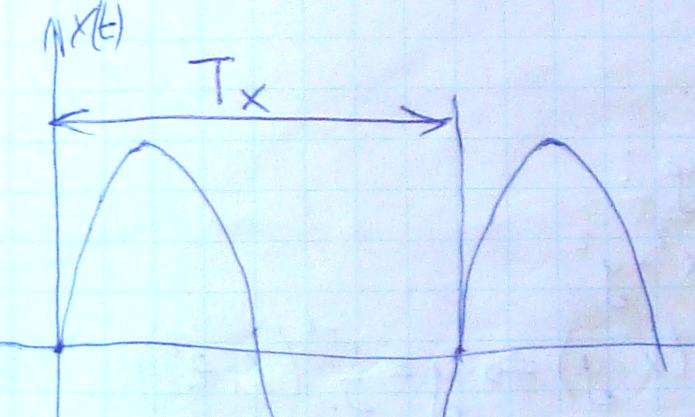
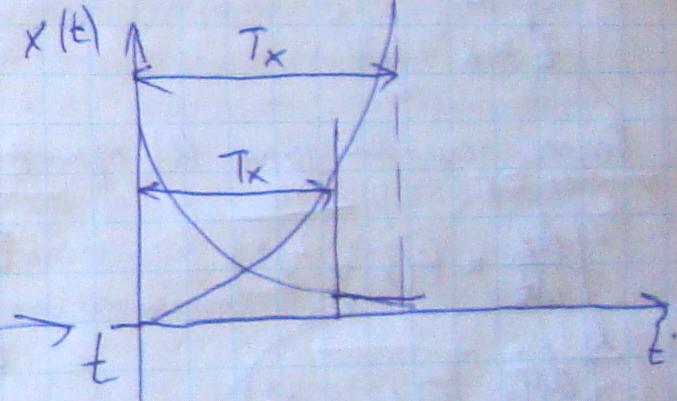
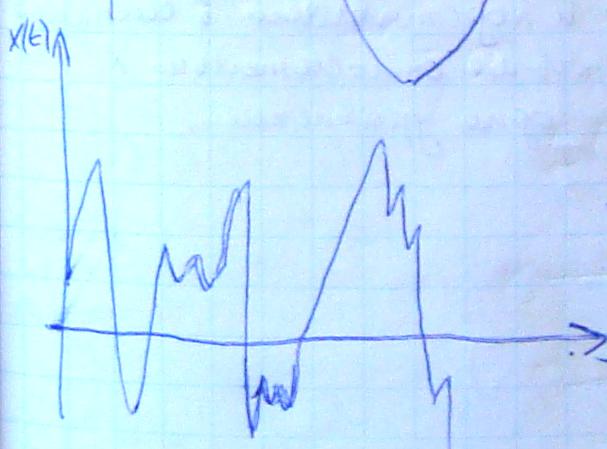
_{dx/dt=P(x, y, z) Tx – характерное время изменения x}

_{dy/dt=Q(x, y, z) Ty - характерное время изменения y}

_{dz/dt=R(x, y, z) Tz - характерное время изменения z}

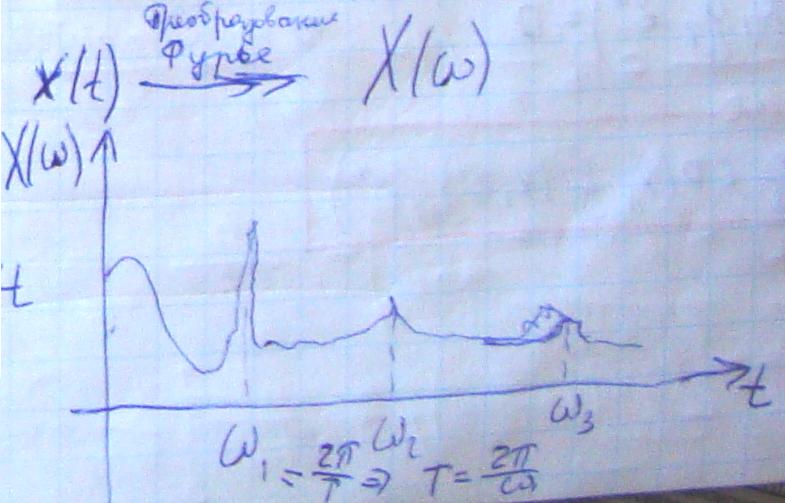
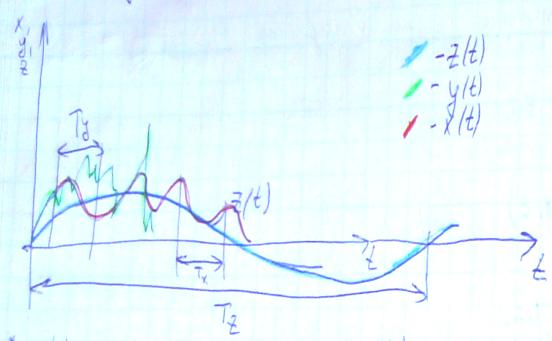
_{Пусть Tx ~Ty (сравнимы м/у собой). Tx,Ty<<Tz}

_{z(t)=const=z*, то dz/dt=0, R(x,y,z*)=0}

_Н-р:

22. Модель всплеска численности популяции.

Модель вспышки численности популяции

Примером практической модели, демонстрирующей 2 линейно устойчивых стационарных состояния популяции является модель следующего вида:

где r_B – характеризует линейный рост численности популяции,

К_В - характеризует емкость среды, которая зависит от плотности распределения пищи

p(N) – выражает истребление элементов популяции, в основном за счет их поедания хищниками

К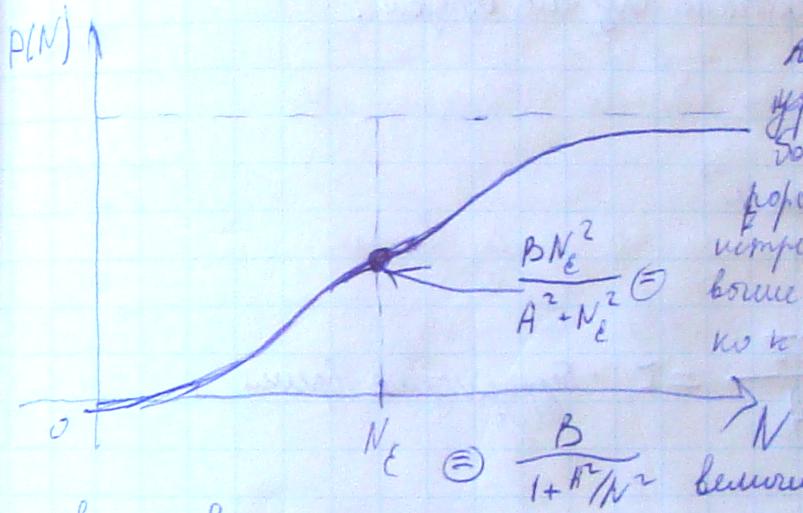 ачественно зависимость p(N) выражается следующим образом: рис.

Истребление обычно достигает уровня насыщения при достаточно больших N. Существует определенно пороговая величина N_ε, ниже которой истребление мало, в то время как выше этой величины истребление близко к уровню насыщения. Такая функциональная модель подобна переключателю, где N_ε – это критическая величина, соответствующая в некотором смысле переключения.

A и В – положительные константы, тогда динамика численности популяции N(p) определяется следующим уравнением:

Это уравнение имеет 4 параметра: r_B, K_B, A, B. При этом коэффициенты А и К_В имеют такую же размерность как и N, коэффициент [r_B]=

Коэффициент В имеет размерность [B]=

А – величина порога, при которой включается истребление. Если величина А мала, то порог тоже мал.

При моделировании часто бывает удобным привезти модель к базисному виду. Данная операция часто дает исследованию ряд преимуществ. Н-р, используемый в ходе анализа единицы измерения после приведения к безразмерному виду становится неважным и можно привезти сопоставление «больших» и «малых» характеристик систем. К тому же в результате этой операции всегда происходит числа значимых параметров, определяющих динамику системы. Здесь введем безразмерную величину следующим образом

A₁=1 м^-3, А₂=150 м^-3, А₃=10000 м^-3

, – безразмерное время

Процесс приведения к безразмерному виду:

Полученное уравнение (1) имеет только 2 параметра r и u, которые являются безразмерными величинами. В данном случае u<<1 означает что N<<A. В реальных переменных это означает, что истребление при данной численности можно пренебречь. В любой модели обычно существуют несколько разных возможностей приведения к безразмерному виду.

Стационарное состояние уравнения (1) является решением следующего уравнения

(2)

=> 1) u=0

2) (3)

(лк №18)

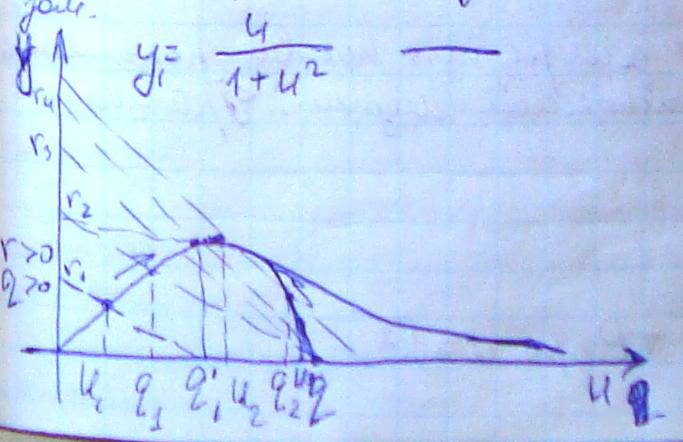
Наименьшее решение уравнения (3) удобнее определить графически следующим образом

; ;

Это один из способов решения систем. Надо исследовать устойивые или неустойчивые стационары. Для этого надо их линеаризовать.

И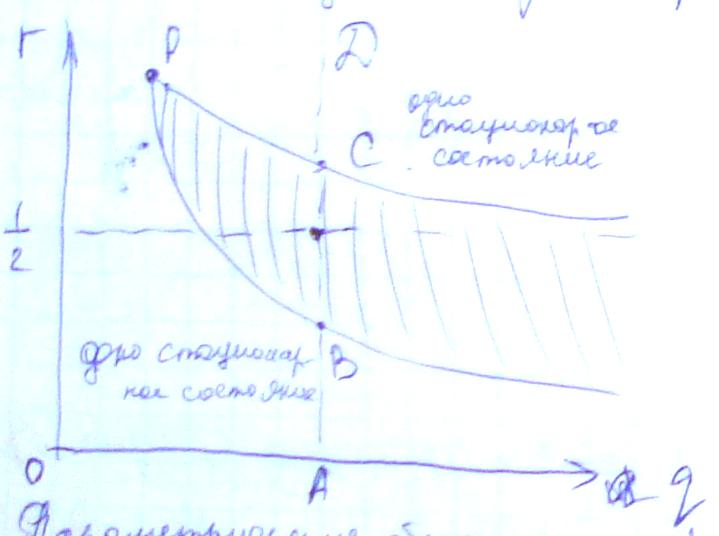 з данного рисунка следует что существует область значений параметров r и q, где уравнение (3) имеет 3 корня.

Данная модель т.о. демонстрирует эффект гистерезиса

Параметрические области существования для разного количества положительных стационарных состояний рассматриваемой модели. Граничные кривые заданы параметрически

Пусть мы имеем фиксированную величину q и пусть r возрастает от 0 вдоль линии ABCD, при этом q=A, тогда если q₁=0 (стационарное состояние) при r=0, то значение u₁ монотонно возрастает с ростом r до тех пор, пока не будет достигнута точка С. При более высоких значениях r это стационарное состояние исчезает и система перескакивает в другое равновесное состояние в точку u₃. Если уменьшать параметр r, то система останется в положении u₃ до тех пор, пока r не достигнет нижней критической величины, где опять будет существовать только одно стационарное состояние и оттуда произойдет перескок из u₃ в состояние u₁.

Другими словами по мере роста r вдоль ABCD происходит скачок вверх в т.С, в то время как при уменьшении r от D до А происходит скачок вниз в т.В. Это пример возникновения катастроф в системе.