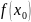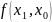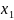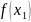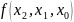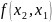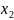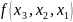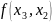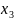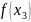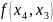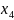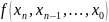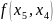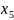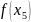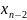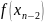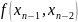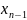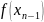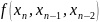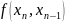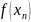Неявний Чебишевський ітераційний метод

Швидкість збіжності явного методу (2) і чим більше 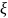тим вища швидкість збіжності методу.

(1) , 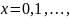- початкове наближення

У (1) В є симетричною і доатньовизначеною 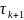є змінним і залежить від номера ітерації.в данному випадку швидкість збіжності методу буде залежною від .

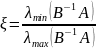Теорема_2

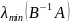
Нехай А, В симетричні додатньовизначені матриці це відповідні найменше і найбільше власне значення матриці і нехай відомо число ітерацій m, тоді метод має мінімальну похибку 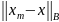, якщо параметри визначаються наступним чином

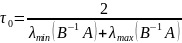, , , (17)

,

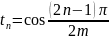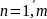
І при цьому буде справедлива оцінка

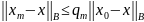(18) де ,

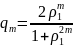В теоремі_1 і теоремі_2 в нас відомі точні границі спектрів матриць. Але часто в таких задачах дуже важко знайти спектр матриці, але є відомими оцінки:

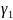
(19) де 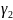= const>0 , тоді

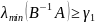
Тоді якщо виконується (19) то справедлива теорема.

Теорема

Нехай матриці А і В симетричні і додатньовизначені, і для них виконується умова (19) і нехай задане число ітерацій m, якщо параметри будуть визначатись з рівностей

, , ,

То для похибки буде справедлива оцінка )

де ,

Інтерполяція функцій

Постановка задафі інтерполяції: Нехай задана функція 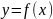визначена на проміжку [a,b] в деяких точках

, , … ,

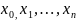
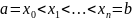
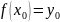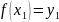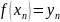
Треба побудувати 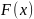, яка буде належати до деякого визначеного класу функцій і в точках прийме ті ж значення, що і 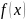,тобто

, , ….,

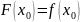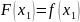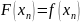
Точки 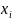– вузли інтерполяції.

Задача інтерполювання алгебраїчного многочлена

У просторі 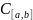вибрана скінченна множина функцій 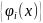. Функції 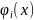є такими що довільний скінченний набір є лінійно незалежний, і тоді інтерполяційний многочлен, який у вузлах інтерполяції співпадає із значеннями функції у вузлах будемо шукати у виді

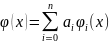(1)

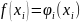
Тоді в якості функцій можемо вибирати наступні функції

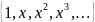
Так як у нас виконується умова близькості, тоді

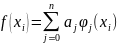(2)

Рівність (2) представляє собою систему алгебраїчних рівнянь, з якої необхідно знайти параметри

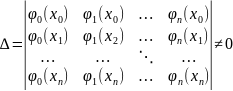
Такий набір функцій при якому 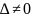називається система функцій Чебишева. 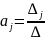, де – це детермінант матричної системи в якому вектор замінений вектором вільних членів

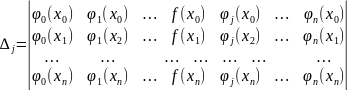
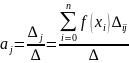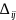Тобто , де - мінор

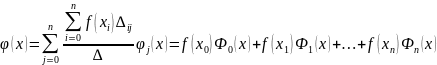
Де

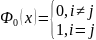
Інтерполяційний многочлен Лагранжа

В якості базисних функцій будемо вибирати систему функцій і тоді детермінант буде мати вигляд

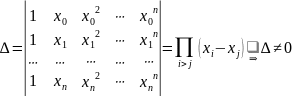
Тоді інтерполяційний многочлен буде шукатися у виді:

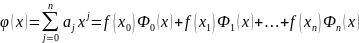(3)

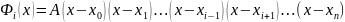
Всі вузли інтерполяції крім 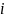-го є коренями даного многочлена тоді врахувавши, що

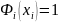
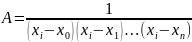
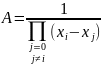тоді функція 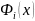запишеться

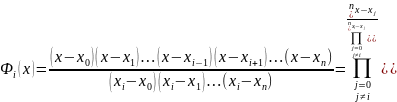(4)

Підставимо (4) у (3)

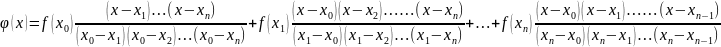
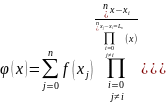
Розділені різниці. Інтерполяційний многочлен Ньютона

Нехай задана деяка функція 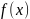яка визначена в своїх точках , ,

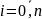
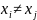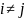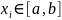
Розділена різниця першого порядку називається відношення

………………………………

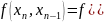
По розділених різницях першого порядку ми можем побудувати розділені різниці другого порядку

………………

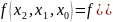
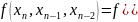
Розділені різниці 𝑛 – го порядку можна записати через розділені різниці 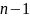порядку

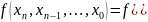
Розділені різниці зручно записувати у таблиці

				…
				…
					…
				…
				…
					…
…		…	….	…
				…