
- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Модифікація методу Гауса
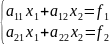
Якщо
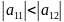 ,то в
подальшому будемо розглядати систему
,то в
подальшому будемо розглядати систему

Така
модифікація називається модифікацією
методу Гауса з вибором головного елемента
у рядку. В ролі головного елемента буде
виступати
 .
.
Якщо
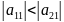 , то будемо розглядати систему
, то будемо розглядати систему
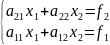 головний
елемент -
головний
елемент -

Цей метод відповідає за пере нумерування рядків у даній системі.
Метод Гауса з вибором головного елемента по всій матриці:

Тоді формально метод зводиться до перестановки рядків і стовпців.
Підрахуємо кількість операцій множення і ділення,які виконуються у ході методу Гауса.
Обчислимо кількість операцій ділення коефіцієнта матриці С

Обчислимо
кількість операцій множення для
обчислення коефіцієнта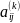
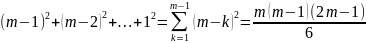
Таким
чином для обчислення елементів матриці
С необхідно виконати таку кількість
операцій

При достатньо великих m.
При
обчисленні
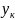 у формулі (14) буде виконуватись ділення,
а для знаходження
у формулі (14) буде виконуватись ділення,
а для знаходження
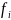 формули
(14) буде виконуватись
формули
(14) буде виконуватись
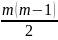 дій множення і ділення.
дій множення і ділення.
При
прямому ході методу Гауса буде виконуватись
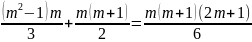
Для обчислення оберненого ходу методу Гауса ми будемо виконувати таку кількість операцій множення:

Для
виконання всього методу Гауса здійснюються

Тоді
в середньому для обчислення значень
однієї невідомої можемо прийняти
 дій.
дій.
Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
Розглянемо систему (1) яку ми зводили до вигляду (2), де с-матриця діагональна з одиницями на головній діагоналі. Випишемо формули, які зв’язують
 k=1,…,m
k=1,…,m
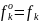 (3)
(3)
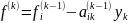 (4)
(4)
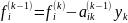 (5)
i=k
(5)
i=k
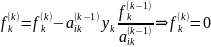
Покладемо і=1 к=1
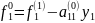

К=2 і=1
У рівності (5) поставимо і=2 к=1
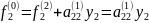
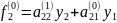
і=3 к=1
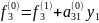
і=3 к=2
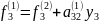
і=3 к=3
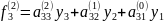
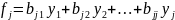 (6)
де
(6)
де
 (7)
(7)
f=By
(8)
 - матриця
з нулями вище головної діагоналі
- матриця
з нулями вище головної діагоналі
Враховуючи нерівність (7) запишемо матрицю В через:
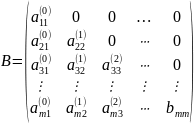
Діагональні елементи матриці В є ті елементи,які за припущенням методу Гауса не дорівнюють 0.
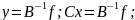 BCx=f;
тоді
А=В-С;
BCx=f;
тоді
А=В-С;
Розклад матриці А на добуток двох матриць називається факторизацією. Тоді метод Гауса може бути зведений до розв’язування системи
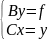 (9)
(9)
Розклад матриці на добуток відповідного прямого ходу методу Гауса,а розв'язок системи (9) – зворотному.
А=LU (10)
Позначимо - мінори
j-го
порядку матриці А.
- мінори
j-го
порядку матриці А.

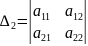
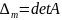
Тоді обґрунтованість розкладу матриці А на добуток двох матриць виражається теоремою.
Теорема:
Нехай всі мінори матриці А .Тоді
матриця А може бути представлена,причому
єдиним способом у вигляді добутку (10),
де L
– нижня трикутна матриця з не нульовими
діагональними елементами, U
– верхня трикутна матриця.
.Тоді
матриця А може бути представлена,причому
єдиним способом у вигляді добутку (10),
де L
– нижня трикутна матриця з не нульовими
діагональними елементами, U
– верхня трикутна матриця.
Доведення: Доведення проведемо методом математичної індукції. Перевіримо виконання умови теореми для матриці 2 – го порядку.

Елементи
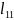 ,
,
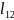 ,
,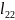 ,
,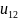 - невідомі.
- невідомі.
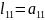
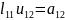
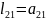

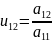
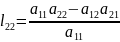

Припускаємо,що теорема справедлива для матриці А к-1 порядку. Переконаємось,що теорема виконується при к-му порядку матриці А.
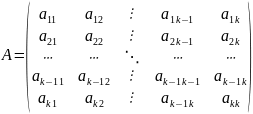 (11)
(11)
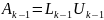
Ці матриці мають властивості,вказані в теоремі.
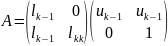 (12)
(12)
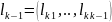

Перемножимо
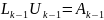 (13)
(13)
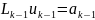 (14)
(14)
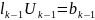 (15)
(15)
 (16)
(16)
Із припущення
індукції випливає
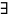 обернена матриць
обернена матриць
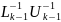 , тоді із (14)(15)
, тоді із (14)(15)

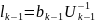
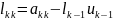
Таким чином ми
показали що LU
розклад існує. Покажемо, що det
k-
го порядку
 0
0
detA=det
Покажемо єдність:
Припустимо що є
два розклади
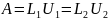 . Якщо
виконується така рівність
. Якщо
виконується така рівність
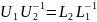 ми маємо
добуток двох діагональних, то це може
виконуватись у випадку, коли зліва і
справа є одинична матриця, тоді
ми маємо
добуток двох діагональних, то це може
виконуватись у випадку, коли зліва і
справа є одинична матриця, тоді
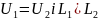 тобто розклад є єдиним.
тобто розклад є єдиним.
Зауваження: при застосуванні методу Гаусса необхідно перевірити відмінність від нуля кутових елементів. Так, як рівність одного з них нулю приводить до неможливого LU розкладу, а відповідно до застосування методу Гаусса.
